5.5. Свойства функций, непрерывных на отрезке

Теорема 1(Вейерштрасса): Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.

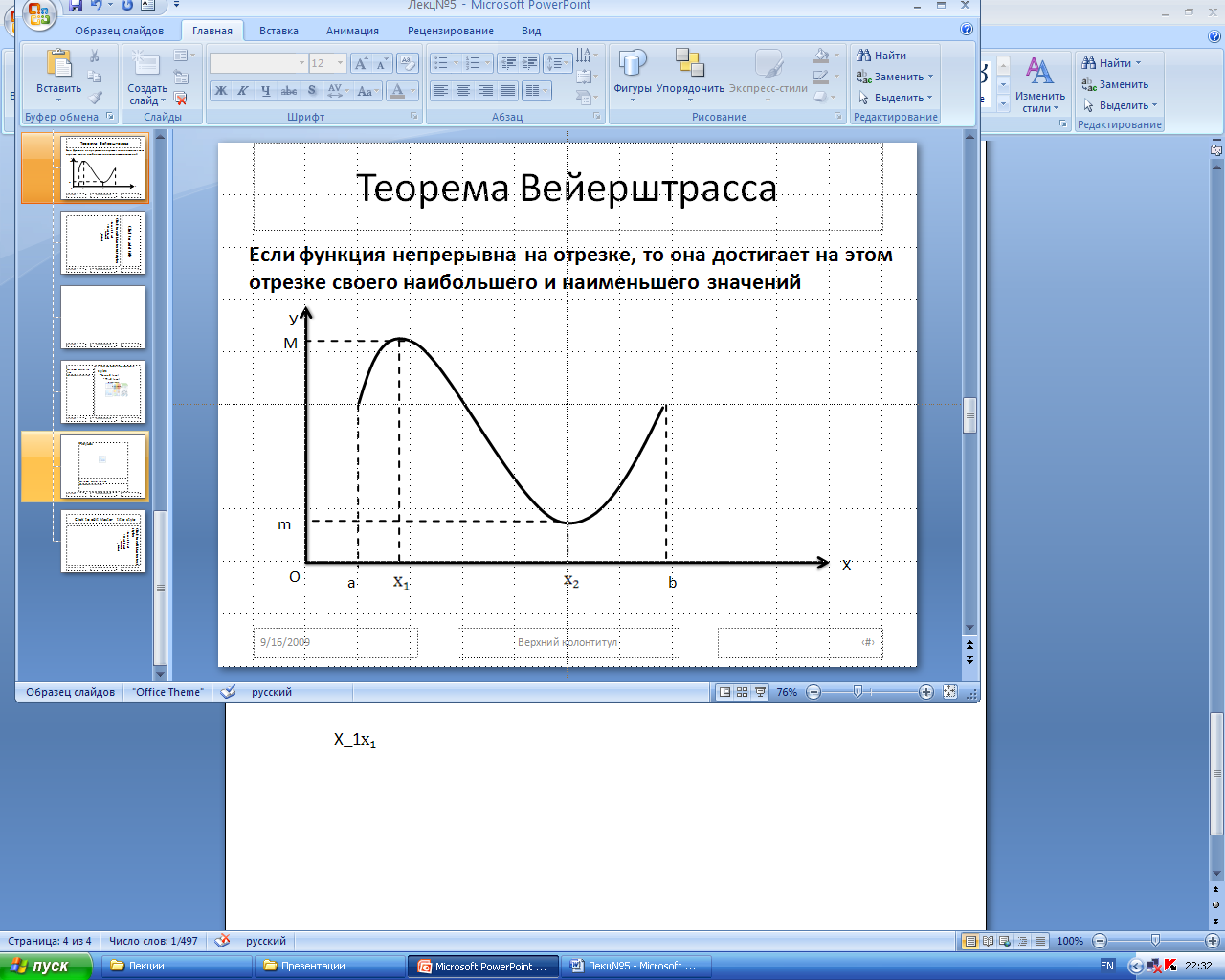
Изображенная на рисунке функция принимает свое наибольшее значение М в точке , а наименьшее значение m в точке . Для любого значения имеет место неравенство: .

Теорема 2( Больцано- Коши): Если функция y=f(x) непрерывна на отрезке и принимает на его концах неравные значения f(a)=A, и f(b)=B, то на этом отрезке она принимает все промежуточные значения между А и В.

Следствие: Если функция y=f(x) непрерывна на отрезке и на его концах принимает значения разных знаков, то внутри отрезка найдется хотя бы одна точка с, в которой данная функция f(x) обращается в нуль : f( c)=0.

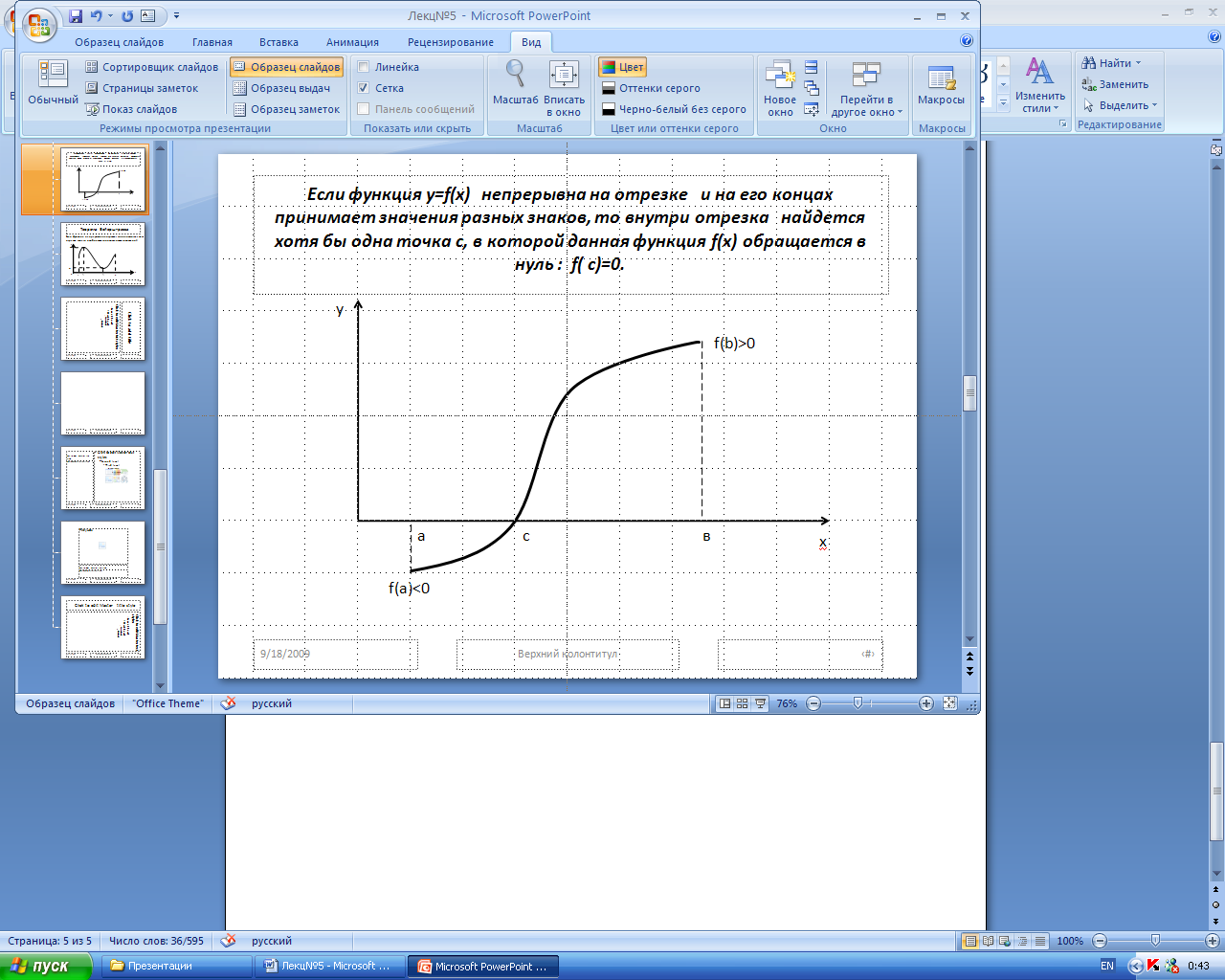
Данное утверждение лежит в основе метода «половинного деления», который используется для нахождения корня уравнения f(x)=0.

Метод половинного деления:

Для решения уравнения f(x)=0 с заданной точностью , необходимо :

1. Подобрать отрезок , такой, что на этом отрезке функция непрерывна и f(a) f(b)<0.

2. Вычислить

3. Если f(x)=0, то х- корень уравнения

4. Если 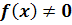, то если f(a)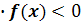 , то b=x , иначе a=x

5. Если , то х найден, иначе идти на пункт 2.

Лекция № 6

ПРОИЗВОДНАЯ ФУНКЦИИ

6.1. Понятие производной

Задача, приводящая к понятию производной:

Пусть материальная точка движется по закону . Пусть - путь, пройденный точкой к моменту времени . За время материальная точка прошла путь . Тогда средняя скорость точки за время равна . При получим мгновенную скорость точки в момент , т.е. .

Понятие производной

Пусть функция y=f(x) определена в некоторой окрестности точки . Дадим аргументу приращение , тогда функция получит приращение .

Отношение показывает среднюю скорость изменения функции относительно аргумента на промежутке .

Определение: Если существует конечный предел отношения приращения функции к приращению аргумента при , то этот предел называется производной функции в точке и обозначается

Для обозначения производной в точке применяются следующие обозначения:

Функция, имеющая производную в каждой точке интервала, называется дифференцируемой на этом интервале. Операция нахождения производной функции называется дифференцированием.

Определение: Закон, по которому каждой точке ставится в соответствие производная в этой точке, называется производной функции на множестве (a,b).

Для обозначения производной функции применяются следующие обозначения:

6.2. Связь между непрерывностью и дифференцируемостью

Теорема : Если функция дифференцируема в некоторой точке, то она непрерывна в ней.

Доказательство: Пусть функция y=f(x) дифференцируема в некоторой точке x. Следовательно, существует предел

Отсюда, по теореме о связи функции, её предела и бесконечно малой функции, имеем: где при т.е.

Переходя к пределу, при получаем А это и означает, что функция y=f(x) непрерывна в точке x, ч.т.д.

Обратная теорема неверна: непрерывная функция может не иметь производной. Примером такой функции является функция

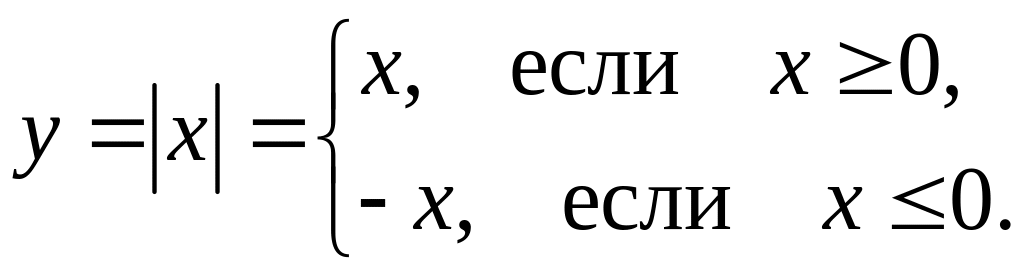
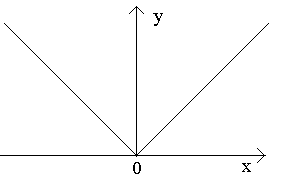
Изображённая на рисунке функция не прерывна в точке x=0, но не дифференцируема в ней.