Лекция № 3 Предел функции
3.1.Определение предела функции
Определение
1 ( «на языке 
»,
или по Коши):
Число А называется
пределом функции
при
,
если для любого числа
можно указать такое
,
что для любого х, удовлетворяющего
неравенству
,
выполняется неравенство
.
В этом случае пишут
.
Определение 2 ( «на языке последовательностей», или по Гейне ):
Число А называется
пределом функции f(x)
в точке a
(или при
),
если для любой последовательности
допустимых значений аргумента 
, сходящейся к a,
(т.е. 
),
последовательность соответствующих
значений функции сходится к числу А(т.е.
).
Заметим, что для существования предела функции в точке a вовсе не требуется, чтобы функция была непременно определена в точке a. Для того чтобы функция стремилась к пределу при , необходимо лишь, чтобы в области её определения были точки, как угодно близкие к a и отличные от a.
Пример:
Используя определение, доказать что
в точке
имеет предел, равный единице, т.е.
.
Решение. В данном
примере
,
А=1, и a=1. Возьмём любое
.
Задача состоит в том, чтобы по этому
найти такое
,
при котором из неравенства
следовало бы неравенство,
Преобразуя последнее неравенство,
получаем
,
или
Отсюда видно, что если взять
то
для всех x, удовлетворяющих неравенству
,
выполняется требуемое неравенство
.
Это означает, что
.
В частности, если
,
то
если
,
то
и т.д.
Заметим, что вычислить предел функции, используя только определение, довольно сложно. На практике обычно пользуются теоремами о пределах, которые приведены ниже.
Интервал
называется
–
окрестностью точки а.
Пользуясь этим названием, дадим
определение предел функции
при х стремящемся к а
(или в
точке в а):
Если для любого числа
существует
–
окрестность точки а,
такая, что для любого
из этой окрестности выполняется
неравенство
(
),
или значение функции попадает в 
-
окрестность точки А. (см. рис.)
Н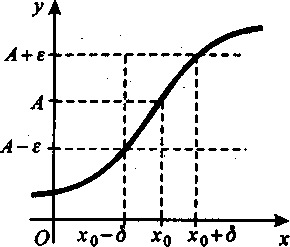
а
рис. видно, что при приближении точки x
к значению а,
значения
функции приближаются к числу А.
Естественно считать, что число А
– предел функции
при x,
стремящемся к а.
3.2. Односторонние пределы:
Если
число
есть
предел функции
при
х
стремящемся
к а
так,
что х
принимает
только значения, меньшие а,
то
называется
левым
пределом функции
в точке а:
Если
число
есть
предел функции
при
х
стремящемся
к а
так,
что х
принимает
только значения, большие а,
называется
правым
пределом функции
в точке а:
3.3. Бесконечно малые функции
Функция
называется
бесконечно
малой при
,
если
.
Определение.
Функция f(x)
называется бесконечно малой при
,
если 
.
3.4. Свойства бесконечно малых и бесконечно больших функций:
Произведение ограниченной при функции на б.м. при , есть функция б.м. при .
Произведение конечного числа б.м. при функции есть б.м. при функция.
Произведение постоянной на б.м. при функцию есть б.м. при функция.
Определение:
Функция
называется
бесконечно
большой при
,
если
т.е
,
или
Если функции и
-
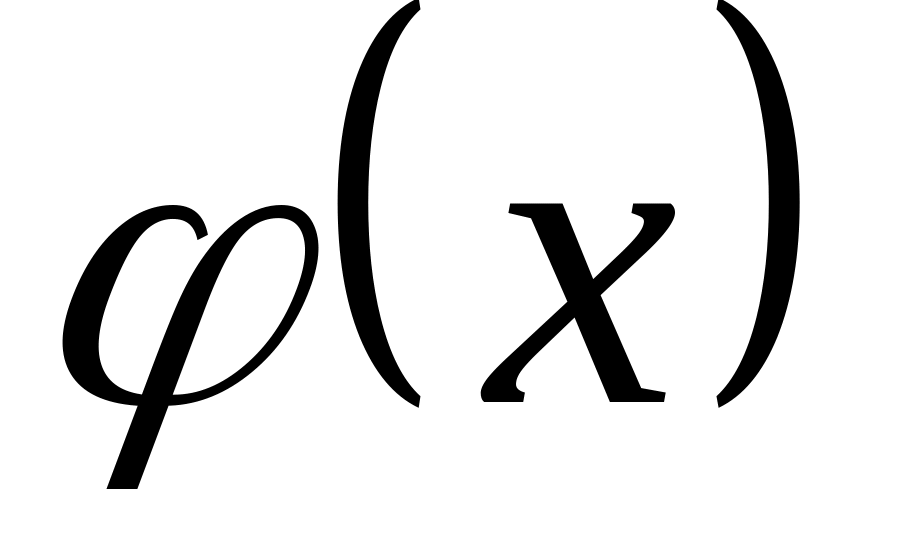бесконечно малые при
,
то их сумма
при
также
является бесконечно малой.Если функция – бесконечно малая при , а
-
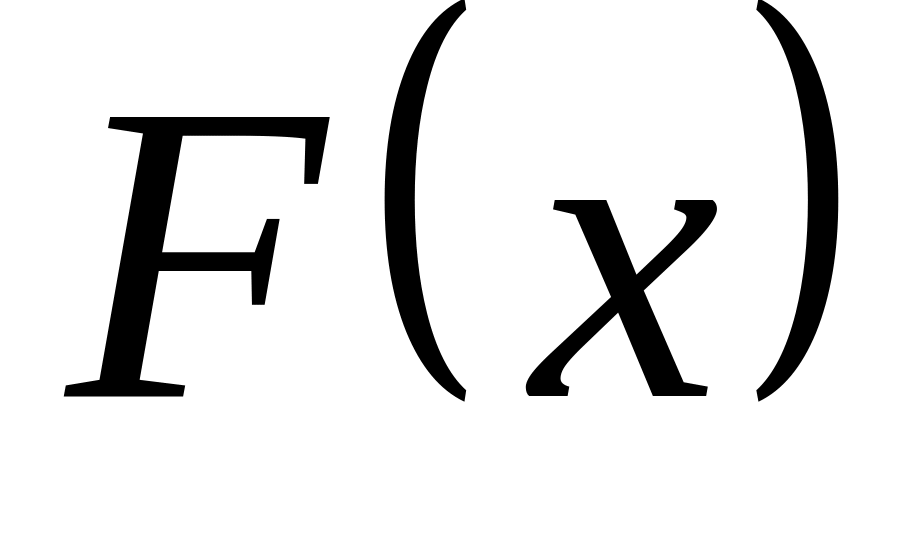ограниченная функция, то их произведение
есть функция бесконечно малая.Произведение конечного числа бесконечно малых функций есть величина бесконечно малая.
Если при функция имеет конечный предел
,а
функция
-
бесконечно большая, то
Если функция – бесконечно малая при , то функция
-
бесконечно большая, причем предполагается,
что в окрестности точки а функция f(x)
не обращается в нуль. Наоборот, если
при
функция 
-
бесконечно большая, то функция 
-
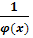бесконечно малая.
3.5. Теорема о единственности предела
Теорема:
Если
функция
имеет
предел при 
,
то этот предел единственный.
Доказательство:
Пусть
.
Допустим
.
Т.к.
,
то
:
(1)
Т.к.
,
то
:
(2)
Выберем
. Тогда при всех х, удовлетворяющих
условию:
выполняется (1) и (2).
Значит
,
т.е. разность
меньше любого наперед заданного
положительного
.
Значит
