
- •1.3. Функции, способы задания, свойства
- •1.Табличный, когда значения аргумента и соответствующие значения функции заданы таблицей.
- •2.Графический, когда соответствие аргумента и функции даны в виде графика;
- •3.Аналитический, когда зависимость дана в виде формулы.
- •1.4. Основные свойства функции:
- •1.5.Основные элементарные функции и их области определения
- •Функция определена на общей области определения функций f(X) и g(X), при условии, что g(X)≠0.
- •1.6. Сложная функция
- •1.7. Обратная функция
- •Пример: Графики двух взаимно- обратных функций -синий и - зеленый.
- •Лекция № 2 Последовательность. Предел числовой последовательности
- •2.1. Бесконечная числовая последовательность
- •2.2.Примеры
- •2. Написать общий член последовательности натуральных чисел, каждое из которых при делении на 3 дает остаток, равный 1.
- •3. Последовательность задана рекуррентным соотношением . Найти первые члены последовательности.
- •5. Доказать, что последовательность ограничена снизу и сверху.
- •2.3. Предел числовой последовательности
- •2.4. Теоремы о пределах
- •2.5. Предельный переход в неравенствах
- •2.6. Бесконечно малые и бесконечно большие последовательности
- •Лекция № 3 Предел функции
- •3.1.Определение предела функции
- •3.6. Связь между функцией, ее пределом и бесконечно малой функцией
- •3.10. Теорема о пределе монотонной функции
- •3.11. Некоторые обозначения
- •Примеры
- •Лекция № 4 Первый и второй замечательные пределы
- •4.1.Теорема (первый замечательный предел)
- •2) Пусть , тогда при .
- •4.2. Примеры
- •4.3. Второй замечательный предел. Число e.
- •4.4. Примеры
- •4.5. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции
- •4.6. Теоремы об эквивалентных бесконечно малых функциях
- •1) Функция f(X) определена в точке х0 и ее окрестности;
- •2) Функция f(X) имеет предел при х→х0 ;
- •3) Предел функции в точке х0 равен значению функции в этой точке.
- •5.2. Непрерывность функции в интервале и на отрезке
- •5.3. Точки разрыва и их классификация
- •2) Если , то х0 называется точкой конечного разрыва, а величину называют скачком функции.
- •5.4. Основные теоремы о непрерывных функциях
- •5.5. Свойства функций, непрерывных на отрезке
- •Вычислить
- •Если , то х найден, иначе идти на пункт 2.
- •6.2. Связь между непрерывностью и дифференцируемостью
- •6.3. Геометрический смысл производной
- •6.4. Основные правила дифференцирования
- •Правила дифференцирования:
- •6.5. Производная обратной функции
- •6.6. Производная неявно заданной функции
- •6.7. Производная показательно- степенной функции
- •6.8. Производная функции, заданной параметрически
- •Лекция № 7 Дифференциал функции
- •7.1. Понятие дифференциала
- •7.2.Геометрический смысл дифференциала
- •3. , Тогда
- •Лекция №8 Теоремы о дифференцируемых функциях
- •8.1. Теорема Ролля.
- •Найдём производную в точке
- •8.2. Теорема Коши
- •8.3. Теорема Лагранжа
- •8.4. Правило Лопиталя
- •Правило Лопиталя раскрытия неопределённостей вида
- •8.5. Правило Лопиталя для раскрытия неопределенности вида
- •Теорема остается справедливой и в том случае, если х ® ±¥ или х®х0±0;
- •Если опять дает неопределенность вида или , то правило Лопиталя следует применить еще раз.
- •Лекция № 9 Исследование функции и построение графика
- •9.1. Возрастание и убывание функции.
- •9.2. Интервалы монотонности функции
- •Теорема (необходимые условия монотонности):
- •Теорема (достаточные условия монотонности):
- •9.3. Экстремумы функции
- •Для исследования функции на экстремум, необходимо:
- •Исследовать знак производной f´(X) слева и справа от критических точек ( или исследовать знак второй производной в этих точках)
- •С помощью теорем о достаточном условии экстремума определить характер экстремума и вычислить его значение.
- •9. 4. Выпуклость графика функции. Точки перегиба.
- •9.5. Асимптоты графика функции.
- •9.6. Общая схема исследования функции и построения графика.
- •4. Найдем асимптоты графика функции.
- •5 . Для нахождения точек возможного экстремума найдем производную функции:
- •6. Для нахождения точек перегиба и интервалов выпуклости, вогнутости найдем вторую производную функции:
6.5. Производная обратной функции
Если
![]() дифференцируемая функция с отличной
от нуля производной, то производная
обратной функции
дифференцируемая функция с отличной
от нуля производной, то производная
обратной функции
![]() равна обратной величине производной
данной функции:
равна обратной величине производной
данной функции:
![]()
Доказательство:
![]() -
соответствующее приращение обратной
функции
.
-
соответствующее приращение обратной
функции
.
![]()
![]() (в силу
непрерывности обратной функции
при
(в силу
непрерывности обратной функции
при
![]() )
)
.
6.6. Производная неявно заданной функции
Если функция
задана неявно
![]() ,
следует продифференцировать обе части
тождества, применяя правило дифференцирования
сложной функции (помня, что
,
следует продифференцировать обе части
тождества, применяя правило дифференцирования
сложной функции (помня, что
![]() -
функция от
).
-
функция от
).
6.7. Производная показательно- степенной функции
Пусть
![]() ,
,
![]()
Прологарифмируем обе части:
![]()
![]()
![]()
![]()
![]()
![]() .
.
6.8. Производная функции, заданной параметрически
Часто применяется способ задания функции, при котором текущие координаты являются функцией третьей переменной величины, параметра t:
![]() ,
такой способ задания называется
параметрическим.
,
такой способ задания называется
параметрическим.
![]() перейдем
к пределу:
перейдем
к пределу:
 Получаем:
Получаем:
![]() .
.
Пример:
![]() Найти у/.
Найти у/.
x/t
= 2а
sint×cost;
y/t
= -3а
cos2t×sint,
тогда у/
=
![]() = -1,5cost.
= -1,5cost.
Лекция № 7 Дифференциал функции
7.1. Понятие дифференциала
Пусть функция
имеет в точке х
отличную
от нуля производную ![]() .
Тогда по теореме о связи функции, ее
предела и бесконечно малой функции,
приращение функции можно записать:
.
Тогда по теореме о связи функции, ее
предела и бесконечно малой функции,
приращение функции можно записать:
![]()
![]()
Где
-
постоянная, не зависящая от
,
![]() - б.м. более высокого порядка малости,
чем
- б.м. более высокого порядка малости,
чем
![]() .
Дифференциалом функции y=f(x)
в точке
называется главная часть приращения
функции, линейная относительно
,
.
Дифференциалом функции y=f(x)
в точке
называется главная часть приращения
функции, линейная относительно
,
Обозначается:
![]() , или
, или
![]()
![]()
Дифференциал dy называется также дифференциалом первого порядка .
Найдем дифференциал
независимой переменной х, т.е. дифференциал
функции y=x.
Так как ![]() , то
, то ![]() , т.е. дифференциал независимой
переменной равен приращению этой
переменной. Поэтому
, т.е. дифференциал независимой
переменной равен приращению этой
переменной. Поэтому
![]()
дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной .
Теорема Если функция имеет дифференциал в точке , то функция имеет производную в этой точке и обратно.
Доказательство:
Пусть функция y=f(x) дифференцируема в точке х, т.е.
 разделив это равенство на
разделив это равенство на  и взяв предел при
и взяв предел при 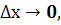 получим:
получим:
![]() т.е. функция имеет
производную в точке х.
т.е. функция имеет
производную в точке х.
Обратно:
2)Пусть функция
y=f(x)
имеет производную в точке х, т.е.
![]() ,
,
![]() -
б.м. при
-
б.м. при
![]() ,
где
,
где
![]() -
б.м. более высокого порядка, т.е. функция
имеет дифференциал в точке х.
-
б.м. более высокого порядка, т.е. функция
имеет дифференциал в точке х.
7.2.Геометрический смысл дифференциала
 Выясним
геометрический смысл дифференциала.
Выясним
геометрический смысл дифференциала.
Для этого проведём
к графику функции y=f(x) в точке M(x;y)
касательную MT и рассмотрим ординату
этой касательной для точки
![]() (см. рис.). На рисунке
(см. рис.). На рисунке
![]() Из
прямоугольного треугольника MAB имеем:
Из
прямоугольного треугольника MAB имеем:
 т.е.
т.е.
![]()
Но, согласно
геометрическому смыслу производной,
![]() Поэтому
Поэтому
![]()
Сравнивая
полученный результат с формулой
![]() получаем
получаем
![]() т. е. дифференциал функции y=f(x) в точке
x равен приращению ординаты касательной
графику функции в этой точке, когда x
получит приращение
т. е. дифференциал функции y=f(x) в точке
x равен приращению ординаты касательной
графику функции в этой точке, когда x
получит приращение
![]() .
.
7.3. Приложение дифференциала к приближенным вычислениям
Т.к.
![]() ,
где
,
где
![]() -
б.м.
-
б.м.
То
![]()
![]()
Используя это равенство можно оценивать приближенное значение функции вблизи точек, в которых известно точное значение функций.
7.4.Свойства дифференциала функции
Производная как
отношение дифференциалов. Пусть
![]() ,
тогда
,
тогда
![]() , тогда
, тогда
![]() , т.е. производная равна отношению
дифференциалов.
, т.е. производная равна отношению
дифференциалов.
1.
![]()
2.
![]()
