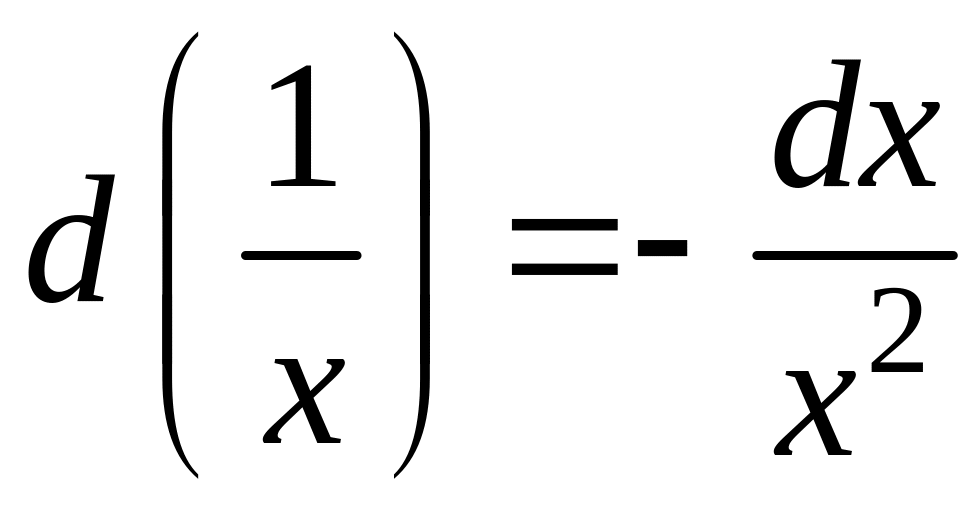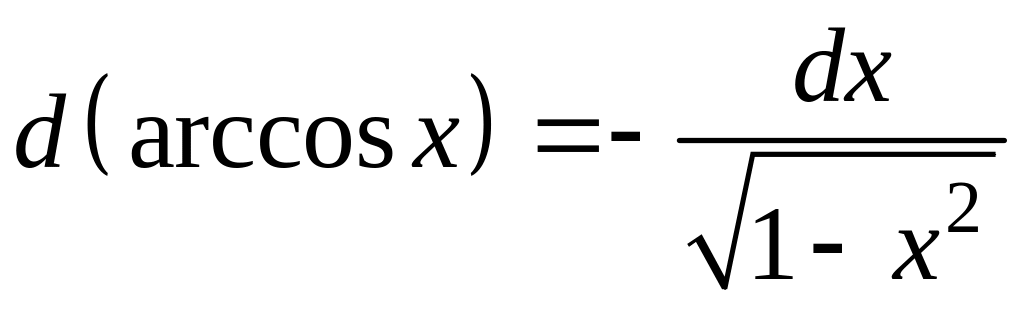- •1.3. Функции, способы задания, свойства
- •1.Табличный, когда значения аргумента и соответствующие значения функции заданы таблицей.
- •2.Графический, когда соответствие аргумента и функции даны в виде графика;
- •3.Аналитический, когда зависимость дана в виде формулы.
- •1.4. Основные свойства функции:
- •1.5.Основные элементарные функции и их области определения
- •Функция определена на общей области определения функций f(X) и g(X), при условии, что g(X)≠0.
- •1.6. Сложная функция
- •1.7. Обратная функция
- •Пример: Графики двух взаимно- обратных функций -синий и - зеленый.
- •Лекция № 2 Последовательность. Предел числовой последовательности
- •2.1. Бесконечная числовая последовательность
- •2.2.Примеры
- •2. Написать общий член последовательности натуральных чисел, каждое из которых при делении на 3 дает остаток, равный 1.
- •3. Последовательность задана рекуррентным соотношением . Найти первые члены последовательности.
- •5. Доказать, что последовательность ограничена снизу и сверху.
- •2.3. Предел числовой последовательности
- •2.4. Теоремы о пределах
- •2.5. Предельный переход в неравенствах
- •2.6. Бесконечно малые и бесконечно большие последовательности
- •Лекция № 3 Предел функции
- •3.1.Определение предела функции
- •3.6. Связь между функцией, ее пределом и бесконечно малой функцией
- •3.10. Теорема о пределе монотонной функции
- •3.11. Некоторые обозначения
- •Примеры
- •Лекция № 4 Первый и второй замечательные пределы
- •4.1.Теорема (первый замечательный предел)
- •2) Пусть , тогда при .
- •4.2. Примеры
- •4.3. Второй замечательный предел. Число e.
- •4.4. Примеры
- •4.5. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции
- •4.6. Теоремы об эквивалентных бесконечно малых функциях
- •1) Функция f(X) определена в точке х0 и ее окрестности;
- •2) Функция f(X) имеет предел при х→х0 ;
- •3) Предел функции в точке х0 равен значению функции в этой точке.
- •5.2. Непрерывность функции в интервале и на отрезке
- •5.3. Точки разрыва и их классификация
- •2) Если , то х0 называется точкой конечного разрыва, а величину называют скачком функции.
- •5.4. Основные теоремы о непрерывных функциях
- •5.5. Свойства функций, непрерывных на отрезке
- •Вычислить
- •Если , то х найден, иначе идти на пункт 2.
- •6.2. Связь между непрерывностью и дифференцируемостью
- •6.3. Геометрический смысл производной
- •6.4. Основные правила дифференцирования
- •Правила дифференцирования:
- •6.5. Производная обратной функции
- •6.6. Производная неявно заданной функции
- •6.7. Производная показательно- степенной функции
- •6.8. Производная функции, заданной параметрически
- •Лекция № 7 Дифференциал функции
- •7.1. Понятие дифференциала
- •7.2.Геометрический смысл дифференциала
- •3. , Тогда
- •Лекция №8 Теоремы о дифференцируемых функциях
- •8.1. Теорема Ролля.
- •Найдём производную в точке
- •8.2. Теорема Коши
- •8.3. Теорема Лагранжа
- •8.4. Правило Лопиталя
- •Правило Лопиталя раскрытия неопределённостей вида
- •8.5. Правило Лопиталя для раскрытия неопределенности вида
- •Теорема остается справедливой и в том случае, если х ® ±¥ или х®х0±0;
- •Если опять дает неопределенность вида или , то правило Лопиталя следует применить еще раз.
- •Лекция № 9 Исследование функции и построение графика
- •9.1. Возрастание и убывание функции.
- •9.2. Интервалы монотонности функции
- •Теорема (необходимые условия монотонности):
- •Теорема (достаточные условия монотонности):
- •9.3. Экстремумы функции
- •Для исследования функции на экстремум, необходимо:
- •Исследовать знак производной f´(X) слева и справа от критических точек ( или исследовать знак второй производной в этих точках)
- •С помощью теорем о достаточном условии экстремума определить характер экстремума и вычислить его значение.
- •9. 4. Выпуклость графика функции. Точки перегиба.
- •9.5. Асимптоты графика функции.
- •9.6. Общая схема исследования функции и построения графика.
- •4. Найдем асимптоты графика функции.
- •5 . Для нахождения точек возможного экстремума найдем производную функции:
- •6. Для нахождения точек перегиба и интервалов выпуклости, вогнутости найдем вторую производную функции:
3. , Тогда
4.
![]() ,
,
![]()
5.
![]()
7.5.Дифференциал сложной функции
Теорема: Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента (если обе функции дифференцируемы)
Доказательство:
,
пусть
![]() ,
,
![]()
По правилу диф. сложной функции:
![]() .
Умножим на
.
Умножим на
![]() обе части:
обе части:
![]()
![]() Замечание: здесь
-
функция, а
-
независимая переменная. Отсюда следует
свойство инвариантности
дифференциала:
Дифференциал равен произведению
производной функции на дифференциал
аргумента, при этом безразлично, является
ли аргумент независимой переменной или
функцией.
Замечание: здесь
-
функция, а
-
независимая переменная. Отсюда следует
свойство инвариантности
дифференциала:
Дифференциал равен произведению
производной функции на дифференциал
аргумента, при этом безразлично, является
ли аргумент независимой переменной или
функцией.
Таблица дифференциалов
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производные и дифференциалы высших порядков
Определение.
Второй производной, или производной
второго порядка, называется производная
от первой производной. Обозначается
![]() .
Для обозначения второй производной
используются символы:
.
Для обозначения второй производной
используются символы:
![]()
Определение. Дифференциалом второго порядка называется дифференциал от первого дифференциала.
![]() ,
т.к.
,
т.к.
![]() ,
то
,
то
![]() -
постоянная по отношению к
.
-
постоянная по отношению к
.
![]() ,
т.е.
,
т.е.
![]()
Замечание: Дифференциалы высших порядков свойством инвариантности не обладают.
Лекция №8 Теоремы о дифференцируемых функциях
Рассмотрим ряд теорем, имеющих большое теоретическое и прикладное значение
8.1. Теорема Ролля.
Если функция f(x)
непрерывна на отрезке
![]() ,
дифференцируема на интервале
,
дифференцируема на интервале
![]() и на концах отрезка принимает одинаковые
значения f(a)=
f(b),
то найдётся, хотя бы одна точка
и на концах отрезка принимает одинаковые
значения f(a)=
f(b),
то найдётся, хотя бы одна точка
![]() ,
в которой производная
,
в которой производная
![]() обращается в нуль, т.е.
обращается в нуль, т.е.
![]()
Доказательство. Так как функция f(x) непрерывна на отрезке , то она достигает на этом отрезке своего наибольшего и наименьшего значений, соответственно, M и m.
Если m=M,
то функция f(x)
постоянна на
и, следовательно, её производная
![]() в любой точке отрезка
.
в любой точке отрезка
.
Если
![]() ,
то функция достигает, хотя бы одно из
значений M или
m во внутренней
точке с интервала
,
т. к. f(a)=
f(b).
,
то функция достигает, хотя бы одно из
значений M или
m во внутренней
точке с интервала
,
т. к. f(a)=
f(b).
Пусть, например, функция принимает
значение M в
точке
![]() ,
т. е. f(c)=M.
Тогда для всех
,
т. е. f(c)=M.
Тогда для всех
![]() выполняется соотношение
выполняется соотношение
![]()
Найдём производную в точке
![]()
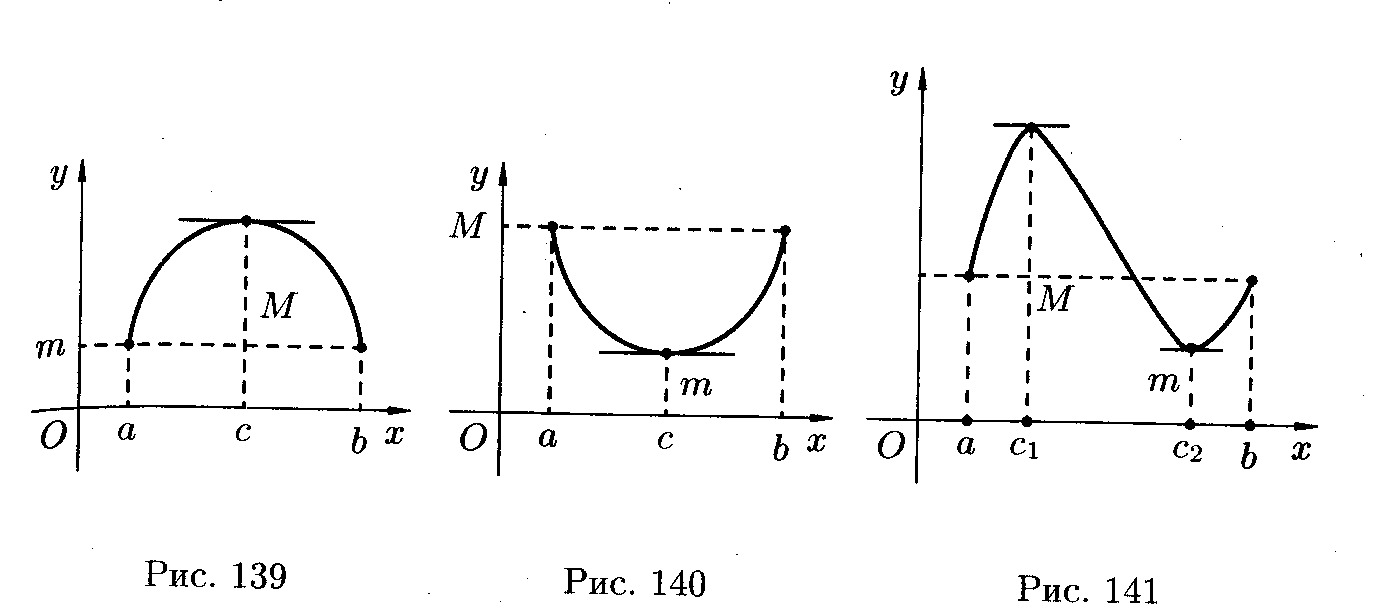
Рис. 1
Рис. 2
Рис. 3
В силу условия
верно неравенство
![]() .
Если
.
Если
![]() (т. е.
(т. е.
![]() справа
от точки x=c),
то
справа
от точки x=c),
то
![]() и
поэтому
и
поэтому
![]()
Если,
![]() то
то
![]() и
и
![]()
Таким образом,
В случае, когда f(c)=m, доказательство аналогичное. Ч.т.д.
Геометрически теорема Ролля означает, что на графике функции y=f(x) найдётся точка, в которой касательная к графику параллельна оси Ox (см. рис.1 и 2). На рис. 3 таких точек две.
8.2. Теорема Коши
Если функции f(x)
и (x)
непрерывны на отрезке
,
дифференцируемы на интервале
,
причём
![]() для
,
то найдётся хотя бы одна точка
такая, что выполняется равенство
для
,
то найдётся хотя бы одна точка
такая, что выполняется равенство
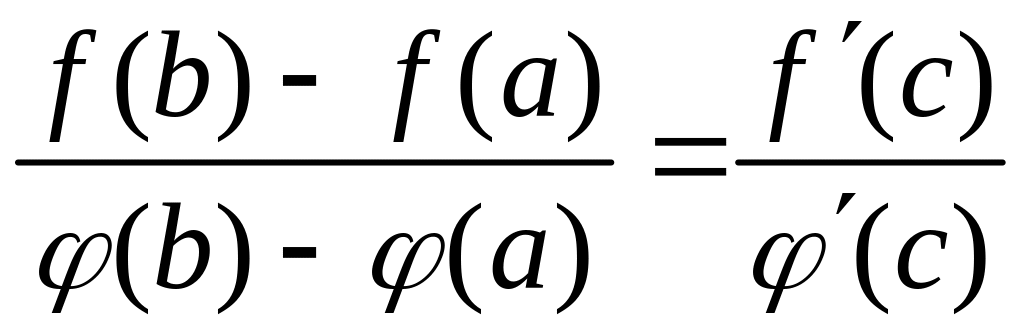 .
.
Доказательство. Отметим, что
![]() ,
т. к. в противном случае по теореме Ролля
нашлась бы точка c,
такая, что
,
т. к. в противном случае по теореме Ролля
нашлась бы точка c,
такая, что
![]() ,
чего не может быть по условию теоремы.
Рассмотрим вспомогательную функцию
,
чего не может быть по условию теоремы.
Рассмотрим вспомогательную функцию
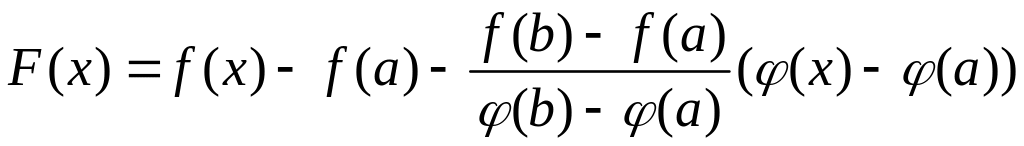 .
.
Она удовлетворяет всем условиям
теоремы Ролля: непрерывна на отрезке
и дифференцируема на интервале
,
т. к. является линейной комбинацией
функций f(x)
и (x);
на концах отрезка она принимает одинаковые
значения
![]() .
.
На основании теоремы Ролля найдётся
точка
такая, что
![]() .
Но
.
Но
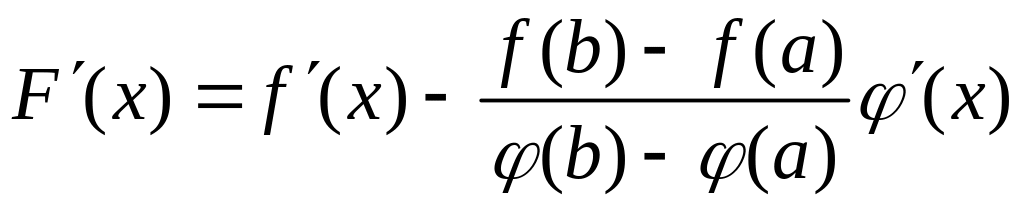 ,
следовательно,
,
следовательно,
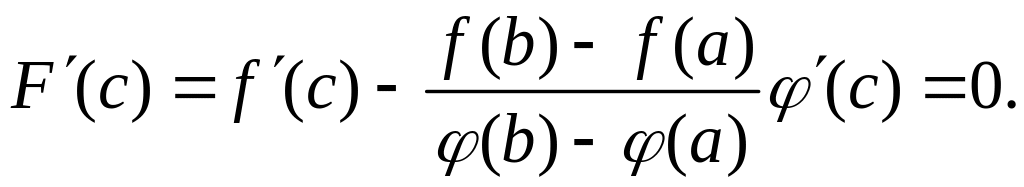
Отсюда следует
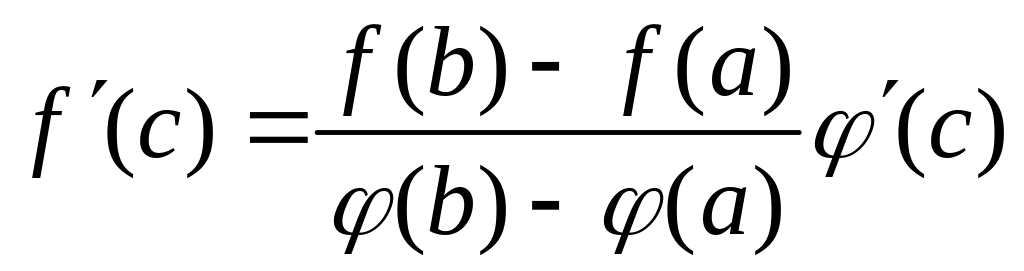 и
и
 Ч.т.д.
Ч.т.д.