Для исследования функции на экстремум, необходимо:

1. Найти критические точки функции y=f(x)

2. Исследовать знак производной f´(X) слева и справа от критических точек ( или исследовать знак второй производной в этих точках)

3. С помощью теорем о достаточном условии экстремума определить характер экстремума и вычислить его значение.

9. 4. Выпуклость графика функции. Точки перегиба.

О пределение: График функции называется выпуклым вниз (вогнутым) на интервале (a;b), если он расположен выше любой ее касательной на этом интервале; выпуклым вверх (выпуклым) на интервале (a;b), если он расположен ниже любой ее касательной на этом интервале.

Точка, где меняется направление выпуклости, называется точкой перегиба.

Теорема:

Если функция y = f(x) во всех точках интервала имеет отрицательную производную, т. е. , то график функции в этом интервале выпуклый вверх. Если же - график выпуклый вниз.

Доказательство. Пусть . Возьмём на графике функции произвольную точку M с абсциссой и проведём через M касательную .

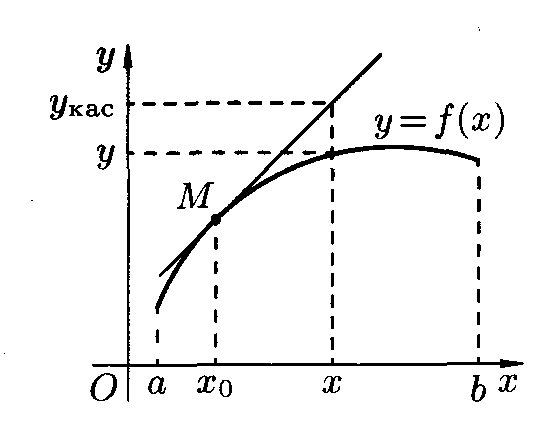
Покажем, что график функции расположен ниже этой касательной. Для этого сравним в точке y кривой y = f(x) с ординатой yкас её касательной. Уравнение касательной, как известно, есть , т.е. . Тогда . По теореме Лагранжа, , где с лежит между x0 и x. Поэтому , т. е. .

Разность снова преобразуем по формуле Лагранжа:

, где с1 лежит между x0 и с. Таким образом, получаем .

Исследуем это равенство:

если , то и . Следовательно, , т. е. :

е сли , то и . Следовательно, , т. е. :

Итак, доказано, что во всех точках интервала ордината касательной больше ординаты графика, т. е. график функций выпуклый вверх. Аналогично доказывается, что при график выпуклый вниз. Ч. т. д.

Теорема 9.6. (достаточное условие существования точек перегиба). Если вторая производная f′′(x) при переходе через точку х₀ , в которой она равна нулю или не существует, меняет знак, то эта точка есть точка перегиба.

9.5. Асимптоты графика функции.

Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой.

Асимптоты могут быть вертикальными, наклонными и горизонтальными.

1. Прямая х=а является вертикальной асимптотой графика функции

y=f(x), если .

2. Уравнение наклонной асимптоты y=kx+b,

где , конечные пределы.

Если хотя бы один из пределов не существует или равен бесконечности, то кривая y=f(x) наклонной асимптоты не имеет.

Если k=0, то кривая имеет горизонтальную асимптоту y=b.

у

Н

0

апример, на рисунке кривая

имеет вертикальную асимптоту х = - 1.

x

-1