2.4.3 Определение неизвестной случайной величины

В процессе эксплуатации продукции или специальных испытаний на надежность возникает необходимость экспериментально оценить неизвестные параметры, как например, среднее время безотказной работы Т_о; среднее время восстановления Т_в; интенсивность отказов и т. п.

Методика и последовательность решения задачи статистической оценки различных неизвестных параметров имеет определенную общность. Рассмотрим решение задачи экспериментальной оценки неизвестного параметра безотказности Т_о некоторой радиолокационной системы, испытываемой в процессе эксплуатации.

Так как величина Т_о является математическим ожиданием случайной величины Т — времени безотказной работы между отказами, т. е.

то, естественно, для оценки параметра Т_о необходимо в качестве исходных статистических данных располагать фактическими частными реализациями случайной величины Т, т. е. иметь набор опытных данных: ^.

В каждой из случайных величин содержится определенная информация о законе распределения случайной величины Т и о ее математическом ожидании Т_о. В отличие от оценки неизвестного закона F(t), когда требовался большой объем статистических данных (n >100), число п реализаций T =t_i при оценке Т_о может быть любым, в том числе и малым. Однако при малой статистике точность и достоверность оценки могут оказаться недостаточными, поэтому обычно требуют, чтобы число реализаций п при оценке параметра Т_о было бы больше десяти, хотя и при меньших п можно указать соответствующие точность и достоверность оценки.

В процессе статистической оценки определяется не сама неизвестная величина Т_о, а ее опытное значение или точечная оценка , причем .

Это приближенное вероятностное равенство тем точнее и достовернее, чем больший объем исходной статистики используется для расчета экспериментальной величины. Так как для расчета опытной величины используются частные реализации случайной величины , то и сама является случайной величиной. Этим объясняется характер приближенного равенства .

Задачу оценки неизвестного параметра Т_о сформулируем следующим образом.

Дан некоторый набор п исходных статистических данных , при i=l, 2, 3,..., п.

Требуется оценить неизвестный параметр безотказности T₀

Решение. Для правильной и полной статистической оценки неизвестного параметра Т_о по результатам эксперимента необходимо:

А. определить, по какой формуле рассчитывать наилучшую статистическую оценку для неизвестного параметра T₀ , используя исходную статистику;

Б. определить какова достоверность и точность получаемой оценки.

А. Наилучшая статистическая оценка

Используя исходные статистические данные, можно предложить несколько формул для расчета опытного случайного значения , например:

28

Но какая же из всех возможных формул дает наилучшую оценку для Т₀?

В методах математической статистики под наилучшей статистической оценкой для неизвестного параметра Т_о выбирается такая формула-оценка , которая удовлетворяет трем основным требованиям: состоятельности; несмещенности; эффективности.

Так как статистическая оценка является случайной величиной, то она имеет свой закон распределения, математическое ожидание и дисперсию.

Свойство состоятельности оценки заключается в том, что при п ее математическое ожидание М() сходится к математическому ожиданию Т₀ = М (Т) изучаемой случайной величины Т:

Если при любых значениях n (в том числе и при малых), то такая оценка обладает свойством несмещенности.

Та оценка, которая имеет наименьшую дисперсию, является эффективной оценкой.

Формула для расчета наилучшей статистической оценки зависит от вида плотности вероятности F(t) случайных величин , входящих в эту формулу.

Используя известный в математической статистике метод максимума правдоподобия, можно показать, что если плотность вероятности F(t) исходных случайных величин имеет экспоненциальное распределение, т. е.

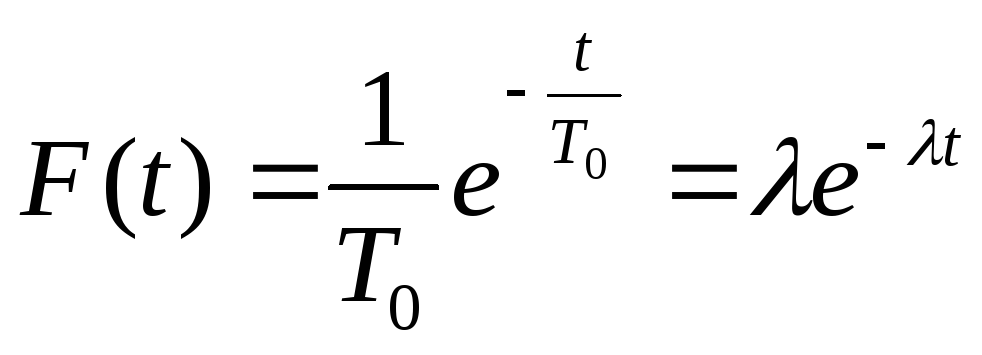29

то наилучшая статистическая оценка для неизвестного параметра Т₀ должна рассчитываться по формуле

30

Например, если имеется t₁ = 72 ч, t₂ = 56 ч, t₃= 103 ч, то наилучшая оценка равна:

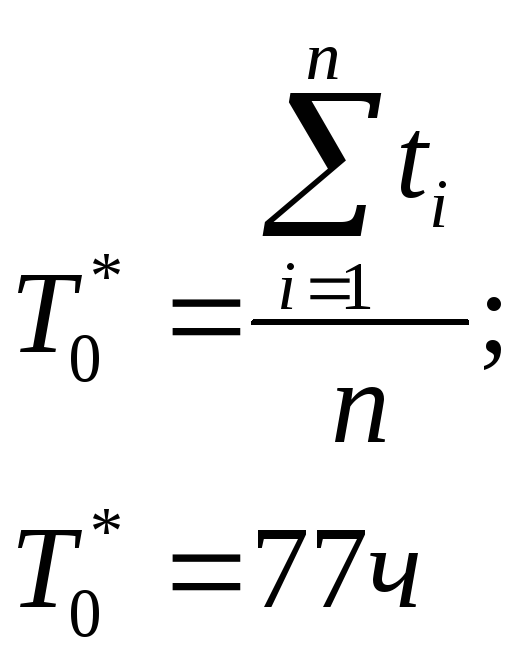
Значит ли это, что неизвестный параметр Т_о тоже равен 77 часам ? Конечно, нет! Т_о = 77 ч только по вероятности. Если повторить эксперимент по оценке Т_о в тех же условиях и снова набрать три значения , то в общем случае получим новое число

Но по прежнему будет справедливо вероятностное приближение Т_о. Значит, случайное число в каждом повторении опыта при п = const будет принимать случайные значения , приблизительно равные значению неизвестного числа Т_о.

Д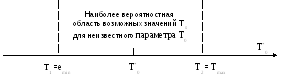 остоверность определяет степень уверенности в том, что данное статистическое утверждение истинно.

Рис. 18 Иллюстрация нахождения случайных значений

Следовательно, если по результатам эксперимента получена какая-то оценка , рассчитанная по формуле (30), то можно лишь с некоторой вероятностной уверенностью утверждать, что область наиболее возможных значений для Т_о находится где-то в районе случайного числа (см. рис.18). Есть лишь некоторая достоверность того, что неизвестное число Т_о лежит где-то между левой минимальной границей и правой максимальной Т₂= Т_шах.

Следовательно, для того чтобы статистически полно определить приближенное вероятностное равенство, необходимо указать достоверность и точность оценки. Количественно достоверность измеряется вероятностью того, что возможные значения неизвестного параметра заключены в определенном интервале. Этот интервал называется доверительным интервалом, а его границы — доверительными границами.

Достоверность численно равна вероятности того, что оцениваемый параметр заключен в доверительном интервале.

Точность оценки определяется численными значениями границ доверительного интервала (т. е. его левого, минимального, и правого, максимального, значения).

Если достоверность велика, то велика и практическая уверенность в том, что неизвестный параметр, действительно, заключен между указанными доверительными границами. Поэтому доверительная вероятность физически обозначает меру практической уверенности в истинности статистической оценки.

Применительно к изучаемому вопросу оценки неизвестного параметра Т₀ доверительная вероятность равна:

31

Величина доверительного интервала () (см. рис.18) характеризует точность статистической оценки неизвестного параметра безотказности Т_о. Таким образом, характеризуя точность оценки Т_о, можно указать, что возможные значения для Т₀ заключены в пределах между Т₁ и Т₂, т. е.

.

Другими словами можно сказать, что достоверность — это практическая гарантия того, что Т_о находится в заданных пределах точности оценки.

Следовательно, если зафиксировать границы точности оценки, то с ростом n увеличивается достоверность оценки. В практических расчетах доверительная вероятность принимается в интервале 90- 99 %. Доверительные границы выбираются таким образом, чтобы вероятность 1 - делилась поровну слева от минимального значения и справа от максимального значения. Так, при принятой доверительной вероятности = 90%, нижняя граница определится вероятностью от 5% до нуля, а верхняя граница от 95% до 100%. Левые и правые значения численно равны площадям под кривой распределения и позволяют определить коэффициенты точности оценки и . Отсюда подставляя вместо неизвестного параметра его наилучшую оценку, получим:

, представляющую нижнюю границу и , представляющую верхнюю границу. Значения коэффициентов точности табулированы и выбираются при задании объема выборки и заданной доверительной вероятности (беря значения верхней границы - ½(1-) и нижней границы 1 -½(1-)).

Рассмотрим пример для трех значений времени ,

1. ,

2. Из таблицы определяем значение коэффициента для нижней границы и для верхней границы .

3. С доверительной вероятностью 90% утверждаем, что неизвестный параметр Т₀ заключен в пределах:

.

Следует напомнить, что увеличение доверительной вероятности приведет к расширению интервала!