21 Билет. Теоремы об арифметических свойствах пределов последовательности:

теорема1. Если последовательности {x_n} и {y_n} сходятся,то сходиться последовательность {x_n+y_n} и справедлива формула:

краткая формульровка этой теоремы: преде суммы равен сумме пределов, если пределы {x_n} _и {y_n} существуют и конечны.

Теорема2. Предел производной равен произведению пределов:

, если пределы {x_n} и {Y_n} существуют и конечны.

Теорема3. Постоянную велечину можно выносить за знак предела:

Lim(с* a_n)= c* lim a_n

Теорема4. Предел отношения равен обношению пределов:

. если пределы {X_n} и {Y_n} существуют и конечны.( )

доказательство:

докажем теорему1: пусть , а lim y_n=y

(n стремиться к бесконечн). Возьмем произвольное число E(эпсюл)>о. Тогда существуют числа N₁ и N₂ такие, что при всех n>N₁ |x_n-x|> E/2,

при всех n>N_{2 |}y_n-y|<E/2.

Пусть N₃- число больше,чем N₁ и N₂.Тогда при n>N₃ последние два неравенства истинны одновременно. Поэтому: |(x_n+y_n)-(x+y)|=|(x_n-x)+(y_n-y)|</=|x_n-x|+|y_n-y|<E/2+E/2=E

Следовательно последовательность x_n+y_n сходиться и

Остальные правила доказываются аналогично.

22.Признаки существования предела последовательности.

Теорема 1 (теорема о двух милиционерах). Если функция y=f(x) в некоторой окрестности точки а заключена между двумя функциями и , т.е. выполняется неравенство х, причем эти функции имеют одинаковый предел при, то существует предел функции y=f(x) при, равный этому же значению.

,

=> .

Теорема 2. Если функция y=f(x) монотонно возрастет (убывает) в некоторой окрестности точки а и ограничена сверху (снизу), то она имеет предел при.

Признаки существования предела

1. Если

2. Монотонная и ограниченная последовательность имеет предел.

3. Числовая последовательность (x_n) имеет конечный предел тогда и только тогда когда

(критерий Коши).

23. Замечательный предел типа «е».

Последовательность , имеет конечный предел, называемый числом е:

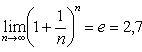
24. Предел функции в точке.

Если функция f (x) имеет предел в точке a, то этот предел единственный.

Число A₁ называется пределом функции f (x) слева в точке a, если для каждого ε > 0 существует δ > 0 такое, что для всех выполняется неравенство  

Число A₂ называется пределом функции f (x) справа в точке a, если для каждого ε > 0 существует δ > 0 такое, что для всех выполняется неравенство  

Предел слева обозначается предел справа – Эти пределы характеризуют поведение функции слева и справа от точки a. Их часто называют односторонними пределами. В обозначении односторонних пределов при x → 0 обычно опускают первый нуль: и .

Если функции f (x) и g (x) имеют конечные пределы в точке a, причем   то

, ,

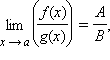
если B ≠ 0 и если g (x) ≠ 0 в δ-окрестности точки a.

25. Определение предела функции на языке языке «ε» — «δ».

НЕТ 26-30

31. Теоремы об арифметических свойствах пределов.

Теорема 1. (о единственности предела функции). Функция не может иметь более одного предела.

Следствие. Если две функции f(x) и g(x) равны в некоторой окрестности точки , за исключением, может быть, самой точки , то либо они имеют один и тот же предел при , либо обе не имеют предела в этой точке.

Теорема 2. Если функции f(x) и  g(x) имеют пределы в точке , то:

1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.

         (2)

2) предел произведения функций равен произведению пределов сомножителей, т.е.

            (3)

3)предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.

           (4)

Замечание. Формулы (2) и (3) справедливы для любого конечного числа функций.

Следствие 1. Предел постоянной равен самой постоянной, т.е.

Следствие 2. Постоянный множитель можно выносить за знак предела, т.е.

Теорема 3 (о пределе сложной функции). Если существует конечный предел

а функция f(u) непрерывна в точке , то

Другими словами, для непрерывных функций символы предела и функции можно поменять местами.