69. Определение несобственных интегралов с бесконечными пределами.

Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий: Предел a или b (или оба предела) являются бесконечными; Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b]. Иногда такой несобственный интеграл еще называют несобственным интегралом первого рода. Несобственный интеграл может быть отрицательным. Несобственный интеграл выражает площадь бесконечно длинной криволинейной трапеции.

Если интеграл, определенный от а до b при b —> +oo имеет конечный предел, то этот предел называется несобственным интегралом функции f(x) от а до бесконечности .

Если интеграл при b —> +00 имеет бесконечный предел или вовсе не имеет предела, то говорят, что несобственный интеграл расходится. Если интеграл при b —> +00 имеет конечный предел, то говорят, что несобственный интеграл сходится.

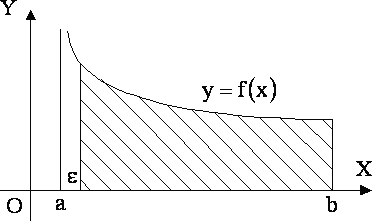
70. Несобственные интегралы от разрывных функций.

Рассмотрим случай, когда функция непрерывна на промежутке , а в точке терпит разрыв второго рода. В этом случае введение определенного интеграла на отрезке как предела интегральной суммы также невозможно. Необходимо искать площадь трапеции, левый конец основания которой приближается к точке .

Определение. Если существует конечный предел , то этот предел называется несобственным интегралом от разрывной функции и обозначается .

Следовательно, вычисление несобственного интеграла от разрывной функции связано с нахождением предела:

Так же как и в предыдущем параграфе, если этот предел существует, то интеграл называется сходящимся, если не существует или равен бесконечности, то – расходящимся.

С геометрической точки зрения несобственный интеграл от разрывной функции равен площади криволинейной трапеции, у которой в какой-то точке высота равна бесконечности.

71. Интеграл вероятностей (Пуассона).

Интеграл Пуассона – это интеграл вида

,

где r и j — полярные координаты, q — параметр, меняющийся на отрезке [0; 2p]; Интеграл Пуассона выражает значения функции u (r, j), гармонической внутри круга радиуса R, через её значения f(q), заданные на границе этого круга. Функция u (r, j) является решением задачи Дирихле для круга. Интеграл Пуассона был впервые рассмотрен  Пуассоном (1823). Строгая теория этого интеграла была создана Г. Шварцем (1869).

  2) Интеграл

;

встречается в теории вероятностей и некоторых задачах математической физики. Пуассон предложил весьма простой приём для вычисления этого интеграла. Впервые же этот интеграл был вычислен (1729) Л. Эйлером, поэтому называется также интегралом Эйлера — Пуассона.