
- •1 Билет. Понятие множества , элемента множества.
- •2 Билет. Конечные и бесконечные множества.
- •3 Билет. Свойства операций объединения и пересечения множеств.
- •4 Билет. Прямое произведение множеств.
- •5 Билет. Бинарные отношения.
- •6. Функция как закон соответствия между множествами
- •7. Класс элементарных функций
- •8. Суперпозиция функций.
- •9. Последовательность - функция натурального аргумента.
- •10. Бесконечно малые последовательности
- •11 Билет. «»
- •12 Билет. «»
- •21 Билет. Теоремы об арифметических свойствах пределов последовательности:
- •22.Признаки существования предела последовательности.
- •23. Замечательный предел типа «е».
- •24. Предел функции в точке.
- •25. Определение предела функции на языке языке «ε» — «δ».
- •31. Теоремы об арифметических свойствах пределов.
- •32. Сравнение бесконечно малых функций
- •33.«Замечательный» предел - предел отношения синуса бесконечно малого угла к этому углу.
- •34. Определение непрерывности функции в точке.
- •41 Определение производной.
- •42 Приращение функции и вычисление средней скорости изменения функции.
- •43 Геометрический смысл производной.
- •44 Связь между непрерывностью и существованием производной.
- •45) Правила вычисления производной от суммы, произведения и частного функций.
- •46 Производная сложной функции
- •48 Бином Ньютона. Формула Ньютона-Лейбница.
- •49 Теорема Лагранжа о конечном приращении функции на отрезке.
- •50 Правило Лопиталя раскрытия неопределенностей.
- •51.Понятие о дифференциале функции.
- •52.Геометрический смысл дифференциала функции.
- •53.Связь дифференциала и производной функции.
- •54.Свойства дифференциала.
- •55.Таблица дифференциалов.
- •60 Метод интегрирования «по частям» для вычисления неопределенного интеграла.
- •61 Интегралы, не выражающиеся через элементарные функции.
- •62 Задача нахождения площади криволинейной трапеции.
- •63 Определенный интеграл как предел интегральных сумм.
- •64 Производная определенного интеграла по верхнему пределу.
- •64.Теорема о производной определенного интеграла по переменному верхнему пределу
- •69. Определение несобственных интегралов с бесконечными пределами.
- •70. Несобственные интегралы от разрывных функций.
- •71. Интеграл вероятностей (Пуассона).
64.Теорема о производной определенного интеграла по переменному верхнему пределу
Интеграл
с переменным верхним пределом. Значение
определённого интеграла не зависит от
того, какой буквой обозначена переменная
интегрирования: 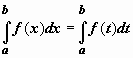 (чтобы
убедиться в этом, достаточно выписать
интегральные суммы, они совпадают). В
этом разделе переменную интегрирования
будем обозначать буквой t,
а буквой x обозначим
верхний предел интегрирования. Будем
считать, что верхний предел интеграла
может меняться, т.е. что x -
переменная, в результате интеграл будет
функцией Ф(x) своего
верхнего предела:
(чтобы
убедиться в этом, достаточно выписать
интегральные суммы, они совпадают). В
этом разделе переменную интегрирования
будем обозначать буквой t,
а буквой x обозначим
верхний предел интегрирования. Будем
считать, что верхний предел интеграла
может меняться, т.е. что x -
переменная, в результате интеграл будет
функцией Ф(x) своего
верхнего предела:  .
Легко доказать, что если f(t) интегрируема,
то Ф(x) непрерывна,
но для нас важнее следующая фундаментальная
теорема:
.
Легко доказать, что если f(t) интегрируема,
то Ф(x) непрерывна,
но для нас важнее следующая фундаментальная
теорема:
![]() Теорема
об интеграле с переменным верхним
пределом. Если
функция f(t) непрерывна
в окрестности точки t = x,
то в этой точке функция Ф(x) дифференцируема,
и
Теорема
об интеграле с переменным верхним
пределом. Если
функция f(t) непрерывна
в окрестности точки t = x,
то в этой точке функция Ф(x) дифференцируема,
и ![]() .
.
![]() Другими
словами, производная определённого
интеграла от непрерывной функции по
верхнему пределу равна значению
подынтегральной функции в этом
пределе.
Другими
словами, производная определённого
интеграла от непрерывной функции по
верхнему пределу равна значению
подынтегральной функции в этом
пределе.
![]() Док-во.
Дадим верхнему пределу x приращение
Док-во.
Дадим верхнему пределу x приращение ![]() .
Тогда
.
Тогда 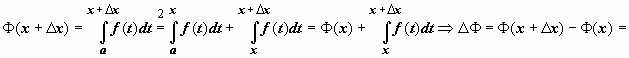
 ,
где c -
точка, лежащая междуx и
,
где c -
точка, лежащая междуx и ![]() (существование
такой точки утверждается теоремой о
среднем; цифры над знаком равенства -
номер применённого свойства определённого
интеграла).
(существование
такой точки утверждается теоремой о
среднем; цифры над знаком равенства -
номер применённого свойства определённого
интеграла). ![]() .
Устремим
.
Устремим ![]() .
При этом
.
При этом ![]() (c-
точка, расположенная между x и
(c-
точка, расположенная между x и ![]() ).
Так как f(t) непрерывна
в точке t = x,
то
).
Так как f(t) непрерывна
в точке t = x,
то![]() .
Следовательно, существует
.
Следовательно, существует ![]() ,
и
,
и ![]() .
Теорема доказана.
.
Теорема доказана.
Отметим
первое важное следствие этой теоремы.
По существу, мы доказали, что любая
непрерывная функция f(x) имеет
первообразную, и эта первообразная
определяется формулой  .
Другим важным следствием этой теоремы
является формула Ньютона-Лейбница, или
основная формула интегрального
исчисления.
.
Другим важным следствием этой теоремы
является формула Ньютона-Лейбница, или
основная формула интегрального
исчисления.
65. Формула Ньютона — Лейбница
Пусть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке.
Тогда

Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a).
66.Свойства определенного интеграла.
Свойства определенного интеграла:
1)

2) 
3) 
4)
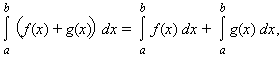
5)

Если
функция интегрируема на [a; b],
то она интегрируема на любом отрезке
![]()
Если
f (x)
– периодическая функция с периодом T,
то для любого a
|f (x)|
интегрируема на [a; b],
причем

67.Теорема о среднем значении определенного интеграла на отрезке
Пусть
функция f(x) непрерывна на
[a, b], тогда 
Доказательство:
1.
По свойству функции, непрерывной на
отрезке, ![]() ,
такие что
,
такие что ![]() .
.
2.
По свойству определенного
интеграла  ,
следовательно
,
следовательно  ,
, 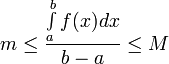 .
Обозначим дробь как m * .
.
Обозначим дробь как m * .
3.
Так как непрерывная функция принимает
все свои промежуточные значения, а ![]() ,
то
,
то ![]() ,
такая что
,
такая что 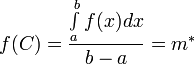
68. Геометрические приложения определенного интеграла.
Вычисление площадей плоских фигур
Известно,
что определенный интеграл на отрезке
представляет собой площадь криволинейной
трапеции, ограниченной графиком
функции f(x).
Если график расположен ниже оси Ох,
т.е. f(x)
< 0, то площадь имеет знак “-“, если
график расположен выше оси Ох, т.е. f(x)
> 0, то площадь имеет знак “+”.
Для
нахождения суммарной площади используется
формула: .
.
Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенных интегралов, если известны уравнения этих линий.
Пример. Найти площадь фигуры, ограниченной линиями y = x, y = x2, x = 2 Искомая площадь может быть найдена по формуле:
 (ед2)
(ед2)
Площадь
фигуры, ограниченной кривыми y=f1(x)
и y=f2(x),
[f1(x)≤f2(x)]
и прямыми х=а и х=b,
находится по формуле:![]()
Пример.
Вычислить площадь фигуры, ограниченной
заданными линиями y=–x2, y=–x–2.
Решение.
Найдем абсциссы
точек пересечения данных
линий:
x1=–1,x2=2.
Значит,
![]()
![]() =–3+1,5+4+2=4,5.
=–3+1,5+4+2=4,5.
Объем
тела, полученного вращением криволинейной
трапеции вокруг оси Ох;
находится по формуле: ![]()
Длина кривой, заданной уравнением y=f(x), a ≤x≤b,выражается следующим образом:

