
1 |
Понятие числового ряда. Критерий Коши. Необходимое и достаточное условие сх-ти рядов с неотр. членами. |
![]() .
.
![]() -
ЧР (1). Член ряда, n-ая частичная сумма.
-
ЧР (1). Член ряда, n-ая частичная сумма.
ЧР сх-ся, если посл. Sn
его част. сумм сх-ся:
![]() -
сумма ряда. Не сущ. – расходится.
-
сумма ряда. Не сущ. – расходится.
S-Sn=rn – n-ый остаток ЧР. Пр.: qk-1, ex.
Т1. Крит. Коши. Для того чтобы ЧР(1)
сх-ся
люб. ε>0 сущ N: люб n>N, люб p из R:
![]() .
.
Cл. Для того чтобы (1) сх-ся необх., чтобы Uk=о(1) k→∞. (из теор при р=1). Пр. ∑1/k - гарм. ряд.
Зам1. Добавл. или отбрас. конечн.
числа слаг в ЧР не влияет на его сх-ть
или расх-ть. (=> из крит для: n>>1 эти
слаг не попадут в
![]() ).
Зам2. Для люб С<>0 ряды
).
Зам2. Для люб С<>0 ряды
![]() и
и
![]() сх-ся
или расх одновременно.
сх-ся
или расх одновременно.
Т2. Для того чтобы ЧР
![]() с
неотр членами сх-ся чтобы
посл {Sn} его част сумм была огр.
Д-во. <=: ряд сх-ся→{Sn} сх→{Sn}
огр. =>: {Sn} огр, pk>=0→Sn
не убыв→{Sn}
сх→ряд сх-ся.
с
неотр членами сх-ся чтобы
посл {Sn} его част сумм была огр.
Д-во. <=: ряд сх-ся→{Sn} сх→{Sn}
огр. =>: {Sn} огр, pk>=0→Sn
не убыв→{Sn}
сх→ряд сх-ся.
2 |
Признаки сходимости рядов с неотрицательными членами. |
∑pk (1), ∑pk' (2) p>=0
1 пр сравнения. Пусть, начиная с некот номера n0, вып неравенство pk<=pk', k>=n0 (3)=> из сх (2)→сх (1); из расх (1)→расх (2). Д-во. 1. Пусть (3) вып для люб k →Sn<=Sn'; {Sn} огр→{Sn'}огр. 2. от противного из 1.
Зам. Верно и для pk<=сpk'. Пр. ∑1/ka, a<1.
2 пр сравнения. pk>0 k>=k0. Пусть сущ конечный и <>0 lim(pk'/pk)=L => (1), (2) сх и расх одновр. Д-во. сущ lim(pk'/pk)=L >0 =>люб ε>0 сущ N>k0: люб k>=N L-ε<pk'/pk<L+ε, ε>L=>*pk=>из Т1.
3 пр сравнения. pk, pk' >0 k>=k0. Пусть pk+1/pk<=pk+1'/pk' люб k>=k0. Тогда сх(2)=>сх(1), расх(1)=>расх(2). Д-во. Пусть верно для люб k. Перемножим нер-ва k от 1 до n-1: pn/p1<=pn'/p1'→*p1→Т1.
∑pk (1) сравн с ∑qk-1
q![]() (0;1) и ∑1.
(0;1) и ∑1.
Пр. Коши. 1. Пусть
![]() <=q<1
(
>=1)
люб k>=k0>=1
=>(1) сх (расх). 2. Пусть сущ lim
=L
=> L<1 →(1) сх, L>1
→(1) расх. Д-во. 1.
<=q<1→pk<=qk,
q
(0;1);
>=1
→pk не→0. 2. Расписываем предел,
L<1→0<ε<1-L,
q=L+ε→п1;
L>1→ε=L-1→п1.
<=q<1
(
>=1)
люб k>=k0>=1
=>(1) сх (расх). 2. Пусть сущ lim
=L
=> L<1 →(1) сх, L>1
→(1) расх. Д-во. 1.
<=q<1→pk<=qk,
q
(0;1);
>=1
→pk не→0. 2. Расписываем предел,
L<1→0<ε<1-L,
q=L+ε→п1;
L>1→ε=L-1→п1.
Пр. Даламбера. pk>0,k>=k0. 1. Пусть pk+1/pk<=q<1 (pk+1/pk>=1) люб k>=k0>=1 =>(1) сх (расх). 2. Пусть сущ lim(pk+1/pk)=L => L<1 →(1) сх, L>1 →(1) расх. Д-во. 1. pk+1/pk<=q=qk+1/qk, q (0;1) →3 пр сравн.; pk+1/pk>=1 →pk не→0. 2. Расписываем предел, L<1→0<ε<1-L, q=L+ε→п1; L>1→ε=L-1→п1.
Зам1. <=q<1 нельзя заменить на <1 (∑1/k). Зам2. При L=1 признаки не работают. (∑1/k и ∑1/k2).
Зам. Обобщ. Т1 и Т2. Верхний предел <1 =>сх. Д-во. <L+ε, ε=(1-L)/2→q=L+ε<1→из п2.
Утв. Коши сильнее Даламбера. Сущ
lim(pт+1/pт)=L
=> сущ lim![]() =L.
Обратное не верно.
=L.
Обратное не верно.
Лемма. 1. an→a
=> (a1+…+an)/n→a.
2. an>0,
an→a
=>
![]() →a.
Д-во. 1. люб. ε>0 сущ N:
люб n>N
|an-a|<ε/2.
(a1+…+an)/n-a=((a1-a)+…+(aN-a))/n+((aN+1-a)+…+(an-a))/n<ε
люб n>=N1,
т к при
дост большом
N1
певая дробь
<ε. 2.
ln непр =>lnan→lna;
п1, ln
=(lna1+…+lnan)/n→lna.
→a.
Д-во. 1. люб. ε>0 сущ N:
люб n>N
|an-a|<ε/2.
(a1+…+an)/n-a=((a1-a)+…+(aN-a))/n+((aN+1-a)+…+(an-a))/n<ε
люб n>=N1,
т к при
дост большом
N1
певая дробь
<ε. 2.
ln непр =>lnan→lna;
п1, ln
=(lna1+…+lnan)/n→lna.
Д-во.
![]() →L.
Пр.
→L.
Пр.
![]() .
.
Пр Коши-Маклорена. Рассм невозр
f(x)>=0 на
x>=1. Тогда для сх-ти ЧР
![]()
сх-сь числ посл {an},
сх-сь числ посл {an},
![]() ,
т.е. сх-ся
,
т.е. сх-ся
![]() .
Д-во. Фикс k>=2 и рассм x
[k-1,k];
f(x)↓→f(k)<=f(x)<=f(k-1);
f(x) монот,
огр →инт-м на [k-1,k]
и суммируем по k
[1,n].
.
Д-во. Фикс k>=2 и рассм x
[k-1,k];
f(x)↓→f(k)<=f(x)<=f(k-1);
f(x) монот,
огр →инт-м на [k-1,k]
и суммируем по k
[1,n].
![]() =>Sn-f(1)<=an<=Sn-1.
{an}
неуб=> она сх-ся
огр., ЧР сх-сяогр {Sn},
а их огр одновременна.
=>Sn-f(1)<=an<=Sn-1.
{an}
неуб=> она сх-ся
огр., ЧР сх-сяогр {Sn},
а их огр одновременна.
Зам. [1,∞)→[m,∞), m
– натуральное,
![]() ,
,
![]() .
Пр.
.
Пр.
![]() ,
,
![]() .
.
3 |
Теоремы Коши и Римана о перестановке членов в числовых рядах. |
Абс сх-ся ЧР. Утв. ЧР сх-ся абс => он сх-ся. (расписать крит Коши). Усл сх-ся ЧР.
Переместительное св-во. Пр. ∑(-1)k-1/k (перест члены тройками, Hn=lnn+c+an→S'=1/2*S).
Т. Римана. Пусть ЧР сх-ся усл, тогда для любого L можно так перест слагаемые ЧР, что вновь получ ряд будет иметь S=L. Д-во. pk – неотр члены, qk – модули отр членов в том же порядке.
Утв. Чисел {pk}и{qk} беск много (иначе ЧР сх-ся абс). P≈∑pk, Q≈∑qk.
Утв. P,Q – расх. Д-во. Sn=Pn-Qn. От противного: P сх-ся→Qn=Sn-Pn→Q сх-ся→|ЧР|=P+Q →ЧР сх-ся абс.
И для Р, и для Q после удал конечн числа слаг из ост слаг можно выбрать столько, что их сумма > люб числа.
Фикс L. Построим ∑U'k: (ровно необход кол-во) pk →S>L, qk→S<L и т.д. (войдут все члены ЧР, т.к. на каждом шаге добавл хотя бы одно слаг).
∑U'k=L? S'n из последовательных групп полож и отр слаг. S'n оканч заверш группой→|S'n-L|<=pkl – последнего слаг в группе; S'n оканч незаверш группой→посл слаг в предпосл группе => д-жем, что посл последних слаг б/м: pk, qk – б/м (необх усл сх-ти исх ЧР)→{pki,qkj} – б/м. => S'n→L.
Зам. L→+- ∞ - верно.
Т. Коши. Пусть ЧР сх-ся абс, тогда люб
ряд, получ из данного путем некот перест
слаг сх-ся абс и имеет ту же сумму. Д-во.
ЧР сх-ся абс => люб ε>0 сущ N0:
![]() =ε/2.
∑U'k
получен из исх путем перест слаг.
=ε/2.
∑U'k
получен из исх путем перест слаг.
Д-ть: 1. ∑U'k
сх-ся и имеет сумму S, 2. он сх-ся абс.
1. Фикс N настолько
большим, что все первые N0 слаг
содерж в S'n (n>=N). люб n>=N
|S'n-S|<=|S'n-![]() |+|
-S|<
+
<ε.
2. аналогично п1.
|+|
-S|<
+
<ε.
2. аналогично п1.
4 |
Признаки сх-ти произвольных числовых рядов. |
ЧП {Vk} наз посл с огр изменениями,
если сх-ся ЧР
![]() .
Пр. Vk=k, Vk=1/k, Vk=(-1)k-1/k.
.
Пр. Vk=k, Vk=1/k, Vk=(-1)k-1/k.
Утв1. Если {Vk} имеет огр измен, то она сх-ся. Д-во. ЧР сх-ся=>сх-ся и без модулей=>Sn=Vn+1-V1→S.
Утв2. Всякая монот и огр посл имеет
огр измен. Д-во. Vn→V.
ЧР: Sn=
=
=![]() =|Vn+1-V1|→|V-V1|
=> Sn
сх-ся.
=|Vn+1-V1|→|V-V1|
=> Sn
сх-ся.
Утв3. Для того чтобы {Vn} имела огр измен чтобы общий член Vn можно было представить в виде разности двух неуб огр посл Vn=Un-Wn.
Тождество Абеля (преобразования).
{Uk},
{Vk},
Sn=![]() ,S0=U0=0,
,S0=U0=0,
![]() n,p
n,p![]() :
:
![]()
![]() . Д-во. Uk=Sk-Sk-1,
. Д-во. Uk=Sk-Sk-1,
![]()
![]() заданному.
заданному.
Рассмотрим![]() (1),Sn=
.
(1),Sn=
.
1 пр. Абеля. Если {Sn} огр и {Vk}
- б/м посл с огр измен, то (1) сх-ся. Д-во.
![]() М=const>0:
|Sn|<=M,
n.
ε>0
N:
k>N
|Vk|<ε/(4M).
ε>0
N:
n>N,
p
М=const>0:
|Sn|<=M,
n.
ε>0
N:
k>N
|Vk|<ε/(4M).
ε>0
N:
n>N,
p
![]() <ε/(2M).
Тожд Абеля→
<ε/(2M).
Тожд Абеля→
![]() <ε,
n→(1)
сх-ся.
<ε,
n→(1)
сх-ся.
2 пр Абеля. Если
![]() сх-ся
и {Vk} - посл с огр измен, то (1) сх-ся.
Д-во. {Sn} огр →
М=const>0:
|Sn|<=M,
n.
S:
=S.
V:
Vk→V.
ε>0
N:
n>N,
p
<ε/(2M).
Тожд Абеля→{Sn+pVn+p-SnVn+1→SV-SV=0}→
<ε,
n→(1)
сх-ся.
сх-ся
и {Vk} - посл с огр измен, то (1) сх-ся.
Д-во. {Sn} огр →
М=const>0:
|Sn|<=M,
n.
S:
=S.
V:
Vk→V.
ε>0
N:
n>N,
p
<ε/(2M).
Тожд Абеля→{Sn+pVn+p-SnVn+1→SV-SV=0}→
<ε,
n→(1)
сх-ся.
Пр. Дирихле-Абеля. Если {Sn} огр и {Vk} – невозр б/м посл, то (1) сх-ся. Д-во. {Vk} сх-ся→огр, монот => {Vk} с огр измен. 1 пр Абеля.
Пр. Лейбница. Рассм знакоперем ряд
![]() ,
pk>0, {pk} – невозр б/м посл.
Такой ряд сх-ся. Д-во. Uk=(-1)k,
Vk=pk,
пр Дирихле-Абеля.
,
pk>0, {pk} – невозр б/м посл.
Такой ряд сх-ся. Д-во. Uk=(-1)k,
Vk=pk,
пр Дирихле-Абеля.
5 |
Арифметические операции над сх-ся ЧР. Теорема Мертенса. |
Рассмотрим сх-ся ряды
![]() =V,
=V,
![]() =U,
uk,vk
R,
част суммы Vn,Un.
(1)
=U,
uk,vk
R,
част суммы Vn,Un.
(1)
Т1. Если ряды (1) сх-ся , V,U, то
![]() сх-ся и его сумма V+-U. Д-во.
сх-ся и его сумма V+-U. Д-во.
![]() .
.
Т2. Если ряды (1) сх-ся абс, V,U, то ряд,
составленный из всевозм произвед вида
uk*vl, k,l
N,
занумерованных в произв порядке, сх-ся
абс и его сумма VU. Д-во. 1. Абс сх-ть.
wk=um*vl,
![]() .
.
p – наиб из номеров k и l,
вход в Sn. Sn<=(|u1|+…+|up|)(|v1|+…+|vp|)→{![]() ,
,
![]() - огр}→{Sn}
огр→
сх-ся. 2.
- огр}→{Sn}
огр→
сх-ся. 2.
![]() =UV.
Ряд сх-ся абс →его слаг можно переставлять
– сумма не изменится→Wn=(u1+…+un)(v1+…+vn)=UnVn→UV.
=UV.
Ряд сх-ся абс →его слаг можно переставлять
– сумма не изменится→Wn=(u1+…+un)(v1+…+vn)=UnVn→UV.
Правило Коши. ( )( )=u1v1+(u1v2+u2v1)+…+(u1vk+…+ukv1)+…= .
Т Мертенса. Если один из (1) сх-ся абс, а второй хотя бы усл, то ряд, полученный перемнож рядов (1) по правилу Коши сх-ся и его сумма UV. Д-во. . - усл, - абс. n= V-0 => M=const>0: |n|<=M, n. Wn=u1(v1+v2+…+vn)+u2vn-1+…+unv1={Vn=V-n}=U1(V-n)+U2(V-n-1)+…+
+un(V-1)=UnV-n, n=u1n+u2n-1+…+un1.
UnVUV=>
достаточно доказать, что n=![]() (1).
(1).
Ряд сходится абсолютно => M1=const>0 : <=M1, n.
>0 m: </2M. n0 => n1: n>n1 |n|< /2M1.
n>m n=(u1n+u2n-1+….+umn-m+1)+(um+1n-m+un1)
n>m+n1 => справедливы все выше указанные оценки : |n|<=|…|+|…|</2M1*+M < M1*/2M1+M*/2M= => n0, n беск. и =UV.
6 |
Бесконечные произведения, критерии сх-ти. |
Рассмотрим ЧП
![]() :
:
![]() (1) – беск произвед.
(1) – беск произвед.
Беск. произв. называется сх-ся, если
последовательность
![]() его частичных произведений имеет
конечный предел != 0, при n→0.
его частичных произведений имеет
конечный предел != 0, при n→0.
Т (необх усл сх-ти беск.произв.). Для
того чтобы б.пр. (1) сходилось необх, чтобы
Vk→1,
k→∞. Д-во.
![]() ,
,
![]() .
.
Далее рассматриваем Vk > 0.
Зам. добавление или отбрасывание из б.пр. (1) конечного числа первых сомн. (!=0) не влияют на сх-ть или расх-ть б.пр.(1).
Т. б.пр.(1) с Vk
> 0 сх-ся сх-ся ЧР![]() (2).
Д-во.
(2).
Д-во.
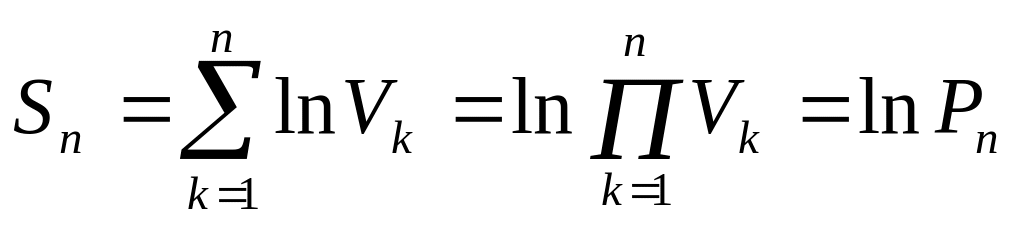
![]()
<=> для сх-ти {Pn},
т.е. (1) <=> cх-ть {Sn},
т.е. (2). Pn=eSn,
n![]() ; P=eS
; P=eS
Сл. Необх усл сх-ти => сх-ть (1) <=>
сх-ть ряда
![]() .
.
Т. Рассмотрим беск.пр.
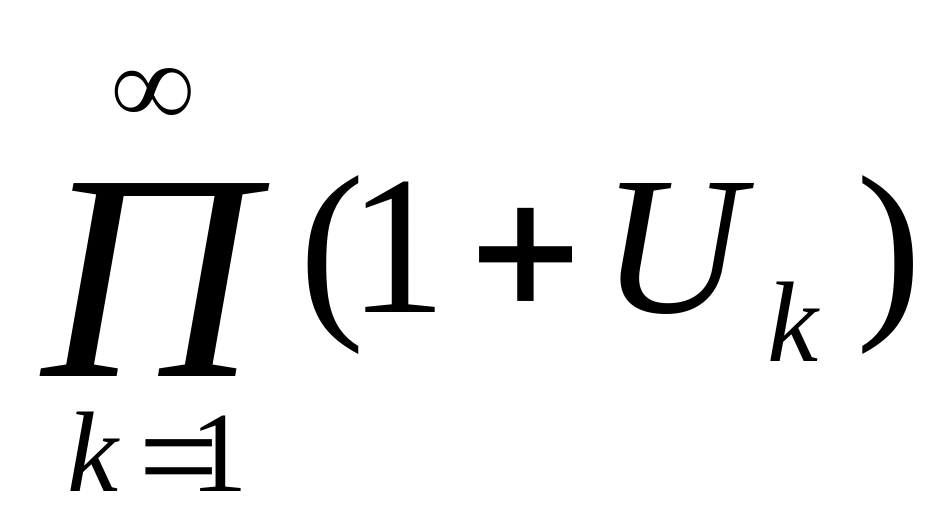 (5). Пусть Uk
– сохраняет знак (Uk>-1).
Тогда (5) сх-ся <=>сх-ся ряд
(5). Пусть Uk
– сохраняет знак (Uk>-1).
Тогда (5) сх-ся <=>сх-ся ряд
![]() (6). Д-во. Uk0
– необх усл сх-ти и (5) и (6). => Пусть Uk0
и ln(1+Uk)-сохр.знак.
(6). Д-во. Uk0
– необх усл сх-ти и (5) и (6). => Пусть Uk0
и ln(1+Uk)-сохр.знак.
Тогда
![]() => (5) и (6) сходятся и расходятся
одновременно.
=> (5) и (6) сходятся и расходятся
одновременно.
7 |
Двойной ряд: необх усл сх-ти, связь со сх-тью повторного ряда, кр сх-ти ряда с неотр членами. |
Матрица с беск числом столбцов и строк.
![]() -
повторный ряд. Сх-ся, если сх-ся все
ряды по строкам
-
повторный ряд. Сх-ся, если сх-ся все
ряды по строкам
![]() и сх-ся ЧР
и сх-ся ЧР
![]() .
.
![]() -двойной
ряд. Сх-ся, если сущ двойн lim мн-ва част
прямоуг сумм
-двойной
ряд. Сх-ся, если сущ двойн lim мн-ва част
прямоуг сумм
![]() :
:
![]() .
.
Утв. akl=bk*cl,
![]() ,
,![]() -
сх-ся, то двойной ряд сх-ся.
-
сх-ся, то двойной ряд сх-ся.
Необх усл сх-ти.
![]() .
Д-во.
amn=(Smn-S(m-1)n)-(Sm(n-1)-S(m-1)(n-1))→(S-S)-(S-S)=0.
.
Д-во.
amn=(Smn-S(m-1)n)-(Sm(n-1)-S(m-1)(n-1))→(S-S)-(S-S)=0.
![]() (1),
(1),
![]() (2),
(3),
(2),
(3),
![]() (4),
(5)
(4),
(5)
Т. Пусть сх-ся все ряды по строкам
(2) матрицы и сх-ся двойной ряд (5). Тогда
сх-ся и повт ряд (3) и его ∑=∑(5). Д-во.
.
(2) сх-ся =>
![]() =>
∑(3)(предел правой части при m→∞) = повт
пределу
=>
∑(3)(предел правой части при m→∞) = повт
пределу
![]() =>
д-ем сущ повт предела и его = ∑(5). Cх-ся
(5) => люб ε>0 сущ натур m0, n0: люб m>m0,
n>n0 |Smn-S|<ε/2 => S-ε/2<=
=>
д-ем сущ повт предела и его = ∑(5). Cх-ся
(5) => люб ε>0 сущ натур m0, n0: люб m>m0,
n>n0 |Smn-S|<ε/2 => S-ε/2<=![]() <=S+ε/2
=> |φm-S|<=ε/2<ε
=> чтд
<=S+ε/2
=> |φm-S|<=ε/2<ε
=> чтд
Т'. Пусть сх-ся все ряды по столбцам (1) матрицы и сх-ся (5). Тогда сх-ся и повт ряд (4) и его ∑=∑(5).
Кр. сх-ти. Двойной ряд (5) с неотр членами сх-ся мн-во {Smn} ограничено. Д-во. => Smn<S люб m,n, тк akl>=0. <= сущ supSnm=S → люб ε>0 сущ Sm0n0 из {Smn}: S-ε<Sm0n0<=S. akl>0 → люб m>m0, n>n0 Smn>=Sm0n0 → S-ε<Sm0n0<=Smn<S → сущ .
8 |
Абс сх-ть двойного ряда. Взаимосвязь между сх-тью повторных, двойного и одинарного рядов. |
Двойной ряд сх-ся абс, если сх-ся
![]() (5").
(5").
Т. Сх-ть (5") => сх-ть (5). Д-во. Рассмотрим мн-ва pkl=(|akl|+akl)/2, 0<=pkl<=|akl|, qkl=(|akl|-akl)/2, 0<=qkl<=|akl|. (5") сх-ся => {Smn} его част сумм ограничено => част суммы двойных рядов с pkl и qkl огр => эти ряды сх-ся => (5) сх-ся как их разность.
![]() (6)
составлен из элементов матрицы,
занумерованных в произвольном порядке.
(6)
составлен из элементов матрицы,
занумерованных в произвольном порядке.
Т. Если хотя бы один из рядов (3")-(6") сх-ся, то сх-ся все ряды (3)-(6) и суммы их одинаковы.
Д-во. Рассматриваем (3), для (4) аналогично.
1. (3")=>(6")=>(6). S, Smn –
сумма и част сумма (3") => Smn<=S
люб m,n. Фикс люб натур р и
![]() .
m,n настолько большие, что
все ar,
r<p содержатся
в Smn
=> Sp<=Smn<=S
люб р => (6") и (6) сх-ся.
.
m,n настолько большие, что
все ar,
r<p содержатся
в Smn
=> Sp<=Smn<=S
люб р => (6") и (6) сх-ся.
2. (6")=>(5")=>(5). Фикс люб m,n. Сущ настолько большой р, что все эл-ты Smn входят в Sp => Smn<=Sp<=S люб m,n, S – сумма (6") => (5") и (5) cх-ся.
3. (5")=>(3"), (5")=>(3). (5) сх-ся абс => част суммы (2") огр суммой (5") => (2") и (2) сх-ся. (5") и (2") сх-ся => (3") сх-ся. (5") сх-ся => (5) сх-ся, (2) сх-ся => (3) сх-ся и его ∑=∑(5).
(6) и (5) имеют одинаковые суммы: (5) сх-ся абс=> от перестановки членов сумма не изменяется => суммы одинаковы.
9 |
Обобщенные методы суммирования расходящихся рядов (Чезаро, Пуассона-Абеля). |
![]() (1) Сходится, если сходится SnS,
где S – сумма ряда.
(1) Сходится, если сходится SnS,
где S – сумма ряда.
Требования: Регулярность: если
(1) сходится, его сумма S,
то он имеет и обобщенную сумму S.
Линейность метода:
~Uоб
– обобщенная сумма,
![]() ~Vоб
. {
~Vоб
. {![]() }
=>
}
=>
![]()
Метод Чезаро (метод средних
арифметических):
![]() (2).
(2).
![]() - обобщенная сумма (по Чезаро) (1).
Линейность:
~Uоб;
Un=
;
- обобщенная сумма (по Чезаро) (1).
Линейность:
~Uоб;
Un=
;
![]() ~
(2);
~Vоб;
Vn=
;
~
(2);
~Vоб;
Vn=
;
![]() ~
(2)
~
(2)
![]() :
:
![]() ,
Sn,
,
Sn,
![]() ~
(2) :
=
~
(2) :
=![]()
Регулярность : следует из леммы о сходимости последовательности средних арифметических: SnS => {лемма}=> S
Метод Пуассона-Абеля: Пусть ряд (1)
сходится
![]() ,
его сумма S(x),
пусть
,
его сумма S(x),
пусть
![]() = Sоб. Тогда ряд
называется суммируемым по методу
Пуассона-Абеля и число Sоб
называется его обобщенной суммой (по
Пуассону-Абелю).
= Sоб. Тогда ряд
называется суммируемым по методу
Пуассона-Абеля и число Sоб
называется его обобщенной суммой (по
Пуассону-Абелю).
Линейность:
![]() ,
,
![]() ,
{
}
=>
,
{
}
=>
![]()
Регулярность: Пусть
![]() =S.
Доказать: 1.
=S.
Доказать: 1.
![]() -
сходится, S(x).
2.
= S
-
сходится, S(x).
2.
= S
1.
-сходится
=> Uk=![]() (1)=>
{Uk}-ограничена:
(1)=>
{Uk}-ограничена:
![]()
![]() .
.
![]() -
сх-ся
→
(1) сх-ся абс
→S(x)
– сумма ряда (1),
-
сх-ся
→
(1) сх-ся абс
→S(x)
– сумма ряда (1),
2. S(x)=
, S=
,
Sn=![]() ;
SnS;
rn=S-Sn0.
Тождество Абеля:
;
SnS;
rn=S-Sn0.
Тождество Абеля:
![]() (S0=0,
Vn=xn-1,
n=1, pбеск,
Sn+pS,
Vn+p0,
Sn-1=0,
Vn0)
=> S(x)=
(S0=0,
Vn=xn-1,
n=1, pбеск,
Sn+pS,
Vn+p0,
Sn-1=0,
Vn0)
=> S(x)=![]() ;
;
![]() =>
=>
![]() =>
=>
![]() ,
rk0
=>
,
rk0
=>
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
т.е.
,
т.е.
![]() =>
=>
=> S(x)
![]() ,
ч.т.д.
,
ч.т.д.
10 |
ФП и ФР. Равномерная сх-ть. Кр Коши. |
{x}из Rm, натур n → {fn(x)} – ФП. ФП {Un(x)} → ∑Un(x) – ФР.
ФП {fn(x)} сх-ся в x0 из {x}, если сх-ся ЧП {fn(x0)}. {x"} – м-во точек сх-ти => пред ф-ция f(x) на {x"}.
ФР ∑Un(x) сх-ся в x0 из {x}, если сх-ся ЧР ∑Un(x0). {x"} – м-во точек сх-ти => сумма S(x) на {x"}.
ФП и ФР сх-ся на мн-ве, если они сх-ся в каждой точке этого мн-ва.
Опр. ФП равн сх-ся на {x}, если люб ε>0 сущ номер, начиная с которого |fn(x)-f(x)|<ε для всех х из {x}.
Кр. fn(x) равн сх-ся к f(x)
![]() .
Д-во. Расписать опр равн сх-ти и
предела.
.
Д-во. Расписать опр равн сх-ти и
предела.
Зам. Из сх-ти не следует равн сх-ть (∑xk на [0,1]).
Опр. ФР равн сх-ся на {x}, ФП его частичных сумм {Sn(x)} сх-ся равн на {x}.
Кр Коши. ФП сх-ся равн на {x} люб ε>0 сущ N: люб n>N, люб натур р и люб х из {x} |fn+p(x)-fn(x)|<ε. Д-во. => равн сх-ть => люб n,x |fn(x)-f(x)|<ε/2 => люб p |fn+p(x)-f(x)|<ε/2 => суммируем. <= по кр Коши для ЧП (при каждом фикс х) => ФП fn(x)→f(x). |fn+p(x)-fn(x)|<ε/2, p к бесконечности => |f(x)-fn(x)|<=ε/2.
Кр Коши.
ФР сх-ся равн на {x}
люб ε>0 сущ N: люб n>N,
люб натур р и люб х из {x}
![]() <ε.
<ε.
11 |
Признаки равн. сходимости ФР. |
Признак Вейерштрасса. Если функц.
ряд ![]() определен на {x} пространства
определен на {x} пространства
![]() и если существует сходящийся ряд
и если существует сходящийся ряд ![]() такой что для всех точек {x}
и для всех номеров k
справедливо
такой что для всех точек {x}
и для всех номеров k
справедливо ![]() ,
то функц. ряд
равномерно
сходится на {x}. Д-во.
,
то функц. ряд
равномерно
сходится на {x}. Д-во.
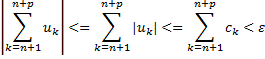
По критерию Коши ряд сходится. Чтд.
Послед. ![]() называется равномерно ограниченной на
{x}, если существует такое
вещественное число M>0,
что для все n и для всех
точек x
называется равномерно ограниченной на
{x}, если существует такое
вещественное число M>0,
что для все n и для всех
точек x ![]() .
.
Послед. ![]() называется последовательностью,
обладающей на множестве {x}
равномерно ограниченным изменением,
если функц. ряд
называется последовательностью,
обладающей на множестве {x}
равномерно ограниченным изменением,
если функц. ряд ![]() сходится равномерно на множестве {x}.
сходится равномерно на множестве {x}.
Последовательность, обладающая на
множестве {x} равномерное
ограниченным изменением, сходится
равномерно на множестве {x}к
некоторой предельной функции. Из
равномерной сходимости ряда с модулями
вытекает равномерная сходимость ![]() ,
n-я частичная сумма которого
,
n-я частичная сумма которого
![]() .
Отсюда вытекает равномерная сходимость
к
.
Отсюда вытекает равномерная сходимость
к ![]() .
.
1 признак Абеля. Если ![]() обладает равномерно ограниченной
последов. частичных сумм, а
обладает равномерно ограниченной
последов. частичных сумм, а ![]() обладает равномерное ограниченным
изменением, и имеет предельную функцию,
тожд. равную нулю. , то функ. ряд
обладает равномерное ограниченным
изменением, и имеет предельную функцию,
тожд. равную нулю. , то функ. ряд ![]() равномерно сходится (для всех св-в мн-во
{X}). Д-во.
равномерно сходится (для всех св-в мн-во
{X}). Д-во.
![]() Фиксируем
Фиксируем ![]() ;
; ![]() ,
, ![]()
По тождеству Абеля
![]()
Равномерно сходится по критерию Коши.
2 признак Абеля. Если ![]() сх-ся равномерно, а
сх-ся равномерно, а ![]() обладает ограниченным изменением и
явл. равномерно ограниченной, то
обладает ограниченным изменением и
явл. равномерно ограниченной, то ![]() сх-ся
равномерно. Д-во. Возьмем
сх-ся
равномерно. Д-во. Возьмем ![]() .
Фиксируем
.
Фиксируем ![]() Возьмем и отбросим первые
Возьмем и отбросим первые ![]() .
(Можем в силу замечания). Отбросим у
рядов
.
(Можем в силу замечания). Отбросим у
рядов![]() первые
N членов. Это не повлияет
на их равномерную сходимость. В силу
равномерной сходимости
первые
N членов. Это не повлияет
на их равномерную сходимость. В силу
равномерной сходимости ![]()
![]()
Следствие (признак Дирихле-Абеля).
Если ![]() обладает равномерно ограниченной посл.
част. сумм, а
не возрастает в каждой точке {x}
и равномерно сходится к 0, то
равн.
сх-ся. Д-во.
обладает равномерно ограниченной посл.
част. сумм, а
не возрастает в каждой точке {x}
и равномерно сходится к 0, то
равн.
сх-ся. Д-во. ![]()
12 |
Признак Дини равномерной сходимости ФР и ФП. Почленный переход к пределу, непрерывность. |
Признак Дини
Если
не убывает (не возр) в каждой точке
замкнутого огр. мн-ва {x}
и сходится к ![]() ,
и если
,
и если ![]() непрерывны, то сходимость равномерна.
Д-во.
непрерывны, то сходимость равномерна.
Д-во.
Не огр. общности ![]() не возр.
не возр. ![]() .
.
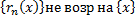
 =0
=0
Пусть не сх-ся равномерно. Тогда ![]() .
В силу огр. {x} по т.
Больцано-Вейерштрасса можно выделить
.
В силу огр. {x} по т.
Больцано-Вейерштрасса можно выделить
![]() .
.
![]() в силу непр
в силу непр
![]()
Т*. Если все члены ряда неопр. и неотр. (непол) на замкнут. огр. мн-ве и в кажд. точке ряд сходится, и его сумма непр., то сх-ть равномерна.
Т. Если
сх-ся равномерно на {x} к
S(x) и у всех
членов сущ. предел в ![]() ,
то и сумма S(x)
имеет в точке
предел
,
то и сумма S(x)
имеет в точке
предел ![]() .
Д-во.
.
Д-во.
Сначала докажем сходимость ![]() Перейдем к пределу
Перейдем к пределу ![]() .
По кр. Коши
.
По кр. Коши ![]()
Оценим разность ![]()
Фиксируем ![]() .
.
Можно указать ![]() для точек
для точек ![]() .
Это доказывает существ. предела.
.
Это доказывает существ. предела.
Можно переформулировать в терминах последовательности.
Следствие1. Если потребовать, чтобы принадлежала {x}, а все члены ряда были непрерывны, то и сумма будет непрерывна.
Следствие2. Если вче члены ряда(посл) непрерывны на плотном в себе мн-ве {x}, и если функц. ряд (посл) сх-ся равномерно на {x}, то и сумма ряда (пред. функц.) непрерывна на {x}.
13 |
Почленное диффер., сущ первообразных для ФП и ФР. |
Т. Если каждая ![]() имеет производную на сегменте, причем
послед. производных сх-ся равн на нем,
а сама
имеет производную на сегменте, причем
послед. производных сх-ся равн на нем,
а сама ![]() сх-ся
хотя бы в одной точке сегмента, то
равн сх-ся к некоторой пред.
на сегменте, причем послед. можно
дифференцировать почленно. Д-во.
Докажем равн. сходимость посл. на
сегменте. Из сходимости в точке и равн.
сход-ти следует
сх-ся
хотя бы в одной точке сегмента, то
равн сх-ся к некоторой пред.
на сегменте, причем послед. можно
дифференцировать почленно. Д-во.
Докажем равн. сходимость посл. на
сегменте. Из сходимости в точке и равн.
сход-ти следует
![]()
По теореме Лагранжа ![]()
Отсюда ![]() - равн сх-ть.
- равн сх-ть.
Докажем существование производной.
Фиксируем произвольное ![]() ,
чтобы она содержалась целиком в нашем
отрезке. Обозначим
,
чтобы она содержалась целиком в нашем
отрезке. Обозначим ![]() ,
, ![]()
В силу равн сх-ти ![]()
По т. Лагранжа ![]()
![]() равномерно сходится. Поэтому по теорм.
почленном пред. переходе в
равномерно сходится. Поэтому по теорм.
почленном пред. переходе в ![]() .
Согласно этой теореме функция
.
Согласно этой теореме функция ![]() являющ. пред. функцией послед. имеет
предел в
являющ. пред. функцией послед. имеет
предел в ![]()
![]() ч.т.д.
ч.т.д.
\
В терминах ФР: если каждая ![]() имеет произв. на [a,b],
и если ряд из производных равн сх-ся на
[a,b], а сам
ряд сходится хотя бы в одной точке
,
то последний ряд сх-ся равн на [a,b]
к некоторой сумме S(x),
причем этот ряд можно диффер. на [a,b]
почленно, т.е. его сумма имеет производную,
являющ. суммой ряда из проиводных.
имеет произв. на [a,b],
и если ряд из производных равн сх-ся на
[a,b], а сам
ряд сходится хотя бы в одной точке
,
то последний ряд сх-ся равн на [a,b]
к некоторой сумме S(x),
причем этот ряд можно диффер. на [a,b]
почленно, т.е. его сумма имеет производную,
являющ. суммой ряда из проиводных.
Т. Если каждая имеет первообр. на [a,b], сходится равномерно на [a,b] к предельной f(x), то и f(x) имеет первообр. на [a,b]. Д-во. {gn(x)} – посл первообр для {fn(x)} на [a,b]. {fn(x)} cх-ся равн => {g'n(x)} сх-ся равн на [a,b]. Сх-ть в x0? фикс люб х0 из [a,b) => φn(x)=gn(x)-gn(x0) => φ'n(x)=g'n(x)=fn(x) равн сх-ся к f(x), φn(x0)=0 люб n (а значит φn(x) сх-ся) => φn(x) сх-ся равн к φ(х), сущ φ'(x)=limφ'n(x)=f(x) => сущ φ: φ'(x)=f(x), т.е. f(x) имеет первообр.
ФР: Пусть ФР сх-ся равн на [a,b], S(x) – его сумма. Для люб сущ первообр на [a,b]. Тогда S(x) также имеет первообр на [a,b].
14 |
Почленное интегрирование ФР и ФП. Сходимость в среднем, связь с равномерной сходимостью. |
Т. Если ФП
сх-ся на [a,b]
равн, каждая
интегр. на [a,b],
то и пред ф-ция интегр на [a,b],
причем ![]() .
Д-во.
.
Д-во.
1. Интегр f(x).
Она огр, т.к. ![]() Фиксируем
интегр. => можно выбрать разбиение:
Фиксируем
интегр. => можно выбрать разбиение: ![]() => Д-ем, что для нашего
=> Д-ем, что для нашего ![]() найдется n: что для любого
разбиения
найдется n: что для любого
разбиения ![]() (т.е.
(т.е. ![]() ).
Рассмотрим произв. разбиение [a,b],
обозначим
).
Рассмотрим произв. разбиение [a,b],
обозначим ![]() колебание на к-м частичном сегменте
колебание на к-м частичном сегменте ![]() и
и ![]() – колебание f(x).Неравенство
будет доказано, если
– колебание f(x).Неравенство
будет доказано, если ![]()
![]()
В силу равн. сх-ти для нашего
найдется n такой, что ![]()
Отсюда ![]() ;
; ![]() Построим две посл.,
Построим две посл., ![]()
Переходим к пределу, ![]() => Интегрируемость доказана.
=> Интегрируемость доказана.
2. Докажем, что ![]()
![]()
Доказательство завершено. Можно переформулировать в терминах функц. рядов.
Пусть каждая
и f(x) будeт интегр, тогда
![]() тоже интегрируема. ФП сх-ся на [a,b]
в среднем к f(x)
если существ. нулевой предел
тоже интегрируема. ФП сх-ся на [a,b]
в среднем к f(x)
если существ. нулевой предел ![]()
ФР сх-ся в среднем на [a,b]к сумме S(x), если посл част сумм сх-ся в среднем к пред. функции S(x).
Утв.1 Если
cходится к f(x)
равномерно на [a,b],
то эта послед. сходится к f(x)
и в среднем на [a,b].
Д-во. ![]() .
Отсюда
.
Отсюда ![]() .
Это и означает сходимость в среднем.
.
Это и означает сходимость в среднем.
Утв.2 Сходимость в среднем не влечет
ни равномерной, ни обычной сходимости
хотя бы в одной точке. Рассм посл сегментов
![]() .
.
![]() .
.
Утв.3 Cх-ть к f(x) на [a,b] не влечет сх-ти в среднем. Д-во. fn(x)=ne-nx, x из (0,1], 0, x=0.
Т.Если последовательность
сходится в среднем к f(x)
на [a,b], то
эту последовательность можно почленно
интегрировать на [a,b],
т.е. ![]() существует и равен
существует и равен![]() .Д-во.
.Д-во.
![]()
![]() ,
,
![]() .
.
![]()
![]() .
.
Можно переформулировать для ФР.
Утв.4 Cх-ть к f(x) на [a,b] не влечет возм почл интегр. Д-во. fn(x)=n2e-nx, x из (0,1], 0, x=0.
Утв.5 Возм почл интегр не влечет сх-ти в среднем. Д-во. fn(x)=n3/4e-nx, x из (0,1], 0, x=0.
Утв.6 Возм почл интегр не влечет сх-ти и равн сх-ти на [a,b]. Д-во. см утв. 2
15 |
Теорема Арцела. Пр равностепенной непрерывности ФП. |
Последоват. наз-ся равностепенно
непрерывной на {x}, если
![]()
![]() .
Пр. fn(x)=(-1)nx на R.
.
Пр. fn(x)=(-1)nx на R.
Т. (Арцела). Если ФП ![]() равностепенно непр. и равн огр на [a,b],
то из этой ФП можно выделить подпослед,
равн сх-ся на [a,b].
Д-во. Построим посл точек на [a,b].
x1 делит этот отрезок
надвое, вместе с х2 и х3 – на 4 части и т.
д., т. е. каждый раз разбиваем отрезки
надвое.
равностепенно непр. и равн огр на [a,b],
то из этой ФП можно выделить подпослед,
равн сх-ся на [a,b].
Д-во. Построим посл точек на [a,b].
x1 делит этот отрезок
надвое, вместе с х2 и х3 – на 4 части и т.
д., т. е. каждый раз разбиваем отрезки
надвое. ![]()
В точке ![]() выделим сходящуюся последовательность
выделим сходящуюся последовательность
![]()
Далее из этой последовательности выделим
сходящуюся подпослед. в точке ![]() .
.
И так далее. Теперь построим диагональную
послед. ![]() .
.
Т. к. послед. равностепенно непрерывна,
![]() Разобьем сегмент [a,b]
на конечное число отрезков меньше
Разобьем сегмент [a,b]
на конечное число отрезков меньше ![]() .
Из последовательности
.
Из последовательности ![]() Очевидно, диагональная последовательность
сходится в любой из этих точек. Поэтому
Очевидно, диагональная последовательность
сходится в любой из этих точек. Поэтому
![]() (критерий Коши).
(критерий Коши).
![]() |+|
|+|![]() |+|
|+|![]() (Критерий Коши), чтд.
(Критерий Коши), чтд.
Утв. 1 Пусть ФП {fn(x)} состоит из дифф-мых на [a,b] ф-ций и {fn'(x)} явл равн огр на [a,b] => {fn(x)} явл равност непр на [a,b]. Пр. fn(x)=sin2nx/n. Д-во. равн огр => сущ М>0: |fn'(x)|<=M люб n,x. люб x', x": |fn(x')-fn(x")|={т Лагранжа}=|fn'(φ)(x'-x")|<=M|x'-x"|<ε (δ=ε/M).
Утв. 2 Пусть {fn(x)} равност непр на [a,b] и сущ х0 из [a,b]: {fn(x0)} огр, тогда {fn(x)} равн огр на [a,b]. Д-во. сущ М>0: |fn'(x0)|<=M люб n. Равн непр => определение для ε=1. Разбиваем [a,b] на конечное число р отрезков длины <δ => колебание fn(x) люб n на [a,b] < p. Люб x из [a,b] <>x0: |fn(x)|<=|fn(x)-fn(x0)|+|fn(x0)|<p+M люб n.
16 |
Степенные ряды. Теорема Коши-Амадара. Непр-ть, дифф-ть, интегр-ть. Разложение ф-ций в степ ряды. |
![]() -
степенной ряд. Будем рассматр
-
степенной ряд. Будем рассматр
![]() .
Все сх-ся в х=0.
.
Все сх-ся в х=0.
Теорема Коши-Амадара. Рассмотрим степенной ряд.
1. Если последовательность ![]() не ограничена, то степенной ряд сходится
лишь при х=0. 2. Если последовательность
ограничена и имеет верхний предел L>0,
то ряд абсолютно сходится для значений
|x|<1/L и
расходится для |x|>1/L.
3. Если посл ограничена, и ее верхний
предел L=0, то ряд абсолютно
сходится для всех х. Д-во. 1. Если
послед. не ограничена, то для степенного
ряда нарушено необходимое условие
сходимости (члены не стремятся к нулю).
2. а) Фикс люб х: |x|<1/L.
Найдется
не ограничена, то степенной ряд сходится
лишь при х=0. 2. Если последовательность
ограничена и имеет верхний предел L>0,
то ряд абсолютно сходится для значений
|x|<1/L и
расходится для |x|>1/L.
3. Если посл ограничена, и ее верхний
предел L=0, то ряд абсолютно
сходится для всех х. Д-во. 1. Если
послед. не ограничена, то для степенного
ряда нарушено необходимое условие
сходимости (члены не стремятся к нулю).
2. а) Фикс люб х: |x|<1/L.
Найдется ![]() В силу свойства верхнего предела все
элементы
В силу свойства верхнего предела все
элементы ![]() начиная с некоторого номера. С этого
номера
начиная с некоторого номера. С этого
номера ![]() Сх-ся по признаку Коши. б) Фикс люб
|x|>1/L.
|x|>1/(L-
).
Можно выделить подпосл, сх-ся к L.
C некоторого номера
справедливо
Сх-ся по признаку Коши. б) Фикс люб
|x|>1/L.
|x|>1/(L-
).
Можно выделить подпосл, сх-ся к L.
C некоторого номера
справедливо ![]() Нарушено необходимое условие сходимости.
3. L=0, следоват. посл.
б/м. С некоторого номера
Нарушено необходимое условие сходимости.
3. L=0, следоват. посл.
б/м. С некоторого номера ![]()
![]() =>
сх-ся по признаку Коши.
=>
сх-ся по признаку Коши.
Т. Если степ ряд сх-ся не только в 0, то сущ число R>0: ряд сх-ся абс при |x|<R и расх |x|>R. R – радиус сх-ти. (-R,R) – интервал сх-ти. R=1/L. L=0 => сх-ть на всей числовой прямой. В x=+-R ряд может как сх-ся так и расх. Пр. xk, xk/k2, xk/k.
Лемма. Для люб r из (0,R) ряд сх-ся равн на [-r,r]. Д-во. х из [-r,r] => |akxk|<|ak|rk – сх-ся => по Вейерштр.
Сл. В усл леммы S(x) явл непр ф-цией внутри интервала сх-ти ряда.
Т. Сумма степ ряда внутри его инт сх-ти – непр ф-ция. Д-во. люб x из (-R,R) сущ r из (0,R): |x|<r => сл.
Т. R>0. Фикс люб х из (0,R) => степ ряд
можно почл интегр на [0,x], получ при этом
степ ряд имеет тот же радиус сх-ти
(аналогично для (-R,0) => люб [a,b]
из (-R,R)).
Д-во. сущ r из (0,R): 0<x<r<R,
на [-r,r] мжно почл интегр => и на [-x,x].
После почл интегр по [0,x] получим ряд
![]() - R1:
- R1:
![]() .
.
Т. R>0. Сумма степ ряда
– непр дифф-мая ф-ция, ряд можно дифф-вать
почл, получ при этом степ ряд имеет тот
же R. Д-во. Дост д-ть, что R при дифф-нии
не измен. Дифф-ем =>
![]() -
R1:
-
R1:
![]() .
.
Опр. f(x) может быть разложена в степ ряд на {x}, если найдется степ ряд, сх-ся к f(x) на {x}.
Утв. Если f(x) мб разложена в степ ряд на (-R,R), то она имеет непр произв люб порядка на (-R,R). Этот ряд – ряд Тейлора f(x), т.е. an=f(n)(0)/n!. Д-во. Вытекает из т о дифф-ти, записать f(n)(0).
Зам. Усл сущ произв люб порядка необх, но не дост для разлож-ти в ряд. Пр. f(x)=e-1/x^2, x<>0, 0, x=0.
Кр разлож-ти. f(x) мб разложена в степ ряд на {x} остаточный член в формуле Маклорена для f(x) →0 при n→∞ на {x}. Д-во. => люб x из {x}=> f(x)=Sn(x)+Rn+1(x) => Rn+1(x)→0 при n→∞. <= ф-ла Маклорена => f(x)=Sn(x)+Rn+1(x), Rn+1(x)→0 при n→∞ => |f(x)-Sn(x)|→0 люб x=> f разложима в ряд.
Пр.
![]() ,
,
![]() ,
люб х,
,
люб х,
![]() ,
х из (-1,1].
,
х из (-1,1].
17 |
Опр и д-во существования двойного интеграла. Классы интегр ф-ций. Основные св-ва двойного интеграла. |
Введение простейших определений: разбиения прямоугольника прямоугльниками, интегральной суммы, диаметра,верхней, нижней суммы, интегралов Дарбу. 7 утверждений про суммы.
Т. Для того, чтобы ограниченная на прямоугольнике R f(x,y) была интегрируема на R, необходимо и достаточно, чтобы для любого е>0 нашлось такое разбиение Т, для которого S-s<е.
Т. Любая непрерывная в прямоугольнике R f(x,y) интегрируема на R.
Опр. Назовём элементарной фигурой множество точек, являющихся объединением конечного числа прямоугольников, со сторонами, || осям координат.
Опр. Будем говорить, что функция f(x,y) обладает в прямоугольнике R (в произвольной замкнутой области D) I-свойством, если 1) f(x,y) ограничена в R (в D); 2) для любого е>0 найдётся элементарная фигура площади <е, содержащая все точки и линии разрыва f(x,y).
Т. Если f(x,y) обладает в прямогольнике I-свойством, то она интегрируема на нём.
Опр. Г назвают кривой площади 0, если для любого е>0 найдётся многоульгольник площади <е, содержащий в себе все точки Г.
Пусть D-замкнутая огр. область, граница Г которой имеет площадь 0, а f(x,y) определена в D и огр. R-прямоугольник со сторонами, || осям координат, содержащий D. Зададим F(x,y)=f(x,y) в D, и =0, если (x,y) в R\D.
Опр. f(x,y) назовём интегрируемой в D, если F(x,y) интегрируема в R. Назовём интеграл I f(x,y) по D= интегралу F(x,y) по R.
Утв. Интеграл f=1 по D=площади D, так как верхние инт суммы=площадям элементарных фигур, содержащих D, а нижние-содержащихся в D.
Т. Если f(x,y) обладает в D I-свойством, то она интегрируема в этой области.
F(x,y) обладает I-свойством в R, ибо она огр., а точки разрыва либо из f(x,y), либо с пересечения f c Г, но Г имеет площадь 0.
Сл1. Если f огр. в D и имеет в этой области разрывы лишь на конечном числе спрямляемых линий, то f интегрируема в D.
Сл2. Если f обладает I-свойством в D, а g огр. и совпадает с f всюду в D, за исключением мн-ва точек площади 0, то g инт., причём инт. g по D=инт. f по D.
Св-ва:
1.Аддитивность. Если f(x,y) инт. в D и если D кривой Г площади 0 разбивается на 2 связные и не имеющие общих внутренних точек области D1 и D2, то f инт. в каждой из этих областей, причем инт. по большой области равен сумме инт. по частичным областям.
2.Линейное св-во. Интегрируемость a*f(x,y)+b*g(x,y) и равенство этого интеграла а*инт(f)+b*инт(g)
3.Интегрируемость произведения f*g.
4.Если f<g, то и инт(f)<инт(g).
5.|инт(f)|<=инт(|f|), интегрируемость |f|.
6.Если f инт, а g совпадает с f всюду в D за исключением множества точек площади 0, то и g инт в D
7.Теорема о среднем значении.Если f и g инт в D, g знакопостоянна в D, M=sup(f), m=inf(f), то найдётся число µ: m<=µ<=M такое, что: инт(f*g)=µ*инт(g).
Если при этом f непрерывна в D, а D связана, то найдётся такая точка (a,b), что µ=f(a,b)
8.Геометрическое св-во. Инт от 1 по D=площади D.
18 |
Опред двойного интеграла при помощи произв разбиений обл. Эквивалентность двух определений. |
D-замкнутая огр. область с границей Г площади 0. Определение инт. суммы для разбиения этой области произвольными кривыми площади 0 на конечное число r замкнутых частитчых областей, каждая из которых квадрируема в силу того, что обладает границей площади 0.
Диаметр области-наибольшее расстояние между двумя точками области.
Определение предела инт. сумм при стремлении диаметра разбиения к 0.
Опр. (Общее опр. интегрируемости) f(x,y) называется интегрируемой в области D, если существует конечный предел инт. сумм. Этот предел называется двойным интегралом от f(x,y) по D.
Теорема. Общее опр. интегрируемости эквивалентно опр. при разбиении прямоугольниками.
1)Пусть f инт. в D согласно общему опр. и её двойной инт. согласно этому опр. =I. Заключим D в прямоугольник R, разобьём его на прямоугольники и ввёдем F=f на D и F=0 на R\D. Инт. суммы функции f согласно двум опр. могут различаться лишь слагаемыми, соответствующими частичным прямоугольным разбиениям, имеющим общие точки с границей Г области D. Поскольку Г имеет площадь 0, а f огр., то эта функция инт. и согласно опр. через прямоугольники. По этому же опр. она имеет инт=I.
2)Пусть теперь f инт.
согласно опр. разбиением прямоугольников
и I-двойной интеграл.
Докажем, что для f существует
равный I предел. Пусть S’
и s’ – верхняя и нижняя
суммы данного разбиения D.
S’= ![]() и s’=
и s’=![]() ,
где M’ и м’ – точные
верхняя и нижняя грань на соответствующих
частичных областях.
,
где M’ и м’ – точные
верхняя и нижняя грань на соответствующих
частичных областях.
Фиксируем произвольное е>0. Для него
найдётся разбиение Т прямоугольника Р
(D<Р) на частичные
прямоугольники Рк такое, что для
соответствующей F(x,y)
S-s<e/2
и ![]() ,
где Мо–точная верхняя грань |f(x,y)|.
,
где Мо–точная верхняя грань |f(x,y)|.
Заключим все отрезки прямых разбиения
Т и границу Г внутрь элементарной фигуры
Q, площадь которой<e/6Mo.
Тогда ![]() точная
нижняя грань
точная
нижняя грань ![]() расттояния между точками, принадлежащими
Q и точками разбиения или
границы. Пусть
расттояния между точками, принадлежащими
Q и точками разбиения или
границы. Пусть ![]() ,
тогда:
,
тогда:
Удалим из S’ все слагаемые
M’i![]() Di,
соответствующие областям Di,
каждая из которых не лежит целиком в
одном в одном частичном прямоугольнике
разбиения Т. Все такие области Di<Q,
так как di<=
Di,
соответствующие областям Di,
каждая из которых не лежит целиком в
одном в одном частичном прямоугольнике
разбиения Т. Все такие области Di<Q,
так как di<=![]() ,
а потому общая сумма таких площадей
<e/6Mo.
Получаем S’<
,
а потому общая сумма таких площадей
<e/6Mo.
Получаем S’<![]() +e/6,
где ‘ у суммы означает, что суммирование
распространяется лишь на области Di,
целиком лежащие в частичном прямоугольнике.
Теперь заменим M’i
на Mк-точные верхние грани
в прямоугольнике Рк и обозначим Рк’=
+e/6,
где ‘ у суммы означает, что суммирование
распространяется лишь на области Di,
целиком лежащие в частичном прямоугольнике.
Теперь заменим M’i
на Mк-точные верхние грани
в прямоугольнике Рк и обозначим Рк’=![]() Di,
где Di<Pк,
тогда получим S’<
Di,
где Di<Pк,
тогда получим S’<![]() +е/6.
+е/6.
Для Rк<D
области Rк\Rк’<Q,
поэтому для них ![]() <=
Q<e/6Мо.
<=
Q<e/6Мо.
Для прямоугольников, пересекающихся с
Г: ![]() <=
<=![]() е/6Мо.
е/6Мо.
Итого: |S-![]() =|
=|![]() )|<e/6+e/6=e/3,
т.е.
<S+e/3.
)|<e/6+e/6=e/3,
т.е.
<S+e/3.
Получаем S’<S+e/3+e/6=S+e/2.
Аналогично доказываем s-e/2<s’. Итого s-e/2<s’<=S’<S+e/2, а так как s и S отклоняются от I не больше, чем на е/2,то интегральная сумма сходится к I.
19 |
Сведение двойного интеграла к повторному однократному. |
Теорема. Пусть f(x,y)
интегрируема в прямоугольнике
R[a<=x<=b]*[c<=y<=d],
и для каждого a<=x<=b
существует I(x)=![]() ,
тогда существует
,
тогда существует ![]() .
.
Разобьём R точками {xk},{yl} на np частичных прямоугольников Rkl=[xk-1<=x<=xk]*[yl-1<=y<=yl] так, что х0=а, хn=b, y0=c, yp=d, xk>0, yl>0.
-диаметр разбиения прямоугольника R, Mkl-супремум f на Rkl, mkl, соответственно, инфинум, S и s-верхняя и нижняя суммы f. Тогда всюда на Rkl: mkl<=f(x,y)<=Mkl.
Фиксируем еk: xk-1<=ek<=xk
и положив в вышенаписанном неравенстве
x=ek и
проинтегривав его по y
получим: mkl
yl<=![]() <=Mkl
yl.
Просуммировав по l от 1 до
p и по k от
1 до n, умножив на
xk,
получим s=
<=Mkl
yl.
Просуммировав по l от 1 до
p и по k от
1 до n, умножив на
xk,
получим s=![]()
Устремим
к 0, тогда S и s
стремятся к ![]() ,
следовательно, средний член стремится
к тому же интегралу.Но этот предел по
опр однократного интеграла=
,
следовательно, средний член стремится
к тому же интегралу.Но этот предел по
опр однократного интеграла=![]() .
.
Теорема.Пусть выполнены следующие
условия: 1) область D такова,
что любая прямая, || Oy,
пересекает границу Г по целому отрезку
[y1(x);y2(x)],
либо не более, чем в двух точках, ординаты
которых y1(x)<=y2(x)
2) f(x,y)
интегрируема в D и для
любого x: x1<=x<=x2
допускает существование однократного
интеграла ![]() ,
где [x1;x2] –
проекция D на Ox.
Тогда существует
,
где [x1;x2] –
проекция D на Ox.
Тогда существует ![]()
Пусть R-прямоугольник со сторонами, || осям координат, содержащий D, а F(x,y)=f(x,y), если (x,y) принадлежит D и =0, если R\D. Для F выполнены все условия предыдущей теоремы, а значит, формула из неё переходит в необходимую (с учётом выбора F).
20 |
Кратные несобственные интегралы от неотрицательных функций. Признаки сходимости. |
D – открытое связное
множество пр-ва ![]() .
.
![]() – замыкание D (получено
присоединением к D его
границы).
– замыкание D (получено
присоединением к D его
границы).
Опр Пос-ть ![]() открытых связных мн-в монотонно
исчерпывает множество D,
если
открытых связных мн-в монотонно
исчерпывает множество D,
если
1) ![]() - включается в
- включается в![]() ;
2)
;
2) ![]() .
.
Пусть f(x),
х = (![]() )
– задана на мн-ве D,
интегрируема на любом замкнутом
кубируемом подмн-ве D.
)
– задана на мн-ве D,
интегрируема на любом замкнутом
кубируемом подмн-ве D.
Рассматриваем все {![]() },
монотонно исчерпывающ. D
и такие что все
},
монотонно исчерпывающ. D
и такие что все ![]() – кубируемы.
– кубируемы.
Опр Если ![]() пос-ти
{
}
существует предел числовой пос-ти:
пос-ти
{
}
существует предел числовой пос-ти: ![]() и этот предел не зависит от выбора
пос-ти {
},
то этот предел наз-ся несобственным
интегралом ф-ии f(x).
и этот предел не зависит от выбора
пос-ти {
},
то этот предел наз-ся несобственным
интегралом ф-ии f(x).
Опр Если описанный выше предел существует, то интеграл называют сх-ся, и расх-ся иначе.
Теорема. Для сх-ти несобств. интеграла
от неотр. в обл-ти D ф-ии
f(x), необходимо
и достаточно чтобы пос-ть ![]() }
была ограничена хотя бы для одной
монотонно исчерпывающ. мн-во D
пос-ти {
}.
}
была ограничена хотя бы для одной
монотонно исчерпывающ. мн-во D
пос-ти {
}.
Док-во: Необх-ть: сх-ть несобств. интеграла по определению означает сх-ть пос-ти } для всех { } монотонно исчерпывающ. мн-во D, т.е. она ограничена для всех пос-тей{ }.
Дост-ть: Пос-ть
}
– ограничена и не убывает(т.к.
содерж-ся
в ![]() ,
значит она сх-ся к нек. числу I.
Докажем что для всех ост. {
}
она сх-ся к тому же числу. Берем произв
пос-ть, фиксируем у нее номер
,
значит она сх-ся к нек. числу I.
Докажем что для всех ост. {
}
она сх-ся к тому же числу. Берем произв
пос-ть, фиксируем у нее номер ![]() ,
смотрим область с этим номером. Поймем
что в пос-ти из условия найдется такой
номер
,
смотрим область с этим номером. Поймем
что в пос-ти из условия найдется такой
номер ![]() ,
что
,
что
![]() (русская
– произв, англ – из условия) содерж-ся
в
(русская
– произв, англ – из условия) содерж-ся
в ![]() .(иначе
для любого k можно указать
точку
.(иначе
для любого k можно указать
точку ![]() из
,
которая не
из
,
которая не ![]() .
Тогда в силу замкнутости и огр-ти D
из
можно выделить сх-ся к M
.
Тогда в силу замкнутости и огр-ти D
из
можно выделить сх-ся к M
![]() подпос-ть. Но M с нек. ок-тью
лежит в одном из
подпос-ть. Но M с нек. ок-тью
лежит в одном из ![]() (и
всех с большими номерами), а это
противоречит выбору точек
).
Т.е.
содерж-ся
в
,
а значит
(и
всех с большими номерами), а это
противоречит выбору точек
).
Т.е.
содерж-ся
в
,
а значит ![]() .
Значит
.
Значит ![]() сх-ся к числу
сх-ся к числу ![]() .
Меняем в рассужд. Пос-ти местами и
получаем что к
.
Меняем в рассужд. Пос-ти местами и
получаем что к ![]() ,
т.е. сх-ся к
,
т.е. сх-ся к ![]() .
.
Теорема (общий признак сравнения).
Если на открытом мн-ве D
верно ![]() f(x)
f(x)
![]() g(x),
то из сх-ти несобств. интеграла ф-ии g(x)
след сх-ть для f(x),
и с расходимостью наоборот.
g(x),
то из сх-ти несобств. интеграла ф-ии g(x)
след сх-ть для f(x),
и с расходимостью наоборот.
Док-во Для пос-ти
верно: ![]() ,
т.е. из огр.
,
т.е. из огр. ![]() следует огр-ть
следует огр-ть![]() ,
а из неогр-ти
,
она же для
.
Т.е. признак верен в силу пред теоремы.
,
а из неогр-ти
,
она же для
.
Т.е. признак верен в силу пред теоремы.
21 |
Кратные несобств интегралы от знакоперем ф-ций. Эквивалентность понятий сх-ти и абс сх-ти. |
Опр Несобств интеграл ![]() сх-ся абсолютно, если сх-ся интеграл
сх-ся абсолютно, если сх-ся интеграл
![]() .
.
Теорема. Для m-кратных (m>1) интегралов понятия сх-ти и абс. сх-ти эквивалентны.
Док-во [из абс. обычная ] ![]() и
и ![]() ;
;
![]() ;
;
![]() из интегрир-ти f(x)
в любой кубир-й подобл-ти D
следует интегр-ть модуля, а значит и
из интегрир-ти f(x)
в любой кубир-й подобл-ти D
следует интегр-ть модуля, а значит и ![]() и
и ![]() (в силу из определения). Из сх-ти ряда из
модулей при помощи общего признака
сравниния(пред. билет) убеждаемся в
сх-ти
и
.
Из опред. из сх-ти несобств
и
следует сх-ть их разности, т.е.
.
(в силу из определения). Из сх-ти ряда из
модулей при помощи общего признака
сравниния(пред. билет) убеждаемся в
сх-ти
и
.
Из опред. из сх-ти несобств
и
следует сх-ть их разности, т.е.
.
[из обычной – абс.]Пусть
сходится, но не сх-ся абс. Т.е. пос-ть ![]() будет монотонн. возр. б.б. пос-тью. Значит
{
}
можно выбрать так, чтобы
будет монотонн. возр. б.б. пос-тью. Значит
{
}
можно выбрать так, чтобы ![]() (просто выбрасывая пром. члены не удовл
нер-ву.). обозначим
(просто выбрасывая пром. члены не удовл
нер-ву.). обозначим ![]() мн-во
мн-во
![]() .
Тогда
.
Тогда
![]() =
= ![]() >
> ![]() ,
т.е. больший из интегралов
или
(далее считаем что +)
,
т.е. больший из интегралов
или
(далее считаем что +) ![]() >
> ![]() .
.
Составим нижнюю сумму s
для нек. конечного разбиения обл-ти
(на
![]() частей) так, чтобы |s -
|< 1 (такая есть по лемме Дарбу) тогда s
частей) так, чтобы |s -
|< 1 (такая есть по лемме Дарбу) тогда s
![]() т.е.
т.е. ![]() .
По опр.
.
По опр. ![]() (
(![]() – нижняя грань области
– нижняя грань области![]() ,
,
![]() – ее m-мерный объем).
Выкинем из
– ее m-мерный объем).
Выкинем из ![]() области для которых
= 0; обозначим что осталось за
области для которых
= 0; обозначим что осталось за ![]() .
Т.к. в
ф-ия
.
Т.к. в
ф-ия ![]() > 0, то она совпадает с
> 0, то она совпадает с ![]() и сумму s можно заменить
на:
и сумму s можно заменить
на: ![]() .
Сложим с
.
Сложим с ![]() ,
получим при фикс n :
,
получим при фикс n : ![]() ,
где
,
где ![]() .
(в случае если вместо
было бы
было б < – n – 1). Тогда
для всех n
.
(в случае если вместо
было бы
было б < – n – 1). Тогда
для всех n ![]() .
.
Все бы хорошо, но ![]() может не быть связной. МАЛОЙ ДЕФОРМАЦИЕЙ
СДЕЛАЕМ ЭТИ ОБЛАСТИ СВЯЗНЫМИ. Дополним
каналами (кубируемые связные обл-ти из
изначального
может не быть связной. МАЛОЙ ДЕФОРМАЦИЕЙ
СДЕЛАЕМ ЭТИ ОБЛАСТИ СВЯЗНЫМИ. Дополним
каналами (кубируемые связные обл-ти из
изначального ![]() ,
которые соединят с обл-ми
,
которые соединят с обл-ми ![]() )
до связной обл-ти. Т.к. разбиение
- конечное, то и кол-во каналов конечно.
Обозначим объединение всех каналов
)
до связной обл-ти. Т.к. разбиение
- конечное, то и кол-во каналов конечно.
Обозначим объединение всех каналов
![]() .т.к.
f(x)
интегрируема, а значит ограничена на
,
то
.т.к.
f(x)
интегрируема, а значит ограничена на
,
то ![]() ,
где M = sup|f(x)|.
Потребуем чтобы m-мерный
объем каналов
,
где M = sup|f(x)|.
Потребуем чтобы m-мерный
объем каналов ![]() был < 1/M. Тогда
был < 1/M. Тогда ![]() и значит
и значит ![]() .
.
Т.е. пос-ть связных кубируемых областей
![]() (т.к.
(т.к. ![]() - включается в
- включается в![]() и
вообще говоря может совпадать с ним
берем четные номера) монотонно исчерпывает
область D, и пос-ть интегралов расх-ся,
т.е. несобст интеграл
расходится, но по усл-ю он сх-ся.
Противоречие и доказывает теорему.
и
вообще говоря может совпадать с ним
берем четные номера) монотонно исчерпывает
область D, и пос-ть интегралов расх-ся,
т.е. несобст интеграл
расходится, но по усл-ю он сх-ся.
Противоречие и доказывает теорему.
22 |
Криволинейные инт-лы первого и второго рода. |
Спрямляемая кривая L=AB,
не имеющ точек самопересеч и участков
самоналегания x=φ(t),y=ψ(t)=>
на ней опр f(x,y,),
P(x,y),
Q(x,y)
– вдоль L непр => равн непр. Разобьем
[a,b] на n част сегментов [tk-1,tk] => L на n
част дуг Mk-1Mk => Nk(ζk,ηk)=N(τk).
![]() .
Диаметр разбиения Δ=maxΔlk.
σ1=∑f(ζk,ηk)Δlk,
σ2=∑P(ζk,ηk)Δxk,
σ3=∑Q(ζk,ηk)Δyk.
.
Диаметр разбиения Δ=maxΔlk.
σ1=∑f(ζk,ηk)Δlk,
σ2=∑P(ζk,ηk)Δxk,
σ3=∑Q(ζk,ηk)Δyk.
Опр. I – предел интегр суммы σs при Δ→0, если люб ε>0 сущ δ>0: независимо от выбора Nk |σs-I|<ε, Δ<δ
Опр. Если сущ limσ1
при Δ→0, то это криволин
интегр первого рода от f(x,y) по L:
![]() .
.
Опр. Если сущ limσ2
(σ3) при Δ→0, то это
криволин интегр 2 рода от P(x,y) (Q)
по L:
![]() .
.
![]() - общий криволин интегр 2 рода.
- общий криволин интегр 2 рода.
