Ортонормированный базис

Биортогональный . У о\н базиса биортогональный совпадает с ним же.

Две пары биортогональных базисов. . (Здесь и далее 1 это штрих).

Матрицы

(2) Матрицы

Докажем, что

Возьмем , матрицы равны.

Линейный оператор .

Дивергенция =(rⁱ,Ar_i).

Т. Дивергенция инвариантна относительно выбора базиса. Д-во.

, за новый базис {rⁱ,r_i} => (r_i,Arⁱ)=(rⁱ,Ar_i).

Ротор

Т. Ротор инвариантен относительно выбора базиса. С точностью до квадратных скобок смотри пред. док-во.

27	Дивергенция, ротор и производная по направлению векторного поля. Повторные операции теории поля.

Опр. Векторное поле называется дифференцируемым в т. М, если приращение вект. поля Поле наз-ся диф. в области, если оно диф. в любой точке. Это представление единственно.

Перейдем к пределу, получится

Дивергенцией векторного поля наз-ся дивергенция оператора А из опр-я диф-сти.

Ротором векторного поля наз-ся ротор оператора А из опр-я диф-сти.

Пусть . Тогда производной по направлению назовем .

Утв. Если векторное поле дифференцируемо, то , где А из условия диф-ти. Д-во.

Пусть . Переходим к пределу, и получаем нужное рав-во.

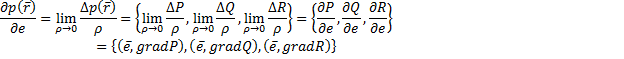
Найдем матрицу А в о\н базисе.

+ +

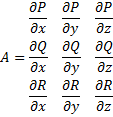
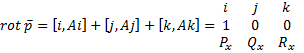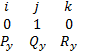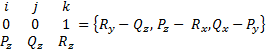
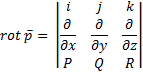
Повторные операции теории поля. Пусть дважды дифферен в D.

Все три операции можно применить повторно. 5 штук

28	Формула Грина. Формула Остроградского Гаусса.

Пусть π - пл-ть в , k – ед. в-р нормали к π, D – односвязная область на π(если любая кусочно гладкая замкнутая без самопересечений кривая, расположенная в D, огр обл., все точки кот. также принадл. D)

Пусть D уд. усл.:1)С -граница D – замкнутая гладкая без особых точек; 2)на π Oxy, что прямая II осям пересекает С не более, чем в 2 точках.

Пусть t - ед. в-р касательной к С, согласованный с k(напр t совпадает с напр полож обхода контура С)

Теорема. (формула Грина) Пусть a – вект. поле дифф-е в обл D, уд. условиям 1),2). а – такое, что его производная по любому направлению непрерывна в D C= . Тогда вып.:

(ф.Грина в инв форме выбора базиса) (1)

л.ч. - поток вихря rot а через D;

пр.ч. – циркуляция в.п. а по кривой С (работа сил поля а по перемещ точки вдоль С)

Док-во:т.к ф-ции из формул непрерывны, то интегралы из формулы существуют. Все велечины в (1) инв отн выбора базиса, тогда докажем в спец. выбранной системе Oxyz: Oxy выбираем в π, так чтобы вып 2), а Oz вдоль k. В.п. а=P(x,y)i+ Q(x,y)j+R(x,y)k – плоско, то R=0, t={cosα, cosβ, 0}={cosα, sinα, 0}. Тогда rot а =( )k. Далее: (k,rot а ) = ; (a,t)=Pcosα + Qsinα

т.к для пл-ой обл dσ=dxdy, то и = (тк dx=cosαdl и dy=sinαdl, l – длина дуги С, параметр, возр кот согласовано с напр обхода С)

Докажем теперь, что I= - = и J= =

Для этого построим рис, где прямая х пересекает С в двух точках (x,y (x)) и (x,y (x)), где y (x) y (x).

пусть x и x - наим и наиб абсциссы , пересекают соотв в т А и В(С1 соединяет А с В, С2 соед В с А) С=С1 С2(ориент согласовано с С), тогда по формуле сведения дв инт к повторному получаем все ок=)

(там пределы первого инт от x до x , а второго от y (x) до y (x)))

Замечание1 можно избавиться в теореме от усл 2), но док усложняется

Замечание2 верна и для С – спрямляемой кривой

Замечание3 дост требовать: непр а в , дифф в D и непр произв по напр только в D, тогда двойн инт в формуле следует понимать как несобственный

Замечание4 верна и для D таких, что D= D , для D вып 1) и 2)

Пусть D – односвязная обл-ть в , S – ее граница уд усл:

1)S –кусочн гладк 2-сторонн полн ограниченная замкнутая пов-ть без особых точек;

2)в Oxyz, что прямая II осям пересекает S не более, чем в 2 точках.

n – единичный вектор нормали к S

Теорема(Формула Остроградского-Гаусса)Пусть a – вект. поле дифф-е в обл D, уд. условиям 1),2). а – такое, что его производная по любому направлению непрерывна в D C= . Тогда вып.: = (2)

Док-во:в принципе анолог только для тройного инт, т.е. выбираем Oxyz уд 2),; =

Док-ть для: I= = и для Q и R тоже

Для этого строим пов-ть S, затем ее проекц на Oxy , через граничные точки проекц проводим прямыеII Oz(каждая пересекают S в одной точке, тем самым делим S на две пов S1 и S2), проводим из внутр точки проекц еще одну прямую II Oz , она пересекает S вдвух точках (x,e,z1) и (x,y,z2). Теперь сводим тройной инт к повторному (дв инт по этой проекц, а второй одном инт от z1(x,y) до z2(x,y))

Замечание 1,2,3 анолог замечаниям 1,2,3 в Грине

29	Формула Стокса.

Опр. S – односвязная пов-ть, если любая кусочно гладкая кривая без точек самопересечения, расположенная на S, огр-ет мн-во, целиком сост-ее из точек этой пов-ти.

Опр. t - вектор, согласованный с n(нормаль к S, содержащ. контур С), если положит. направление обхода С в точке приложения t совп. с напр t, и если смотреть с конца нормали n то контур С ориентирован положит-но (его обход против часовой стрелки).

Пусть S – односвязная пов-ть в , удовл. условиям:

1) S –кусочн гладк 2-сторонн полн пов-ть без особых точек; замкн кусочн гладк контур С ее граница.

2) Есть декарт. система такая, что S однозначно проектир-ся на любую из трех коорд пл-тей.

n – единичный вектор нормали к S. t – единич. вект. касат-й к С, согласов-й с n.

Теорема. (формула Стокса) Пусть задано a – вект. поле дифф-е и имеющ. непр. производн. на нек. открытом мн-ве содерж S. Тогда справедлива формула: . (в др. формулировке – поток вектора rot a через пов-ть S равен циркуляции вектора а по замкн. конт. С).

Док-во Из усл. теоремы интегралы из формулы существуют. Формула инвар-на отн-но выбора базиса, значит выберем дек.систему коорд. где S однозначно проектир-ся на любую из трех коорд пл-тей и док для нее. Согласуем выбор сист. коорд. так, чтобы n имел острые углы с коорд. осями. Пусть , , . Т.к. , получим: ? . Док-м что , для прочих компонент будет аналогично.

Т.к. S – кусочно гладк однозначн проектир-я на Oxy, то существует диффер-я ф-ия , однозначно задающая S. 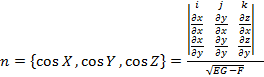При этом 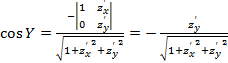. Аналогично . Тогда, если D – проекция S на Oxy, Г-ее граница, то

. (Последнее рав-во следует из того, что если точка ).

Зам 1. Ф-ла Стокса верна для пов-тей S, удовл усл-ю 1) и не удовл усл-ю 2)

Док-во Это следует из того, что для всех точек есть ок-ть с которой эта точка проектир-ся на все пл-ти. Осталось док-ать что есть универсальное есть (не зависящее от выбора точек), что делается от противного – строим пос-ть точек при , ок-ть размера меньше и не проецир-ся однозначно, выделим из этой сх-ся подпос-ть, и придем к противоречию с тем что ее предел однозначно проектир-ся на коорд пл-ти. Тогда разобьем на области размера < , их будет конечное число,(для них вып-на теорема). Просуммируем левые и правые части, интегралы по кривым разбиения будут браться в разные стороны, поэтому сократятся. И получим что надо.

Зам 2.Ф-ла Стокса верна и для пов-тей S, допускающ разбиение кусочн гладк кривыми на конеч число односвязн, обл. св-вом 1) пов-тей. Док-во Просуммируем все интегралы, интегралы по кривым разбиения будут браться в разные стороны, поэтому сократятся.

Зам 3. Ф-лу Стокса можно писать так(след из док-ва):

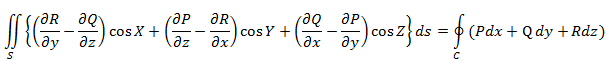
30	Условия независимости криволинейного интеграла 2 рода на пл-ти от пути интегрирования.

Теорема. Пусть D – связная обл-ть на Oxy. Ф-ии P(x,y) и Q(x,y) непрерывны на D. Тогда следующие утверждения эквивалентны:

1) , где L – кусочно гл-кий контур.

2) Значение не зависит от огранич. кусочно-гладк. кривой, соед А и В и целиком лежащ в D.

3) Существует ф-ия u(x,y) опред на D, такая что 1) 2) для любй огр кус-но гл-кой кривой, соед А и В и целиком лежащ в D.

Док-во Возьмем кривые АС₁В и АС₂В, тогда , значит .

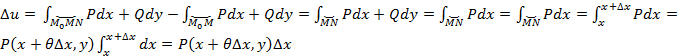Фиксируем произв точку М₀ из D. Пусть Док-м что u – подходит. Пусть даны т-ки М(x,y) и N . Т.е.

. т.е. , т.е. , аналогично .

.

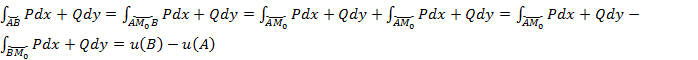Пусть L – кус. гладкая кривая из D. Тогда

Зам Любая кус-гладкая и огр кус гладкая кривая имеют не более чем конечн число точек самопересечения.

Теорема Пусть D – связная обл-ть на Oxy. Ф-ии P(x,y) и Q(x,y) непрерывны и дифф на D (сущ непр и ). Тогда следующее усл эквивалентно утв-ям пред теоремы:

4) = в обл-ти D

Док-во: для u верно , , значит в силу непр-ти = =

В силу односв-ти D, L огр-ет обл-ть D^* подобл-ть D. И верна ф-ла Грина в ОНБ: