63 Определенный интеграл как предел интегральных сумм.

Пусть функция у=ƒ(х) определена на отрезке [а; b], а < b. Выполним следующие действия.

1. С помощью точек х₀=а, x_1,х_2,
...,х_n= В (х₀ <x₁ < ...< х_n) разобьем отрезок [а, b] на n частичных отрезков [х₀;х₁], [x₁; х₂],..., [х_n-1,х_n] (см. рис. 167).

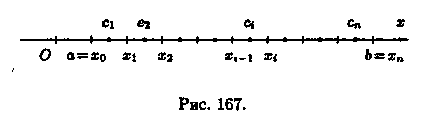
2. В каждом частичном отрезке [x_i-1;x_i], i = 1,2,...,n выберем произвольную точку с_i є [x_i-1; x_i] и вычислим значение функции в ней, т. е. величину ƒ(с_i).

3. Умножим найденное значение функции ƒ (с_i) на длину ∆x_i=x_i-x_i-1 соответствующего частичного отрезка: ƒ (с_i) • ∆х_i.

4. Составим сумму S_n всех таких произведений:

Сумма вида (35.1) называется интегральной суммой функции у = ƒ(х) на отрезке [а; b]. Обозначим через λ длину наибольшего частичного отрезка: λ = max ∆x_i(i = 1,2,..., n).

5. Найдем предел интегральной суммы (35.1), когда n → ∞ так, что λ→0.

Если при этом интегральная сумма S_n имеет предел I, который не зависит ни от способа разбиения отрезка [а; b] на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции у = ƒ(х) на отрезке [а; b] и обозначается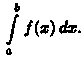Таким образом,

Числа а и b называются соответственна нижним и верхним пределами интегрирования, ƒ(х) — подынтегральной функцией, ƒ(х) dx — подынтегральным выражением, х — переменной интегрирования, отрезок [а; b] — областью (отрезком) интегрирования.

Функция у=ƒ(х), для которой на отрезке [а; b] существует определенный интеграл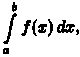называется интегрируемой на этом отрезке.

Сформулируем теперь теорему существования определенного интеграла.

Теорема 35.1 (Коши). Если функция у = ƒ(х) непрерывна на отрезке [а; b], то определенный интеграл

Отметим, что непрерывность функции является достаточным условием ее интегрируемости. Однако определенный интеграл может существовать и для некоторых разрывных функций, в частности для всякой ограниченной на отрезке функции, имеющей на нем конечное число точек разрыва.

Укажем некоторые свойства определенного интеграла, непосредственно вытекающие из его определения (35.2).

1. Определенный интеграл не зависим от обозначения переменной интегрирования:

Это следует из того, что интегральная сумма (35.1), а следовательно, и ее предел (35.2) не зависят от того, какой буквой обозначается аргумент данной функции.

2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю:

3. Для любого действительного числа с.

64 Производная определенного интеграла по верхнему пределу.

Если в определенном интеграле изменять верхний предел b, то будет меняться и значение интеграла, то есть интеграл будет функцией верхнего предела.

Обозначим верхний предел x, а переменную интегрирования, чтобы не смешивать ее с верхним пределом, обозначим t. Таким образом, интеграл с переменным верхним пределом является функцией от x: .

Имеет место теорема: производная интеграла с переменным верхним пределом от непрерывной функции равна подынтегральной функции, в которой переменная интегрирования заменена верхним пределом: