
- •В наведеному прикладі
- •Вірні значущі цифри.
- •Похибки суми та різниці
- •Похибка добутку
- •Похибки частки та число вірних знаків частки.
- •Похибки степеня та кореня.
- •Правила підрахування цифр.
- •Розрахунок похибок функцій багатьох змінних.
- •Визначення допустимої похибки аргументів по допустимій похибці функцій.
- •Точність представлення чисел в Комп'ютері
- •Форми представлення 2-их чисел в еоп
- •Похибки представлення чисел.
- •Стійкість, коректність та збіжність.
- •Числове інтегрування
- •Формула прямокутників
- •Формула трапеції
- •Формула сімпсона
- •Похибки
- •Теорема Больцано-Коші
- •Алгоритми відділення коренів рівняння
- •Алгоритми уточнення коренів.
- •1)Алгоритм уточнення кореня методом половинного ділення.
- •Програма методу перебору
- •Алгоритм уточнення кореня рівняння методом половинного ділення
- •Алгоритм уточнення кореня методом хорд
- •Mетод дотичних
- •Метод ітерацій (метод послідовних наближень)
- •Числові методи розв’язування систем лінійних рівнянь
- •Алгоритм
- •Алгоритм для системи нормального вигляду
- •Метод ітерації
- •Метод ітерацій Зейделя (ітерації)
- •Оптимізація
- •Алгоритми наближення функції
- •Інтерполяційний багаточлен Лангранжа
- •Коефіцієнти Лангранжа які задовільняють умовам:
- •Блок-схема алгоритму
- •Апромаксимація. Метод найменших квадратів
Mетод дотичних
Y
x0
x1
x2 F(a) A F(A) a F(B) F(b) B X x*
y-F(x0)=F’(x0)*(x1 –x0)
Точка перетину x1 відповідає у=0. Тому
x1-x0=-F(x0)/F’(x0);
Рекурентна формула - формула методу дотичних.

В якості початкового наближення x0 вибирається той кінець відрізку ізоляції, де виконується
F’(x0)*F’’(x0)>0
Комбінований
У X B A a
x1
x2
x1
x2 b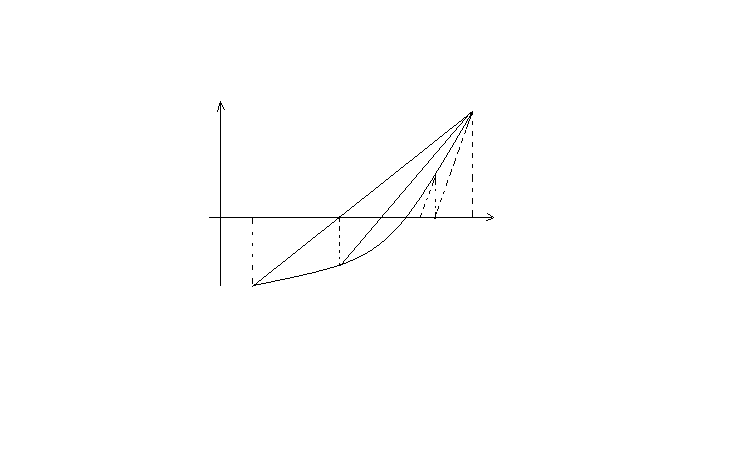


Метод ітерацій (метод послідовних наближень)
Для знаходження дійсних коренів рівняння F(x)=0, де F(x) неперервна на a,b, його замінюють на рівносильне рівняння
x=(x) (1)
Це можна зробити завжди, причому різними способами. Наприклад:
x3-9x+3=0
1 .x=![]()
2. x=![]()
3. x=x3-8x+3
4. 7x=x3-2x+3
Нехай відомий відрізок ізоляції кореня a,b. Тоді за початкове наближення шуканого кореня беруть
![]()
![]() (2)
(2)
Підставляємо x0 в праву частину (1) і знаходимо перше наближення
x1=(x0) (3)
x2=(x1) (4)
Рекурентна формула методу ітерацій:
xn+1=(xn) (5)
Вияснити, чи збігається ітераційна послідовність. Якщо збігається, то
xn*=![]()
якщо ні, то процес ітерацій треба замінити іншим.
Можна показати, що метод
ітерації можна застосовувати, якщо
![]() ,
де M1-
максимальне значення
,
де M1-
максимальне значення
![]() на
відрізку a,b
на
відрізку a,b
![]() (6)
(6)
Y X A B C y=x
y=(x)
x0
x1
x2
x0
x1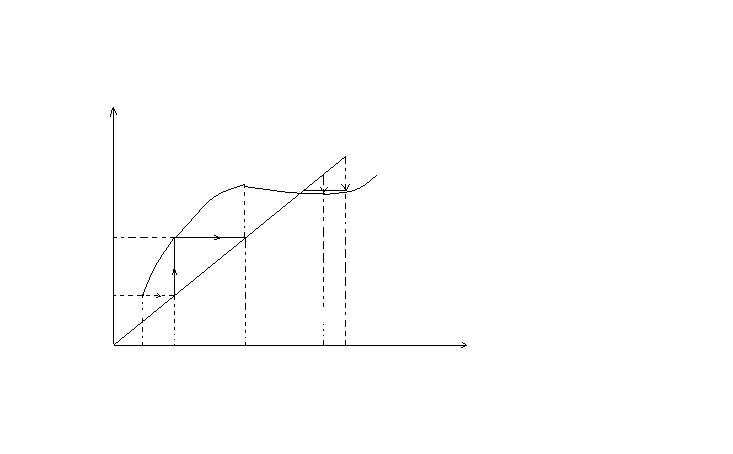
x=(x)-точка перетину
цих 2-х графіків є розв’язок
Числові методи розв’язування систем лінійних рівнянь
a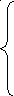 11x1
+ a12x2
+ …+ a1nxn
= b1
11x1
+ a12x2
+ …+ a1nxn
= b1
a21x1 + a22x2 + …+ a2nxn = b2
.
.
![]() aijxj=
bi (i
= 1,n)
aijxj=
bi (i
= 1,n)
.
an1x1 + an2x2 + …+ annxn = bn
Число елементарних операцій при розв’язуванні лінійних систем з n-змінними пропорційно n3.
Нехай система має єдиний розв’язок і число невідомих співпадає з кількістю рівнянь. За способом організації обчислень методи розв’язку систем лінійних рівнянь можна розділити на прямі та ітераційні.
Прямі методи дозволяють отримати розв’язок системи у вигляді точних формул після виконання скінченого числа арифметичних операцій над коефіцієнтами системи і вільними членами. Це метод Гауса і правило Крамера.
Ітераційні методи дозволяють отримати розв’язок системи з заданою точністю шляхом нескінченно збіжних процесів. Із наближених методів розглянемо метод ітерацій.
За способом організації обчислень методи розв’язку систем лінійних рівнянь можна розділити на прямі та ітераційні.
Прямі методи дозволяють знайти розв’язок у вигляді точних формул. Термін ,,точний’’ є характеристикою алгоритму обчислень, а не реального обчислювального процесу. Абсолютно точний результат неможливий через обмеженість розрядної сітки. Прямі методи мають переваги: заздалегідь відома точна кількість операцій, які потрібно виконати. Вони універсальні, але разом з тим мають недоліки:
-
Вимагають збереження в ОП всіх елементів матриці А, навіть, якщо серед них є багато нульових.
-
При розрахунках відбувається накопичення похибок, так як результат наступного кроку обчислень використовує результат попереднього.
-
При застосуванні прямих методів доцільно розв’язувати системи з густо заповненою матрицею. Тому широко використовують ітераційні методи. В них задається початкове значення невідомих: x1(0), x2(0),…,xn(0) і врезультаті ітераційних циклів отримуються наступні наближення. Вважається, що розв’язок знайдений з точністю , якщо виконується умова xi(n)-xi(n-1) (i=1,2,…,n) .
Переваги:
-
Ітераційні методи не завжди вимагають збереження всієї матриці. Потрібні коефіцієнти можна знаходити в процесі розрахунку.
-
Вони не накопичують похибок так як результат на n-ітерації не залежить від попередніх разів.
-
Вони годяться для широкого класу систем і погано обумовлених систем.
Вибір методу розв’язку систем лінійних рівнянь залежить від кількох факторів:
1.Від особливостей матриці А
2.Від розмірності А
3.Від характеристик комп’ютера: його швидкодії, ОП, зовнішніх носіїв.
AX=B
Матриця коефіцієнтів називається неособливою або не виродженою, якщо існує обернена до неї матриця А-1А= АА-1= І.
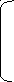
 a11
a12
. . . a1n
a11
a12
. . . a1n
.
A = .
.
an1 an2 . . . ann
X =
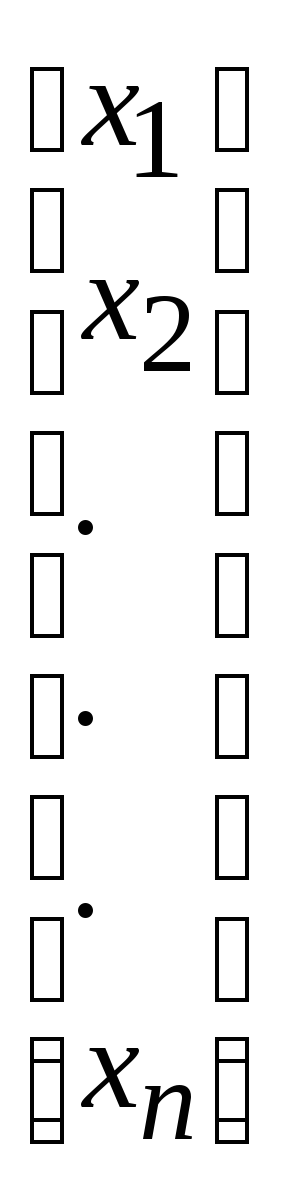 B =
B =
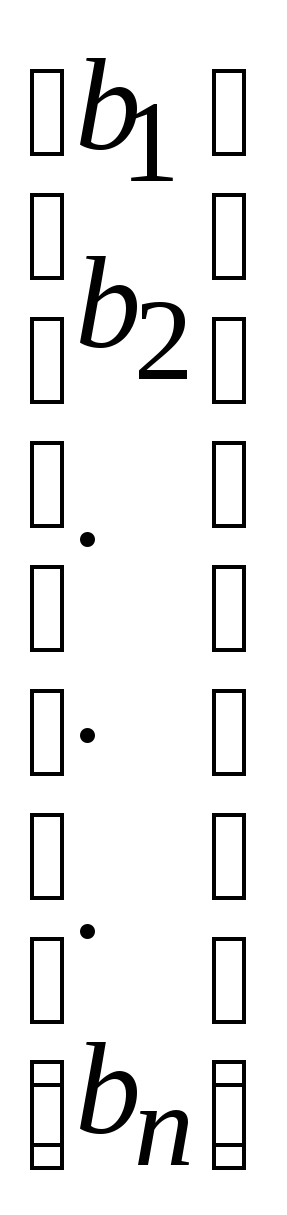
a 11
0 0 0
11
0 0 0
0 a22 0 0
0 0 a33 0 - діагональна квадратна
0 0 0 ann

1 0 0 0
0 1 0 0 - одинична, нульова
0 0 1 0
0 0 0 1
Якщо застосовувати до систем лінійних рівнянь елементарні перетворення, то отримаємо рівносильні системи, тобто системи, що мають такий же розв’язок. Елементарні перетворення:
-
множення всіх елементів рядка на одне і те ж число, яке 0.
-
додавання до елементів одного рядка відповідних елементів іншого рядка, помножених на загальне для всіх число.
-
перестановка рядків або стовпців.
Метод послідовного виключення змінних ( Гауса)
В ін
оснований якраз на елементарних
перетвореннях. Схема – квадратна матриця
перетворюється в трикутну. Розберем
схему єдиного ділення.
ін
оснований якраз на елементарних
перетвореннях. Схема – квадратна матриця
перетворюється в трикутну. Розберем
схему єдиного ділення.
a11х1 + а12х2 + а13х3 = b1
a21х1 + а22х2 + а23х3 = b2
a31х1 + а32х2 + а33х3 = b3
Нехай а11 0
Розділимо коефіцієнти першого
рівняння і вільний член на а11.
Отримаємо а![]() =
=
![]() і b
і b![]() =
=
![]() (1)
(1)
x1
+ a![]() x2
+ a
x2
+ a![]() x3
= b
x3
= b![]() (2)
(2)
Тепер виключимо змінну х2 з другого і третього рівнянь. Для цього від другого рівняння віднімемо перше, помножене на а21, а від третього - помножене на а31. Отримаємо
 a
a![]() x2
+ a
x2
+ a![]() x3
= b
x3
= b![]() (3)
(3)
a![]() x2
+ a
x2
+ a![]() x3
= b
x3
= b![]() , де
(4)
, де
(4)
a![]() = аij -
a
= аij -
a![]() ai1
(i = 2,3; j = 2,3)
ai1
(i = 2,3; j = 2,3)
b![]() = bi -
a
= bi -
a![]() b
b![]()
Далі (3) ділимо на а![]()
x2 + a![]() x3
= b
x3
= b![]() і
виключимо х2
із (4).
і
виключимо х2
із (4).
Отримаємо х3
=
![]()
Якщо х1, х2, х3 підставити в початкову систему, то повинні отримати тотожність, але в зв’язку з тим, що проводились заокруглення чисел, то в результаті підстановки отримаємо деякі числа, відмінні від нуля. Ці числа називають нев’язками. Якщо нев’язки малі, то рішення є вірним.
