Теорема Больцано-Коші

Якщо неперервна функція F(х) приймає значення різних знаків на кінцях відрізку [а;b]  X, тобто F(a)F(b) 0, то всередині цього відрізку міститься по крайній мірі один корінь рівняння F(x) = 0, тобто знайдеться хоча б одне число х*  ] а; b [ таке, що F(х*) = 0.

Надалі F’(х)  0

Теорема 2: Якщо функція F має першу похідну, яка не змінює знаку на відрізку [а;b], то при виконанні умов теореми 1, рівняння F(x) = 0 має на цьому відрізку єдиний корінь.

Алгоритми відділення коренів рівняння

Є 3 методи відділення коренів: аналітичний, графічний, перебирання.

а) Аналітичний метод:

1. Знайти область визначення рівняння – множину всіх значень аргумента, при яких визначені функції, що входять в рівняння.

2. Обчислити F’(x) і знайти критичні точки.

3. Записати інтервали монотонності.

4. Дослідити знак функції на кінцях інтервалів монотонності.

5. Виписати відрізки ізоляції коренів.

6. Отримані відрізки ізоляції коренів звузити яким-небудь методом.

F(x) = x³ – 4x² +2 = 0

1. X = ];[

2. F’(x) = 3x²-8x; 3x²-8x = 0;  критичні точки: 0; 8/3;

3. Інтервали монотонності ], 0[ ; ]0, 8/3[ ; ] 8/3, [

4. Дослідження знаку функції на кінцях інтервалів монотонності дає lim F(x) = -; F(0) = 2; F(8/3) = -202/27; lim F(-) = + 

5. Відрізки ізоляції коренів ] - , 0 [ ; ] 0, 8/3 [ ; ]8/3, +[ ;

6. Методом проб звузимо отримані інтервали

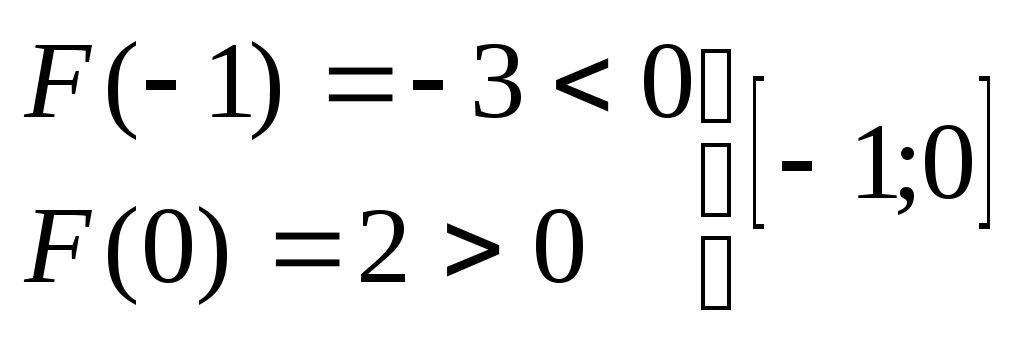
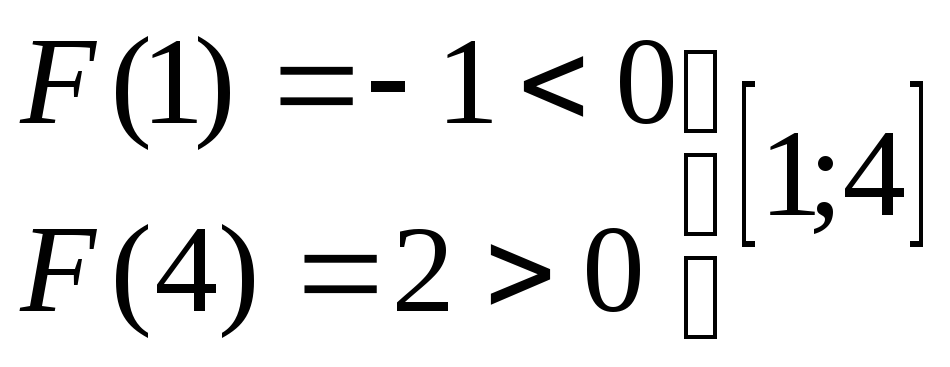
б) Графічний метод :

1. F(x) = 0;

2. F(x) = 0  f(x)=(x) і будуємо графіки функцій y₁=f(x) і у₂=(х). Абсциса точки перетину цих графіків буде коренем рівняння (1).

в) Алгоритм відділення коренів методом послідовного перебору

Велика продуктивність сучасних ЕОМ дає можливість відділити всі дійсні корені рівнянь крім кратних методом послідовного перебору.

Нижню границю А і верхню В коренів вибирають приблизно виходячи із фізичного змісту задачі, що описується рівнянням або із графіку у=F(x). В основі цього методу лежить теорема 1. Вибирається початкове значення х = А, потім з фіксованим кроком Δх = Н обчислюється значення функції F в точках А+ кН (к = 0,...) до тих пір поки вона не змінить знак. Нехай після n-ого кроку в точці х = А + nН функція змінила знак, тоді [А + (n-1)H; A + nH] - відрізок ізоляції кореня, а Р=А+nH – H/2 – наближене значення кореня рівняння з точністю ε = Н/2. Правий кінець цього відрізку

приймають за початкове значення наступного кореня, якщо він є.

Алгоритми уточнення коренів.

1)Алгоритм уточнення кореня методом половинного ділення.

Нехай яким-небудь методом знайдений відрізок ізоляції кореня [а;b] рівняння F(x) = 0, де F(x) неперервна на [а;b], і F(a)F(b) 0. Потрібно звузити цей відрізок так, щоб його довжина стала не більшою наперед заданої точності обчислення кореня, тобто |b - а|≤ε . Цей процес звуження інтервалу, що містить ізольований корінь, називається уточненням кореня. В цьому алгоритмі відрізок ізоляції кореня [а;b] ділять навпіл точкою Х = і обчислюють значення F(Х). Якщо F(Х) = 0, то Х – значення шуканого кореня рівняння і задача розв’язана. Якщо F(Х)  0 , то шуканий корінь знаходимо на одному із двох відрізків [а;Х] або [Х;b], на кінцях якого функція F приймає значення різних знаків. Позначимо цей відрізок через [а₁;b₁] , його довжина b₁ – a₁ = . З відрізком [а₁;b₁] чинять так само як із відрізком [а;b]. Цей процес послідовного ділення відрізка навпіл продовжують до тих пір, поки не буде одне із двох:

1. або знайдеться така точка Х_n = , в якій F(Х_n) = 0( що малоймовірно) і задача розв’язана;

2. або такої точки не знайдеться, але при деякому n прийдемо до відрізка [а_n;b_n] довжини b_n – a_n = ≤ε, що містить в собі шуканий корінь. Тоді числа а_n і b_n є наближеними значеннями шуканого кореня з недостачею і надлишком, відповідно.