Алгоритм для системи нормального вигляду

1. Привести до нормального вигляду.

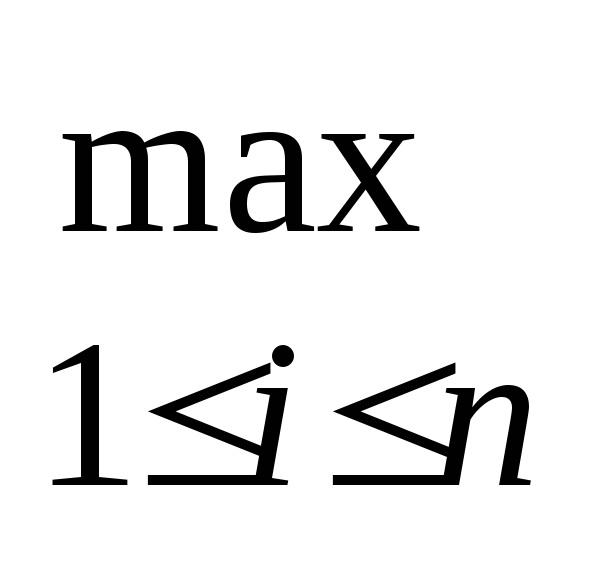
2. Обчислити q= ‌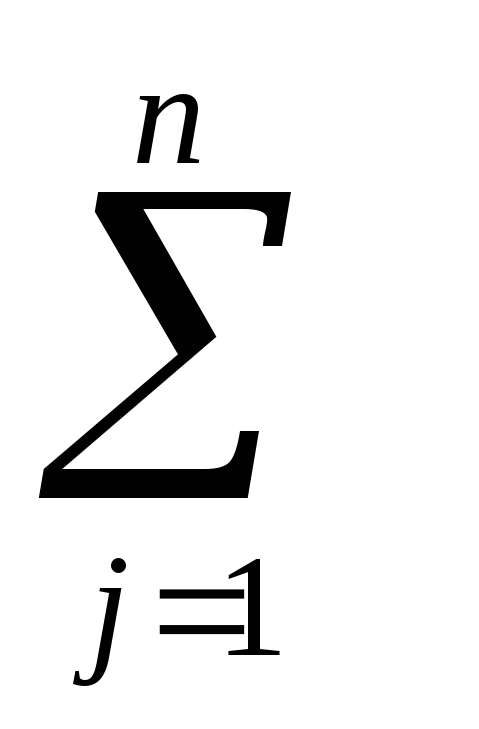|α_ij|.

3. Перевірити умову q<1. Якщо не виконується, то метод не можна застосовувати.

4. Визначити допустиму похибку ε₁=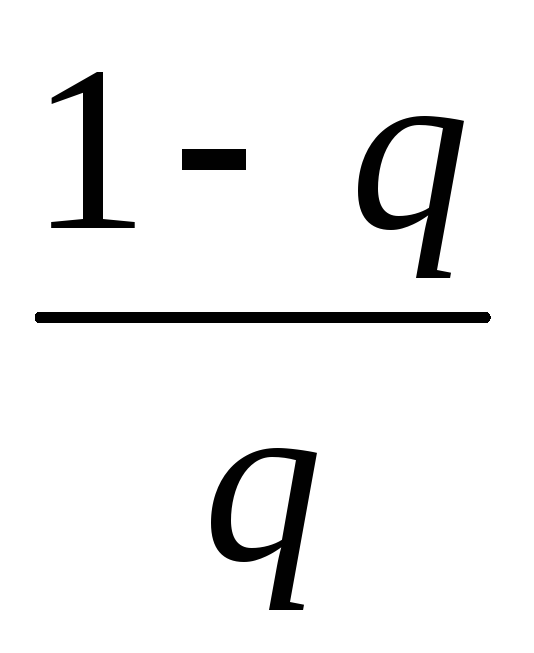•ε.

5. Вибрати початковий розв’язок x_i⁽⁰⁾ = β_i .

6. Обчислити нове наближення у_і, якщо відоме попереднє х_і.

7. Перевірити умову |у - x| < ε₁. Якщо виконується, то процес закінчити; якщо ні, то → 6.

Метод ітерації

N=5

DIM B(N), A(N,N), X(N),Y(N), P(N)

INPUT A,B,EPS

FOR I= 1 TO N

S=0

FOR j=1 TO N

S=S+ABS(A(i,j))

NEXT j

IF (S<1) THEN 10

PRINT (“Метод не застосовується”)

GOTO 30

10 P(I)=S ‘ P(I)=|α_ij| <1

NEXT i

Q=P(1)

FOR i=2 TO N

IF Q<=P(i) THEN Q=P(i)

NEXT i

EPS= (1-Q)*EPS/Q ‘ε₁=·ε

FOR I=1 TO N

X(i)=B(I)

NEXT i

9 H=0

FOR i=1 TO N

T=0

FOR j=1 TO N

T=T+A(i,j)*X(j)

NEXT j

Y(i)=T+B(i)

C=ABS(Y(i)-x(i))

IF C>H THEN H=C

NEXT i

FOR I=1 TO N

X(i)=Y(i)

NEXT i

IF H>=EPS1 THEN 9

PRINT(“Розв'язок”, X(i))

END

Метод ітерацій Зейделя (ітерації)

Метод ітерацій Зейделя відрізняється від методу ітерацій тільки одним : виразами для отримання невідомих на наступній ітерації, тобто

x[1]= 1-xo[2]+2xo[3]-3xo[4]

x[2]= 4+3x[1]-xo[3]-2xo[4]

x[3]= 6+2x[1]+3x[2]+xo[4]

x[4]= 4+x[1]+2x[2]+3x[3]

Приклад,

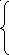x₁₊x₂+2x₃+3x₄=1 x₁=1-x₂-2x₃-3x₄

3x₁-x₂-x₃-2x₄=-4 ==> x₂=4-3x₁-x₃-2x₄

2x₁+3x₂-x₃-x₄=-6 x₃=6+2x₁+3x₂-x₄

x₁+2x₂+3x₃-x₄=-4 x₄=4+x₁+2x₂+3x₃

program ite 2

label mitka 1, mitka 2;

var

m, k max, i, j: integer;

x: array [1…4] of real;

x0: array [1…4] of real;

eps: real;

begin

write (‘eps=’); readln (eps); write(‘max=’); readln(max)

x0[1]:=1; x0[2]:=-4; x0[3]:=-6; x0[4]:=-4;

mitka 1: k:=0; k:=k+1;

x[1]:=1-x0[2]-2*x0[3]-3*x0[4];

x[2]:= ;

x[3]:= ;

x[4]:=4+x0[1]+2*x0[2]+3*x0[3];

m:=0;

for i:=1 to 4 do

if ABS(x[i]-x0[i])<eps then m:=m+1;

if m=4 then begin

for i:=1 to 4 do

write(‘x(‘,i,’)=’,x[i]);

write(‘eps=’,eps);

go to mitka 2;

end;

if k=max then begin

write(‘меод не збігається,k=’,k),

go to mitka 2;

end;

else begin

for 1:=1 to 4 do

x0[i]:=x[i];

go to mitka 1;

end;

mitka 2;

end.

Обчислення значень елементарних функцій.

1. Обчислення значень алгебраїчних багаточленів за схемою Горнера [2n-1 множень, n- додавань, а в схема - n- множень та n- додавань, на множення йде більше часу ніж на додавання].

Теорема Безу. Залишок від ділення поліному на двочлен дорівнює значенню цього поліному при .

2. Обчислення значень аналітичної функції основується на представленні її у вигляді швидко збіжного ряду Тейлора.

Нехай треба розрахувати значення аналітичної функції на відрізку [a,b] в точці , що належить відрізку з заданою гранично допустимою абсолютною похибкою ε.

- залишковий член у формулі Лагранжа.

, ζ- деяка точка , що строго лежить між і

Отже Q_n(x)+R_n(x^*), де Q_n(x)- n-a частина суми ряду

Q_n(x)=, 0!=1,

R_n(x^*)- значення залишкового члену при

R_n(x^*)=

залишковий член у формі Лагранжа ζ- деяка точка , яка строго лежить між і при . Оскільки похідна неперервна на відрізку [a, b] , то вона обмежена на цьому відрізку , тобто

Отже

- похибка і

(5), - мах. похибка, де . Недолік - нерівномірна точність апроксимації функції на відрізку [a,b].

Приклад: апроксимувати функцію многочленом Тейлора на відрізку [0.1], з абсолютною похибкою ≤ 10^-5. Рішення: вибираємо х₀ = ½, тобто середину відрізку [0,1], щоби мінімізувати величину в формулі (5). Тоді

Згідно (5)

n	2	3	4	5	6
	5.7*10-2	7.1*10-3	7.1*10-4	5.9*10-5	4.3*10-6

Врахуємо

Отже n=6

Алгоритм.

1. вибирають на відрізку [a,b] точку х=с по можливості близьку до і таку, що саму функцію та її похідну легко можна розрахувати при х=с.

2. Представляють похибку 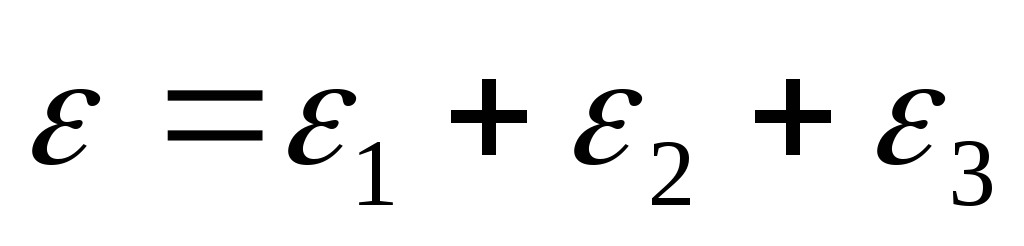, де 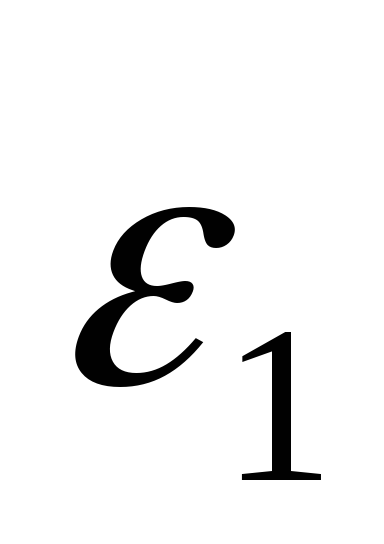- залишкова похибка (похибка методу), 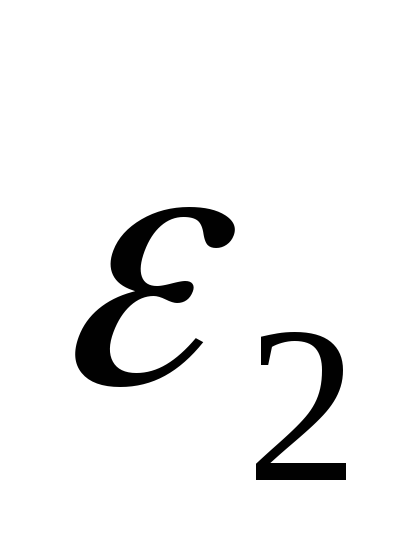- гранично допустима абсолютна похибка обчислення ,- гранично допустима абсолютна похибка заокруглення результату.

На практиці беруть ε= 10^-m, ε₃=0.5*10^-m, а ε₁= ε₂=0.25*10^-m. Якщо похибка кінцевого заокруглення відсутня , то приймають ε₁= ε₂=0.5* 10^-m, ε₃=0.

3. Вибирають число доданків в 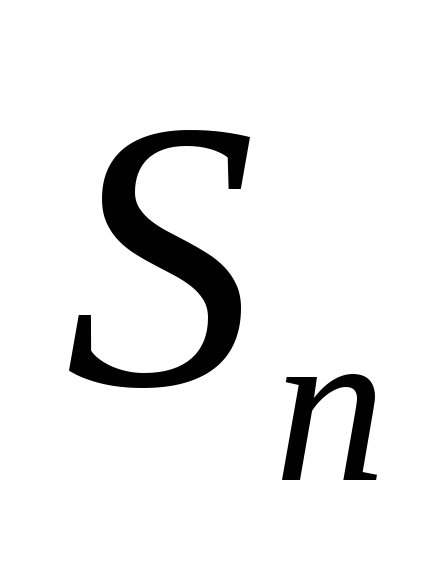так, щоб

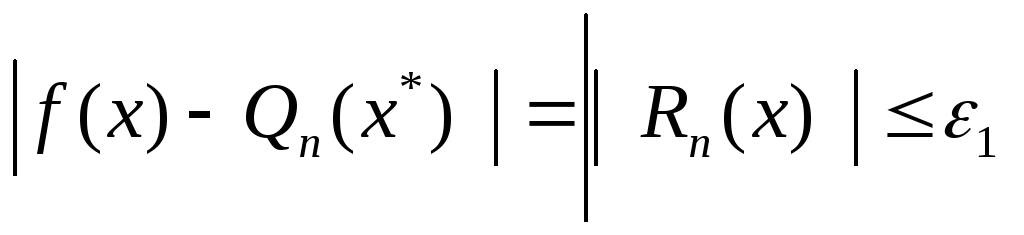
4. Розраховують кожен доданок суми Q_n(x) так щоб наближене значення 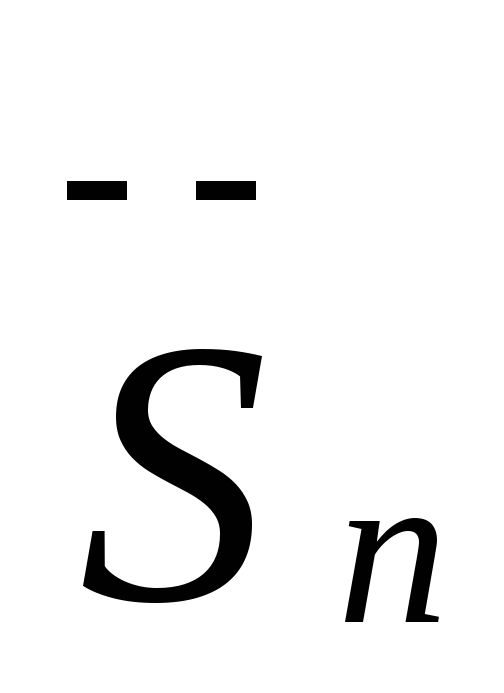відрізнялось від точного 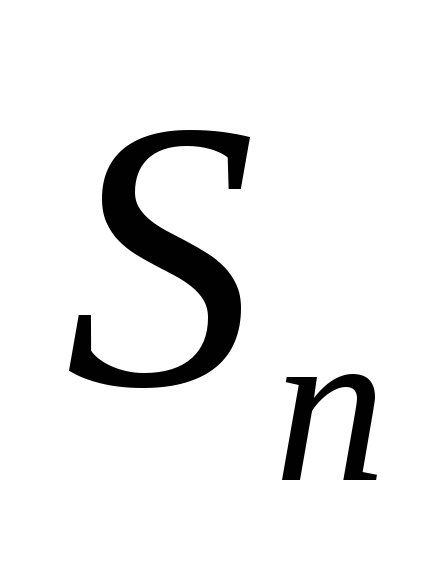не більш ніж на ε₂. За звичай для цього кожен доданок 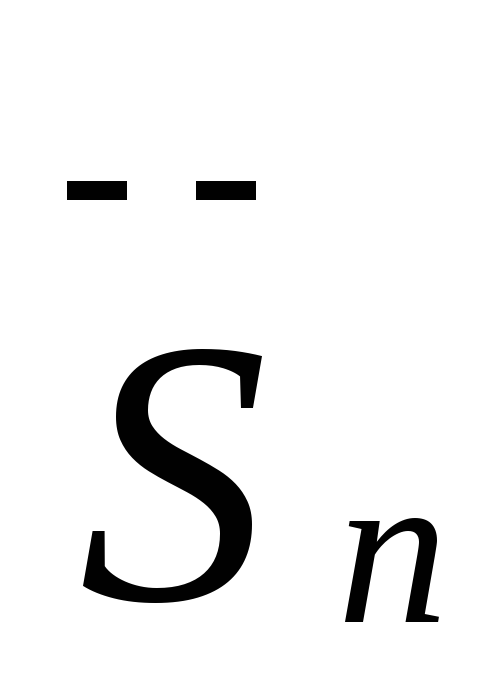з абсолютною похибкою .

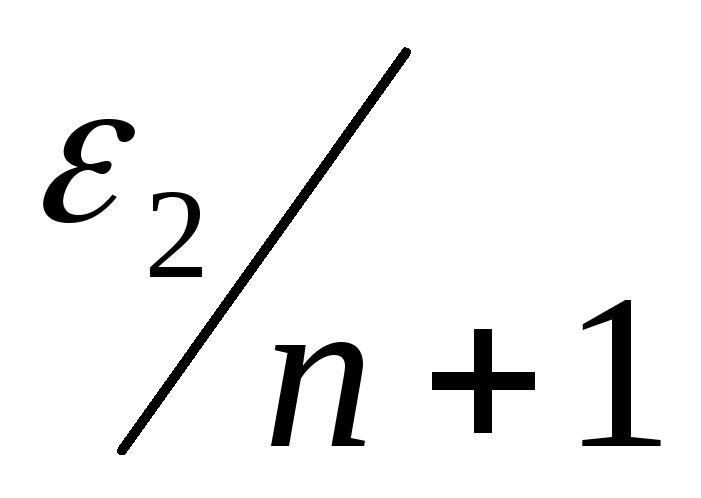5. Отриману в пункті 4 наближену суму 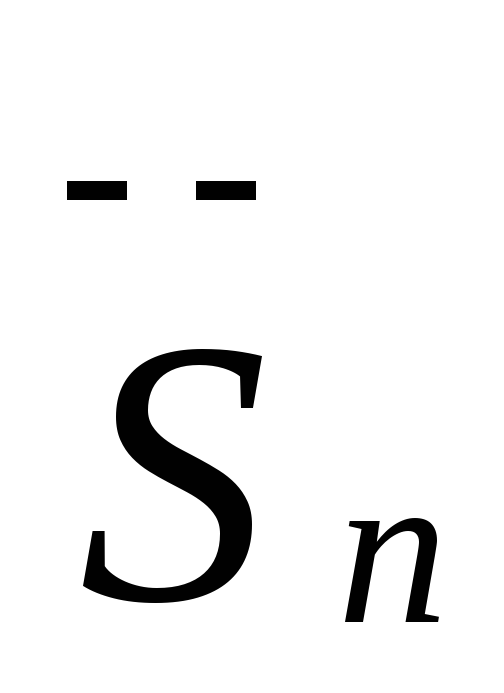заокруглюють якщо ε₃ до.

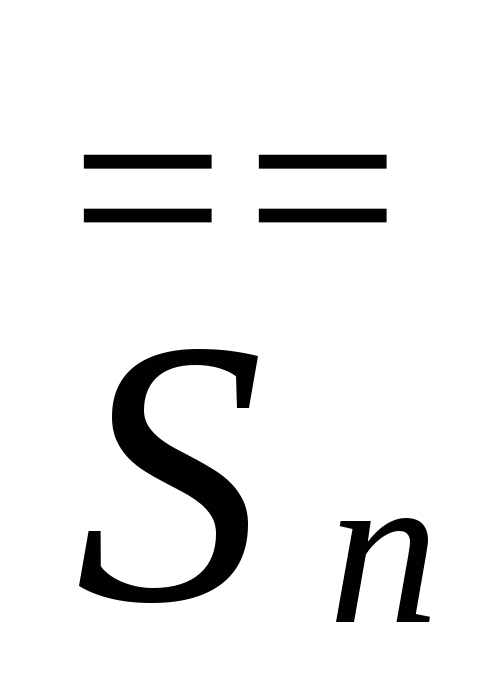6. Записують розв’язок .

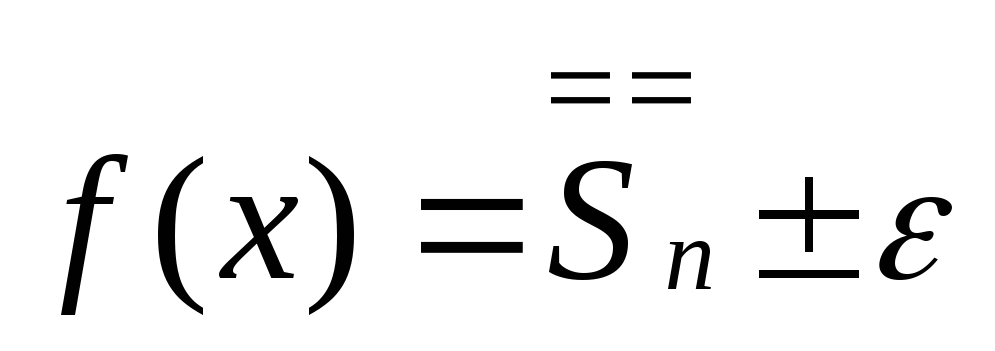3. Ітераційний метод обчислення значень функцій.

(m=2,3) в інтервалі (о,)

Алгоритм:

1. Функцію (1) записують в неявному вигляді і підставляють в отриманий вираз замість 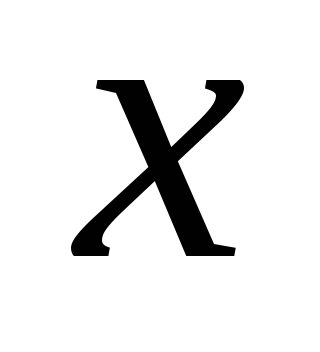його значення :

Розв’язком цього рівняння і буде шукане значення функції .

2. Рівняння (2) розв’язують методом Ньютона: початкове наближення у₀ вибирають так, щоб виконувалась умова 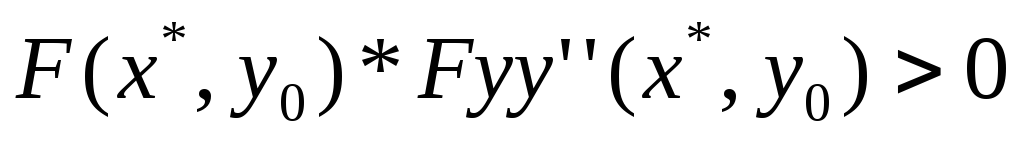(3) , а кожне наступне значення у_n обчислюють за формулою 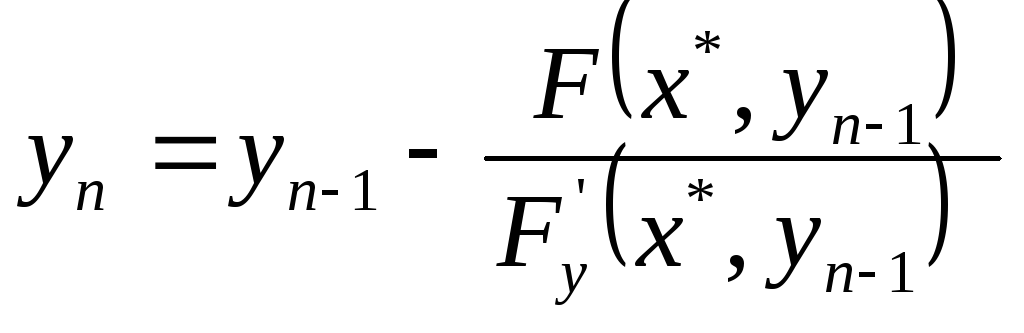(4) (n=1,2…)

Представлення функцію (1) в неявному вигляді (2) можна здійснити безліччю способів. Серед всіх треба вибрати такий, щоб ітераційний процес (4) збігався швидко.

Приклад, умова (3) для кореня буде , а (4)

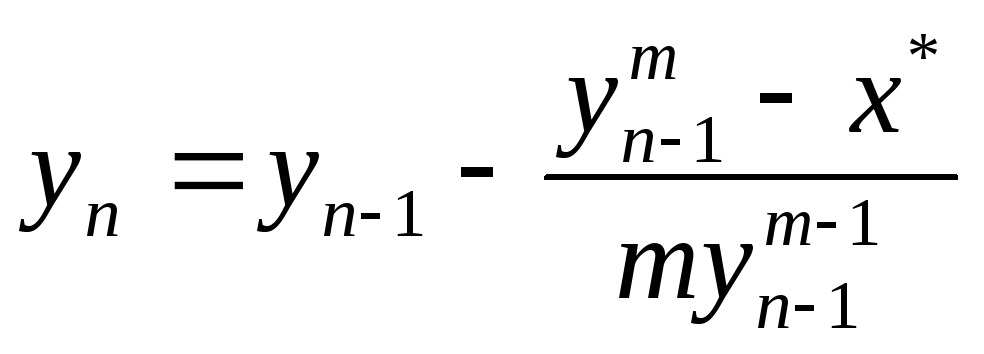
Похибка наближеного значення у_n оцінюється так :

Обчислити е^2.25 з точністю ε=0.01

, 0< - це є формула Тейлора для в околі точки з залишковим членом у формулі Лагранжа. як при великих х ряд Тейлора збігається повільно то значення варто обчислювати у формі . можна розрахувати з будь-якою точністю , тому похибка =0

Похибку заокруглення та обчислення постав.=0,005. Тоді похибка обчислення

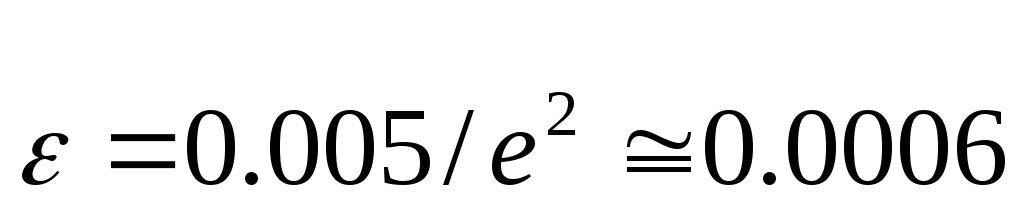
Ми звели обчислення з точністю до обчислення з точністю

Нехай Визначимо n.

Враховуючи , що , отримаємо . Отже , потрібно розрахувати таку суму

S₃= 1+0.25+0.25²/2!+0.25³/3! З абсолютною похибкою 0.0003

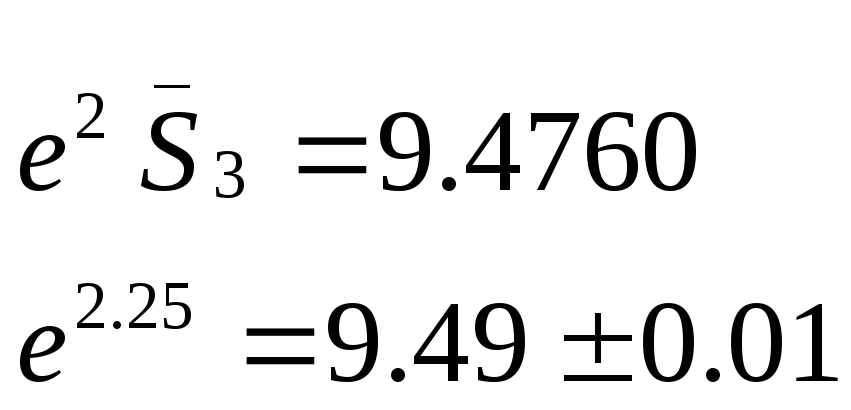ε=0,01

залишковий член у формі Лагранжа ζ- деяка точка , яка строго лежить між і при . Оскільки похідна неперервна на відрізку [a, b] , то вона обмежена на цьому відрізку , тобто

Отже

- похибка і

(5), - мах. похибка, де . Недолік - нерівномірна точність апроксимації функції на відрізку [a,b].

Приклад: апроксимувати функцію многочленом Тейлора на відрізку [0.1], з абсолютною похибкою ≤ 10^-5. Рішення: вибираємо х₀ = ½, тобто середину відрізку [0,1], щоби мінімізувати величину в формулі (5). Тоді

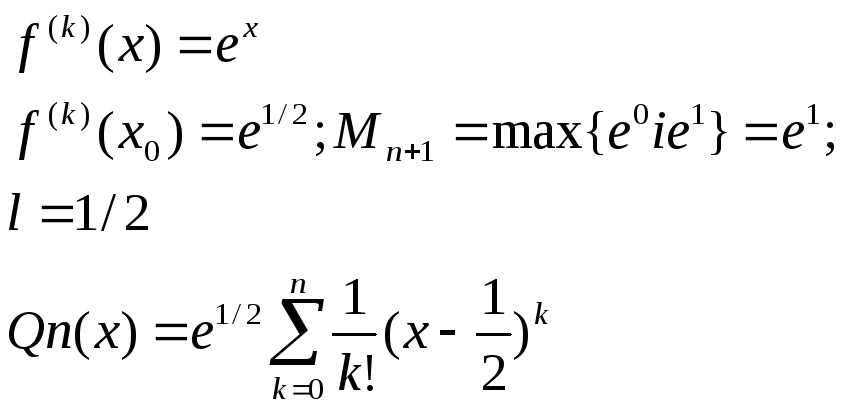
Згідно (5)

n	2	3	4	5	6
	5.7*10-2	7.1*10-3	7.1*10-4	5.9*10-5	4.3*10-6

Врахуємо

Отже n=6