Алгоритми наближення функції
Способи задання функції:
Аналітичний, графічний,
табличний. Основними характеристиками
таблиць є назва функції, об’єм, крок,
кількість вірних знаків табульованої
функції; кількість входів, число
аргументів , кінцеві різниці
),
які записуються між значеннями .
При користувані таблицями основною задачею є знаходження значення функції для тих значень аргументу, які знаходяться між тими , що є в таблиці. Цю задачу називають інтерполяцією
Лінійна інтерполяція:
Схема Ейткіна
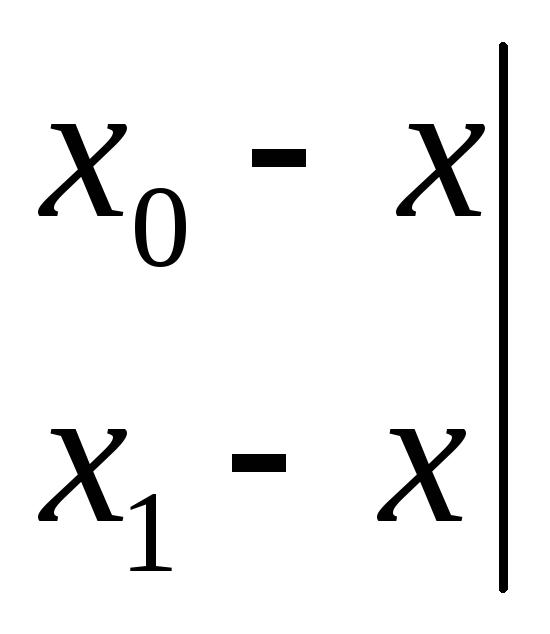визначник
для вузлів х1 і
х0
але можна враховувати
ще інші вузли х2,
х3,
х4
Якщо функція у=f(x) задана , то тим самим будь-якому допустимому значення х співставляється значення у. Але частіше всього можна отримати невелике число значень функції. А для розрахунку функції бажано мати достатню просту аналітичну залежність. Тоді функцію замінюють наближеною формулою φ(х) близькою до f(x) в деякому змісті і зручною для обчислень
Розрізняють два зручних способи вибору наближення функції: інтерполяцію і апроксимацію
Нехай f(x) задана таблицею її значень у=у0, у1, у2...уn в точках х=х0,х1,х2...хn, що називаються вузлами інтерполяції . Задача інтерполяції полягає у виборі такої функції φ(x) , яка б у вузлах хі приймала ті ж значення , що й f(x), тобто φ(xі)=уі . Як правило в якості інтерполюючих функцій вибирають багаточлен. Так як число вузлів дорівнює (n+1) , то степінь інтерполяційного багаточлену дорівнює n.
У багатьох випадках, коли значення функції отримані експериментально і містять похибки, немає необхідності точного спів падання значень φ(x) і f(x) в вузлових точках. Більше того, для практики можна користуватись багаточленах меншого степення m (m<n) або аналітичної залежністю іншого вигляду аби тільки її графік проходив достатньо близько від точок (хі, уі) на всьому проміжку інтервалу зміни х.
Процедура побудови функції виходячи із наперед введеного поняття близькості називається апроксимацією.
В числовому аналізі широке застосування мають три групи апроксимуючих функцій .
1- функції виду 1, х, ...,хn, лінійні комбінації яких народжують клас всіх багаточленів степені m<n
2- тригонометричні функції sin aix i cos aix, що народжують ряди Фур’є та інтеграл Фур’є .
3 – експоненціальна функції
,
що визначають явище розпаду та накопичення
Багаточленна апромаксимація
Питання про критерій близькості:
критерій Чебішева заснований на понятті віддалі як мах величини відхилення функції φ(x) від f(x) у вузлах хі
Якщо ρ1=0, то маємо інтерполяцію. Ще одним критерієм узгодження є
В якості апроксимованої функції вибирають ту , для якої ρ мінімальне. Цей критерій варто використовувати у випадку великої кількості інформації заданої з невисокою точністю. Метод апроксимації заснований на даному критерії часто називають методом найменших квадратів. Вибір методу і критерію повинен бути підпорядкований – необхідній точності.
Інтерполювання за допомогою багаточленів
вибір
конкретного n
визначається властивостями апроксимуючої
функції, точністю, а також вузлами
інтерполяції. Інтерполяційна формула
Ньютона. Потрібно знайти Pn
(x) , що
приймає у вузлах х0,
х1,
... , хn
ті ж значення, що і f(x)
Введемо поняття роздільних різниць:
- розділена різниця першого
порядку
- другого порядку
Багаточлен другої степені
-
лінійна інтерполяція
звідси
інтерполяційний багаточлен Ньютона це:
Pn(x) = f(x0) + A10(x0, x1)(x-x0) + A20(x0, x1, x2)(x-x0)(x – x1) + …+ An0(x0, x1, x2…,xn)(x-x0) (x – x1)… (x – xn-1) (1)
Цей многочлен в точках x0, x1, x2…,xn приймає ті ж зачення, що функція f(x).
Приклад. Приведені в прикладі значення є значеннями функції f(x)=1/(1+x) ; f(2) = 1/3 - точне
-
X
Y
A1
A2
A3
0
1
3
4
1
0.5
0.25
0.2
-0.5
-0.125
-0.05
0.125
0.025
-0.025
Ai розраховується так :
А10= А(x0,x1) = (y1- y0)/ (x1 – x0) = -0.5
А11= А(x1,x2) = (y2 - y1)/ (x2 – x1) = -0.125
А12= А(x2,x3) = (y3- y2)/ (x3 – x2) = -0.05
Елементи стовпця А2
А20= (А11 – А10)/(x2 – x0) = 0.125 m=2 i=0
А21= (А12 – А11)/(x3 – x1) = 0.025
i
А30= (А21 – А20)/(x3 – x0) = - 0.025 m=3 i=0
Отримаємо
P3(x) = 1- 0.5x+ 0.125x(x-1) – 0.025x(x-1)(x-3)
P3(2) = 0.3 – наближено
Для рівновіддалених вузлів розділені різниці розраховуються як:
Аmi = (Аm-1,i+1 - Аm-1,i)/(mh), де m = 1,n-1
h – крок інтерполяції
Тоді (1)
Pn(x) = (...((An0(x-xn-1) + An-1,0)(x - xn-2) + An-2,0)....)(x-x0) +A0;
A0= y1
Створення інтерполяційної формули Ньютона длля великого числа точок пов’язана з тим , що по мірі просування від початкової точки накопичуються похибки зумовлені обчисленням розділених різниць. Із-за втрати точності ввикористання розділених різниць великих порядків є неоправданим.