Оптимізація

Під оптимізацією розуміють вибір найкращого варіанта із багатьох можливих. Це може бути вибір найкоротшого шляху, або найкращого шляху для доставки товару, найшвидшого виконання і т.д.

Задача оптимізації описується деякою функцією f залежною від n- параметрів.

(1)

Параметри від яких залежить функція називаються проектними параметрами, а сама функція називається цільовою. В економіці проектними називають параметри плану. В інженерних та наукових задачах під оптимізацією функції розуміють знаходження їх максимальних та мінімальних значень. Цільова функція може залежати від одного параметра , тоді кажуть, що проводиться одно – мірна оптимізація. Кількість параметрів визначають розмірність задачі оптимізації. Цільова функція не обов’язково задається в аналітичній формі, а може бути задана у вигляді таблиці. Є два види задач оптимізації : умовні та безумовні.

Безумовні задачі – оптимізації – це задачі, в яких визначають оптимальні значення проектних параметрів в деякій області їх значень. На параметри не накладається обмеження.

Якщо на параметри накладаються деякі обмеження, то такі задачі називаються умовними. Обмеження можуть накладатися в 2 – ох формах:

1. У вигляді рівності, що зв’язує проектні параметри.

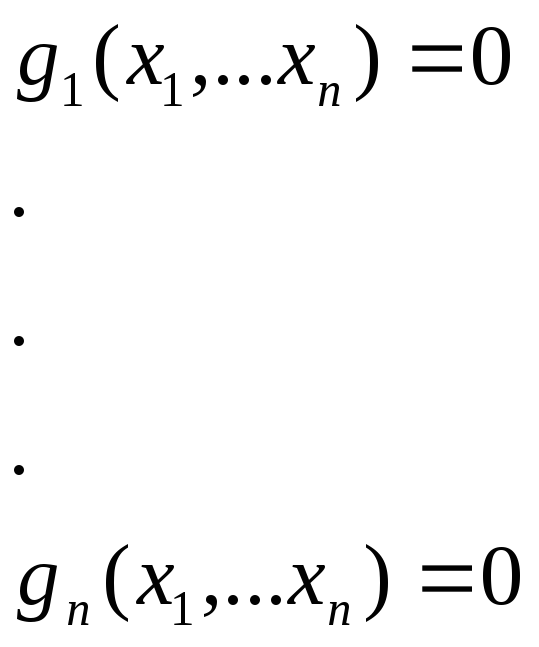
2. На проектні параметри накладаються обмеження у вигляді нерівностей:

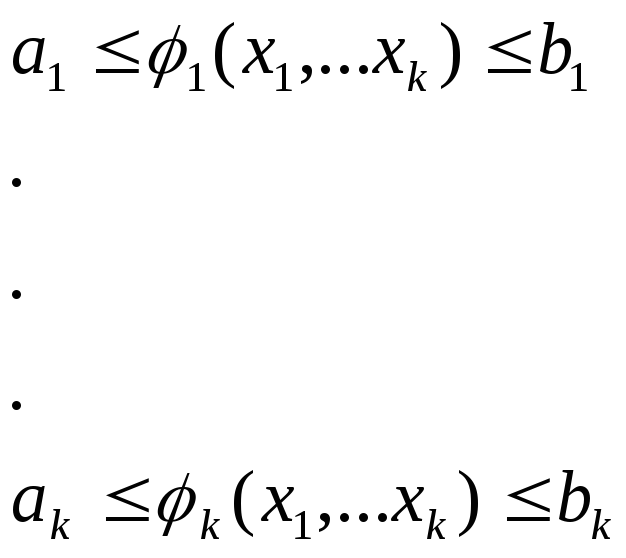
Цільових функцій, які описують дану задачу оптимізації може бути декілька, тоді серед них віддається перевага одній. Тоді кількість параметрів , від яких залежить цільова функція вдається зменшити.

Приклад, нехай треба визначити форму контейнера у вигляді паралелепіпеда, яка потребує найменшої витрати матеріалу. Товщина стінок одинакова.

X₂

X₃

X₁

Площа всіх стінок (1)

Нехай задана 1 умова: його об’єм V=1м³. Це означає, що на проектні параметри цільової функції накладена умова =1 (2). Треба знайти точні параметри х₁,х₂,х₃ при яких значення функції S буде мінімальним!

Із (2) х₃=1/(х₁х₂) (3) в цільову функцію S (1)

Тобто врахування обмеження на проектні параметри дозволило зменшити розмірність задачі оптимізації.

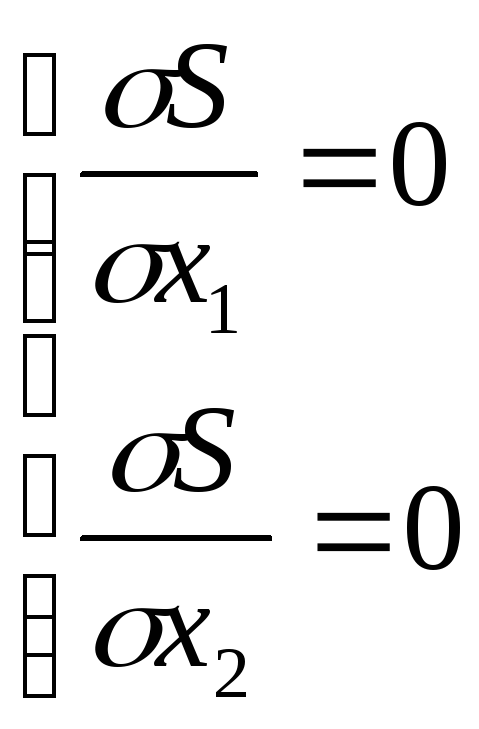
знаходимо х₁ і х₂ в (3) х₃

, =1 х₁=1→ х₃=1 → х₂=1

Одномірна оптимізація.

Ця задача формулюється так: на відрізку [a,b] задана деяка функція f(x). Треба знайти її максимальне або мінімальне значення. Як правило, шукають мінімальне значення функції. Задача знаходження максимальної функції зводиться до знаходження мінімальної функції, якщо знак цільової функції змінити на протилежний.

Існування мінімуму функції випливає з теореми Веєрштраса: якщо функція неперервна на [a,b], то вона обов’язково приймає на ньому максимальне або мінімальне значення, тобто існує така точка х, що виконується

Просто знаходити мінімум функції, якщо вона диференційована і задана в простій аналітичній формі. Тоді і знаходити точки екстремуму . Мінімум може знаходитись або в точці екстремуму або на кінцях відрізку.

Але аналітично знайти мінімальну функцію вдається знайти в рідкісних випадках. Переважно це роблять за допомогою ПК.

Нехай функція f(x) задана на [a,b] і нехай відомо, що на цьому відрізку знаходиться мінімальна функція. Відрізок [a,b], на якому знаходиться мінімум функції називається інтервалом невизначеності. В задачах оптимізації ставиться вимога знаходження мінімальної функції з точністю ε. Це означає, що b-a<ε.

Найбільш простий метод знаходження мінімуму такий: Відрізок [a,b] розбивають на дрібні відрізки з кроком , де x_i=a + i*h , і=0,1…n.

Обчислюють значення функції у всіх точках х_і. Це означає, що інтервал невизначеності має розмір відрізка . Такий метод називається методом пошуку. Він вимагає обчислення значення функції у великій кількості точок.

Є кілька методів ефективного знаходження мінімуму функції. Розглянемо один із них, який вимагає меншої кількості обчислень значень функції.

Метод золотого перетину.

Метод золотого перетину полягає в послідовному знаходженню інтервалів невизначеності. [a₀,b₀],….. [a_k,b_k] при мінімальних затратах на обчислення значень функції.

Геометрично: Нехай початковий інтервал невизначеності - відрізок [a₀,b₀]. В середині відрізку обчислюємо значення функції в двох точках х₁ і х₂. Нехай . Тоді відрізок [х₂,b] можна відкинути і продовжити пошук мінімуму на відрізку [a₀,х₂]. Відрізок [a₀,х₂] – це наступний інтервал невизначеності - [a₁,b₁].

На ньому знаходять значення функції в точці х₃. Нехай , тоді відрізок [a₀,х₃] можна відкинути і продовжити пошук мінімуму на відрізку [х₃,b₁]. Це продовжуємо до тих пір, поки інтервал невизначеності не досягне заданої величини. Тільки на 1 – ому кроці значення функції обчислюють в 2 – ох точках х₁ і х₂. На всіх наступних кроках функцію обчислюють тільки в одній точці.

Ідея методу полягає в спеціальному вибору цієї точки на черговому інтервалі невизначеності. Нехай заданий відрізок довжиною l. Поділимо його на 2 частини, причому l₁> l₂

l

l=l₁+l₂

Точкою золотого перетину називається точка, яка ділить відрізок так, що відношення довжини . Звідси

, | :

або

Нас цікавить тільки “+” корінь. Тоді

В нашому видку точки вибираємо так, що

Аналогічно на наступному кроці:

. Виберемо так ,щоб

Тобто отримуємо зв'язок між інтервалами невизначеності

,

На кожному кроці

Координати відрізків на k+1 кроці визначаються так

В ролі точки мінімуму можна взяти , або

Термін – апроксимація – означає наближення. Інтерполяція є частковим випадком точкової апроксимації. Значення функції можна знаходити не тільки всередині відрізка , а і за межами і . Цей процес називається екстраполяцією.

Задача інтерполяції формулюється так : треба знайти такий многочлен φ(х), значення якого у всіх точках х_і співпадає із значеннями табличних даних чи експериментальних φ(х_і)=у_і і=0,1...n (1)

Вважається , що серед всіх точок х_і немає співпадаючих х_і х_к , при ік . Многочлен φ(х)=а₀+а₁х+а₂х²+...+а_mх^m (2) називається інтерполюючим многочленом, а точки х_і – називаються вузлами інтерполяції.

Умову (1) записують для всіх n – експериментальних точок і отримують систему n- рівнянь. Розв’язуючи її знайдемо а₀,а₁...а_n. Випадок , коли степінь многочлена φ(х) m=n називається глобальною інтерполяцією. В цьому випадку многочлен φ(х) проходить через всі експериментальні точки. Многочленом φ(х) можна наближувати експериментальні дані не на всьому відрізку , а лише на окремих ділянках. Така інтерполяція називається кусковою або локальною. Значення функції в проміжних точках , які не знайдені на експерименті , після того як знайдений загальний вигляд інтерполяційного многочлена , вже можна знайти. Тобто ми знаємо многочлен φ(х) , треба знайти φ(х_р) .

Лінійна інтерполяція є видом локальної інтерполяції . Нехай задані таблиці значень , і=0,1...n , тобто для сукупності значень аргумента задані відповідні значення функції. Вони можуть бути результатом обчислень або експерименту . Ставиться така задача : для деякого проміжного значення аргумента х_ξ, яке не належить табличним значенням функції , і =1,...n , треба знайти відповідне значення функції , і =1,...n

Алгоритм знаходження відповідного значення функції у випадку лінійної інтерполяції такий : знаходять дві сусідні точки (х_і-1, у_і-1) та (х_і, у_і) такі , що . Для цих двох точок записують рівняння прямої (1)

= = в

Звідси знаходять рівняння прямої , яка з’єднує дві точки , (2) де ;

Маючи рівняння (2), яке наближає експериментальну залежність на відрізку [х_і-1, х_і] легко знайти значення функції для заданого значення аргументу. Лінійна інтерполяція означає, що експериментальна залежність на кожному відрізку [х_і-1, х_і] наближено замінюється лінійною. На всьому відрізку [х₀, х_n] експериментальна залежність наближується ламаною лінією.

Квадратична інтерполяція

y=a_ix²+b_ix+ c_i

_αi

Y y_i y₁

y₀ X x₀ x₁ x_і

Лінійна та квадратична є локальними інтерполяціями. Це означає, що експериментальне значення функції наближається рівнянням прямої чи параболи на деяких локальних ділянках. На цих ділянках рівняння прямої чи параболи різні.

Program Linia;

Label lab1 ,lab2,

Const n=20

Var x: array [1..n] of real;

Y: array [1..n] of real;

I, k : integer

Ak, bk, a, f : real;

Begin

For i:=1 to n do

Begin

Write (‘x(’,I,’)=’); readln (x[i]),

Write (‘y(’,I,’)=’); readln (y[i]),

Write (‘введіть значення x=’); readln (a);

End;

K:=1;

Lab1: k:=k+1;

If (a>x[k-1]) and (a<x(k)) then begin

Ak: =(y[k]-y[k-1])/( (x[k]-x[k-1]);

Bk:= (y[k-1]-ak*x[k-1]);

F:=ak*a+bk

Go to lab2; end

Else go to lab1;

Lab2:

Write (‘a=’,a,’y=’,f);

End

Локальне згладжування даних

Так як експериментальні дані містять помилки, то використовувати точні значення експериментальних даних недоцільно. Їх стараються згладити. Це згладжування роблять для кожної експериментальної точки х_і. По обидві сторони від експериментальної точки х_і вибирають точки к-парне. Тобто розглядають х_і–к/2,.. х_і-1, х_і, х_і+1.. х_і+к/2 і відповідно у_{і –к/2},.. у_і-1, у_і, у_і+1.. у_і+к/2. Використовуючи ці точки будують многочлен степені m<=k. Цей многочлен в загальному випадку не обов’язково проходить через всі експериментальні точки. Значення многочлена в точці х_і і є згладженим значенням функції – . Таке згладження роблять для всіх точок х_і. Можна робити також і повторне згладження , але це не завжди доцільно , так як воно може спотворити експериментальні дані .

Найкращі формули, які використовуються для згладження такі: m=1,k=2→ =1/3 (y_i-1+y_i+y_i+1) ; m=1,k=4→ =1/5 (y_i-2+y_i-1+y_i+y_i+1+y_i+2)

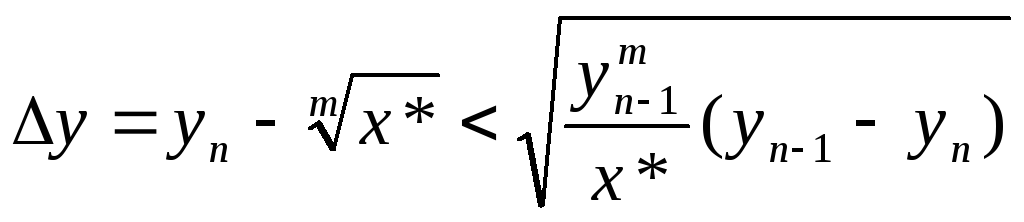(4)

або (5) ? з точністю ε=10^-4.

Вибираємо у₀=3,4>; із (4)