
- •В наведеному прикладі
- •Вірні значущі цифри.
- •Похибки суми та різниці
- •Похибка добутку
- •Похибки частки та число вірних знаків частки.
- •Похибки степеня та кореня.
- •Правила підрахування цифр.
- •Розрахунок похибок функцій багатьох змінних.
- •Визначення допустимої похибки аргументів по допустимій похибці функцій.
- •Точність представлення чисел в Комп'ютері
- •Форми представлення 2-их чисел в еоп
- •Похибки представлення чисел.
- •Стійкість, коректність та збіжність.
- •Числове інтегрування
- •Формула прямокутників
- •Формула трапеції
- •Формула сімпсона
- •Похибки
- •Теорема Больцано-Коші
- •Алгоритми відділення коренів рівняння
- •Алгоритми уточнення коренів.
- •1)Алгоритм уточнення кореня методом половинного ділення.
- •Програма методу перебору
- •Алгоритм уточнення кореня рівняння методом половинного ділення
- •Алгоритм уточнення кореня методом хорд
- •Mетод дотичних
- •Метод ітерацій (метод послідовних наближень)
- •Числові методи розв’язування систем лінійних рівнянь
- •Алгоритм
- •Алгоритм для системи нормального вигляду
- •Метод ітерації
- •Метод ітерацій Зейделя (ітерації)
- •Оптимізація
- •Алгоритми наближення функції
- •Інтерполяційний багаточлен Лангранжа
- •Коефіцієнти Лангранжа які задовільняють умовам:
- •Блок-схема алгоритму
- •Апромаксимація. Метод найменших квадратів
Алгоритм
АХ = В
 Введемо розширену матрицю
Введемо розширену матрицю
 a11
a12 . . . a1n
b1
a11
a12 . . . a1n
b1
a21 a22 . . . a2n b2
.
(А|B) = .
an1 an2 . . . ann bn
A(N,N); B (N)
Розв’язок X(N) розмістимо в В.
-
Ділимо перший рядок (А|B) на а11 , потім множимо його послідовно на ак1 (k =2...n ) і віднімаємо його від k-ого рядка. Після цього отримаємо наступну матрицю:
-
1
 a
a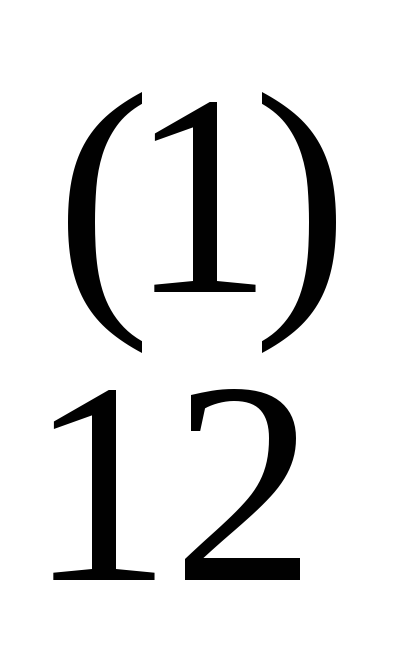 ... a
... a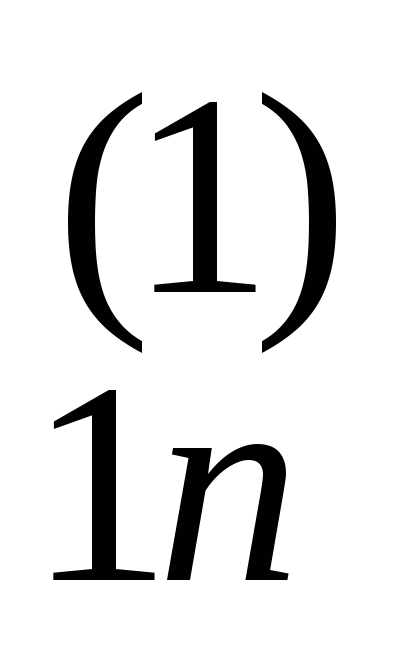 b
b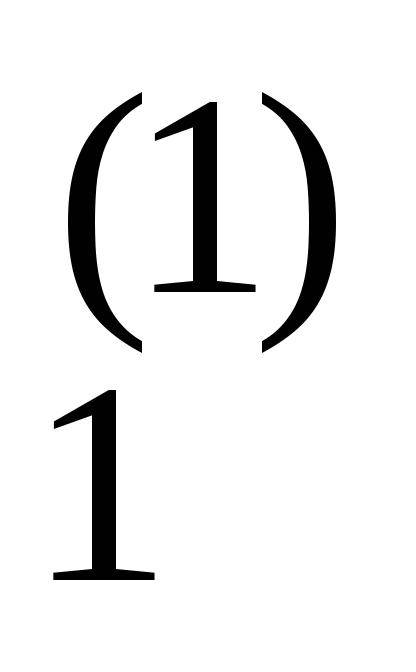 0 a
0 a ... a
... a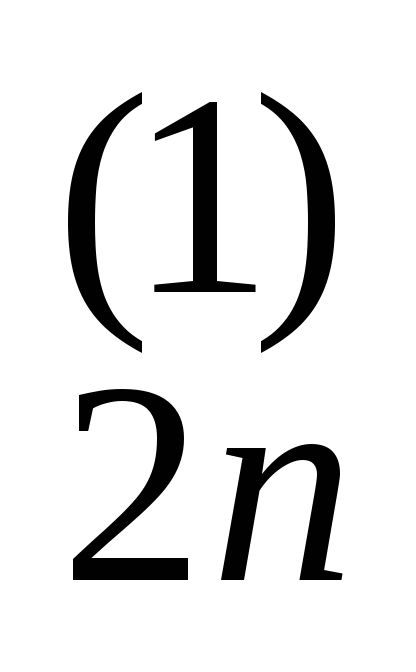 b
b .
.
.
0 a
.
.
.
0 a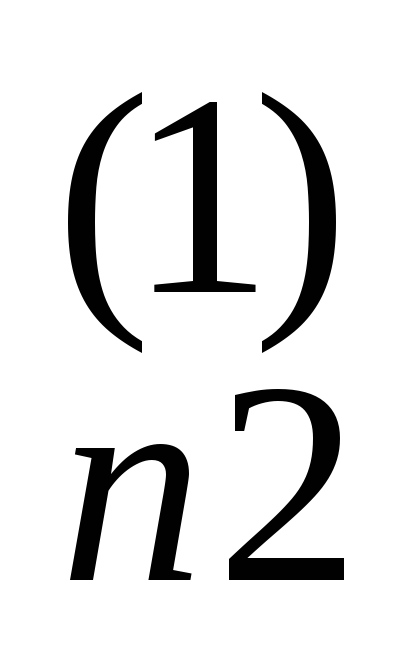 ... a
... a b
b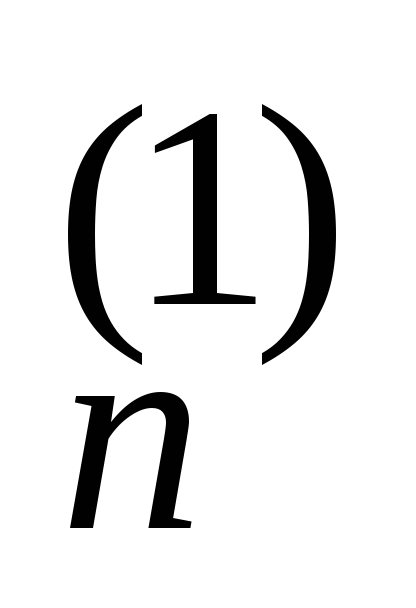
-
Елементи другого рядка ділимо на а
 , потім множимо на а
, потім множимо на а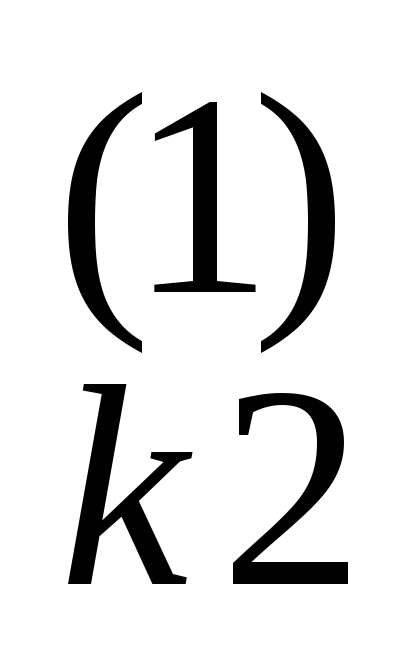 (k = 3…n)
і віднімаємо від k-ого
рядка.
(k = 3…n)
і віднімаємо від k-ого
рядка. -
П
 родовжуємо
цей процес до тих пір, поки ця процедура
не повториться (n-1)
раз. Тоді отримаємо:
1 a
родовжуємо
цей процес до тих пір, поки ця процедура
не повториться (n-1)
раз. Тоді отримаємо:
1 a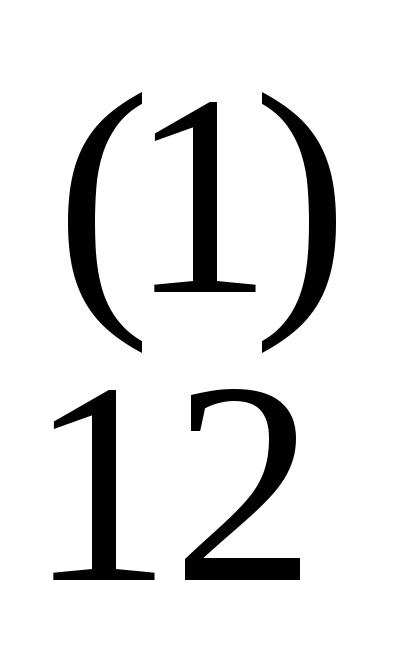 ... a
... a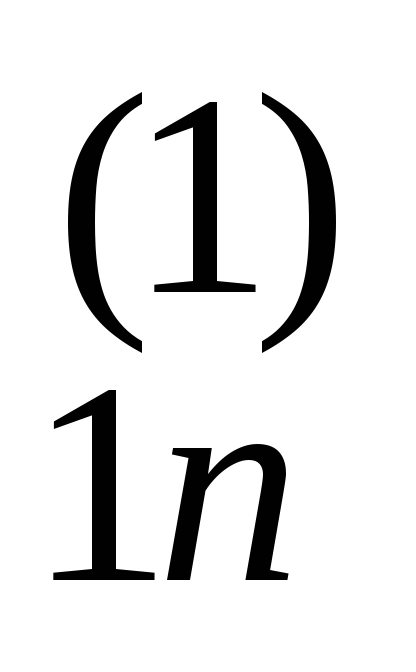 b
b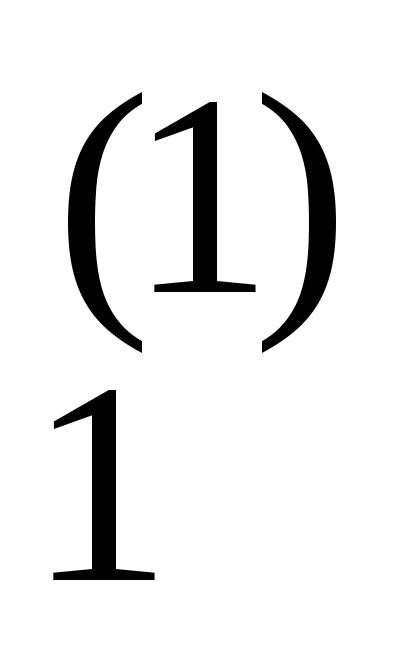 0 1 a
0 1 a ... a
... a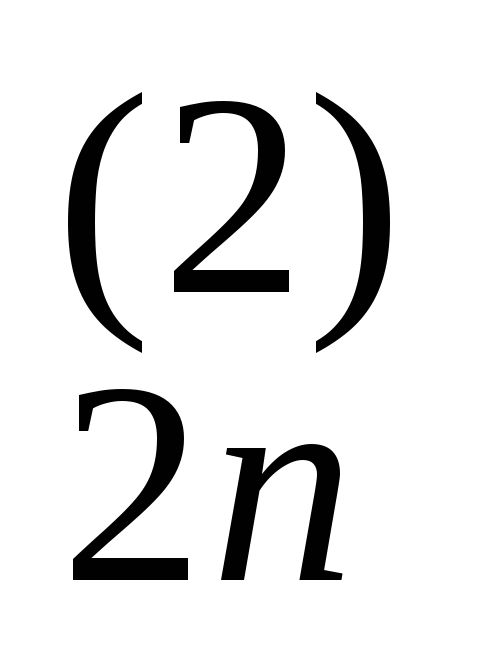 b
b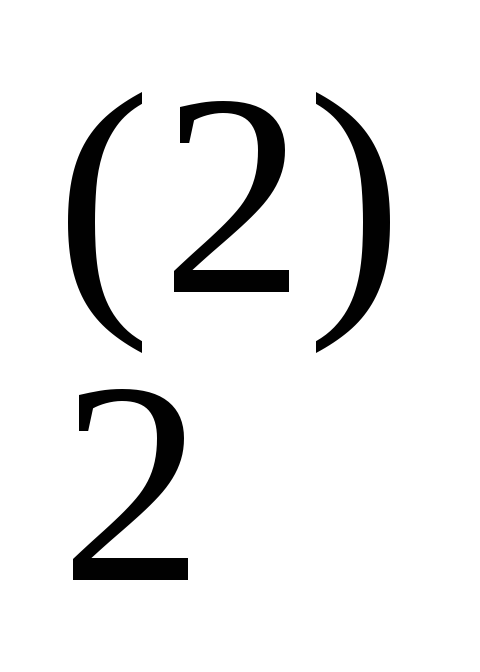 0
0 1 ... a
0
0 1 ... a b
b .
.
.
0
0 0 ... 1 a
.
.
.
0
0 0 ... 1 a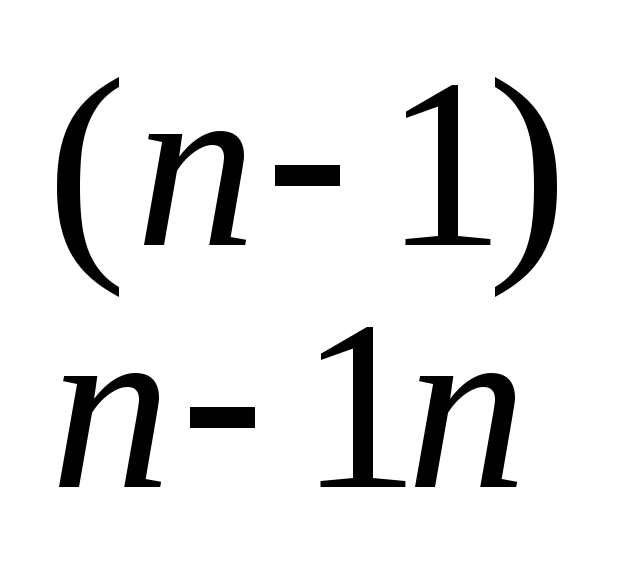 b
b 0 0 0 … 0 1 b
0 0 0 … 0 1 b На цьому прямий хід методу Гауса
закінчується.
На цьому прямий хід методу Гауса
закінчується. -
Виконуємо обернений хід метода Гауса. В (n-1) рядок підставляємо значення хn і знаходимо хn-1 і т.д. за формулами
Правилом Крамера вже для n=4 не користуються, бо число операцій :
N (n) = (n2-1) n! +n , а для Гауса
N (n) =
![]() (n2+3n
- 1)
(n2+3n
- 1)
-
Тобто при:
n = 5
n=10
По Крамеру
N = 2885
N = 360∙106
По Гаусу
N = 65
N = 430
Метод Гауса – в теорії числових методів показується, що при виконанні прямого ходу методу Гауса треба виконати n3/2 – додавань, ~ n3/3 – множень, ~ n2/2 – ділень. На оберненому ході методу Гауса ~n2/2 – додавань, ~ n2/2 – множень, ~ n – ділень. Отже, приведення матриці до трикутного вигляду на порядок складніше ніж знаходження невідомих.
При розробці алгоритму обов’язково треба перевірити а11≠0. Якщо а11=0, тоді серед коефіцієнтів аі1 (і=2,3,...,n) шукають відмінний від нуля коефіцієнт аі1. Міняють це рівняння з першим. Такий коефіцієнт обов’язково знайдеться, інакше матриця вироджена, тобто detA=0.
Серед коефіцієнтів, на які відбувається ділення, можуть бути дуже малі, тоді при діленні на них можуть виникнути переповнення, що приведе до різкого зростання похибок.
При обчисленні визначника, треба виконати (n-1)n! Операцій множення і (n!-1) – операцій додавання. Отже всіх операцій N=n!-1+(n-1)n!=nn!-1nn!
|
n |
3 |
10 |
20 |
|
N |
17 |
3.6107 |
51019 |
|
час |
|
6 хв. |
1.41011год5109діб |
Якщо швидкодія 100000 оп/сек.
Тому звичайні методи для обчислення
визначника малоефективні. Тому стараються
використовувати більш економні методи.
Зручно використовувати прямий хід
Гауса, тобто приводити матрицю до
трикутного вигляду. Визначник при цьому
не міняється, може змінитися тільки
його знак і detA= ![]() акк
, де акк – діагональні
елементи приведеної до ∆-вигляду
матриці. Добуток береться зі знаком
,,+’’, якщо кількість переставлених
рядків парна, і ,,-’’, якщо непарна (при
приведенні до ∆-вигляду).
акк
, де акк – діагональні
елементи приведеної до ∆-вигляду
матриці. Добуток береться зі знаком
,,+’’, якщо кількість переставлених
рядків парна, і ,,-’’, якщо непарна (при
приведенні до ∆-вигляду).
О бчислення
оберненої матриці
бчислення
оберненої матриці
1 k=j
![]() aik
zkj
= ij
0 ij
aik
zkj
= ij
0 ij
Для отримання оберненої матриці треба n-раз розв’язати початкову систему. Після кожного розв’язку системи знаходиться один стовпчик оберненої матриці. Наприклад, для знаходження стовпчика оберненої матриці номер j, тобто z1j,…,znj треба розв’язати систему таких лінійних рівнянь:
 a11z1j
+ a12z2j
+…+ a1nznj
= 0
a11z1j
+ a12z2j
+…+ a1nznj
= 0
.
.
.
aj1z1j + aj2z2j +…+ ajnznj = 1 (2)
.
.
.
an1z1j + an2z2j +…+ annznj = 0
Щоб уникнути цього використовують модифікацію метода Гауса. Одну з таких модифікацій називають методом Гауса з вибором головного елемента в стовпці. Його відмінність від розглянутого метода Гауса в тому, що на кожному кроці шукається максимальний елемент в стовпці. Нехай на кожному кроці отримується діагональний елемент акк(к-1). Серед всіх елементів, які лежать вище шукаємо max: max aк(к-1).
Нехай цей елемент в рівнянні арк(к-1). Міняємо місцями р і k-е рівняння. Цю операцію повторюють на кожному кроці.
В ролі невідомих виступає стовпчик zij. В правій частині один стоїть тільки в z=j. Таких систем треба записати n-штук. Тут зручно проводити обчислення так як матриця aij – не міняється. Тому до трикутного вигляду систему приводять один раз. Для знаходження відповідного стовпчика використовують обернений хід методу Гауса. Цей метод ефективніший ніж метод:
(aij)-1
=
![]() , де
Aji
– алгебраїчне доповнення до aij
в початковій матриці. Таким методом для
знаходження оберненої матриці треба
виконати ~ n2n!
операцій. А описаний метод з
розв'язком систем лінійних рівнянь
вимагає тільки ~ в 3 рази більше арифметичних
операцій ніж приведення системи до
трикутного вигляду.
, де
Aji
– алгебраїчне доповнення до aij
в початковій матриці. Таким методом для
знаходження оберненої матриці треба
виконати ~ n2n!
операцій. А описаний метод з
розв'язком систем лінійних рівнянь
вимагає тільки ~ в 3 рази більше арифметичних
операцій ніж приведення системи до
трикутного вигляду.
Важливим є питання точності отриманих розв’язків. Її характеризують двома величинами:
Похибка, яка рівна різниці між отриманим розв’язком і точним. При практичному розв’язуванні систем лінійних рівнянь за характеристику точності беруть нев’язку (величина, що дорівнює різниці між правою і лівою частиною рівняння, в яке підставляються розв’язки). Похибка і нев’язка r взаємозв’язані. Якщо = 0, то r = 0. Але обернене твердження не завжди справедливе. Нев’язка в практичних розрахунках повинна бути 10-4 10-6.
Метод ітерацій
Цей метод дозволяє отримати збіжну послідовність наближених значень. Не потрібно контролювати проміжні обчислення, тому що окремі помилки на будь-якому кроці ітерацій не деформують кінцевий результат, хоч можуть процес обчислення зробити довшим, тобто це метод – самовиправляючий.
![]() aijxj
= bi,
aii
≠ 0, визначник системи ≠
0
aijxj
= bi,
aii
≠ 0, визначник системи ≠
0
Виразимо з першого рівняння x1, з другого x2 і т.д. Поділивши рівняння на аіі отримаємо еквівалентну систему:
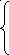 x1
= β1+α12x2+α13x3+…+α1nxni
x1
= β1+α12x2+α13x3+…+α1nxni
x2 = β2+α21x2+α23x3+…+α2nxn
…
xn = βn+αn1x2+αn2x3+…+α n,n-1xn-1, де

- aij /aii , при i ≠ j
βi = bi/ aii ; αi =
0, при i = j
або xi
= βi
+![]() αijxj
(*)
αijxj
(*)
назвемо її системою нормального виду.
Будемо розв'язувати її методом послідовних наближень. За нульове наближення візьмемо :
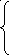 x1(0)
= β1
x1(0)
= β1
x2(0) = β2
 …
…
xn(0) = βn
і підставимо в праву частину (*). Отримаємо:
xi(1)
= βi
+
![]() αijxj(0)
, потім аналогічно
αijxj(0)
, потім аналогічно
xi(2)
= βi
+
![]() αijxj(1)
αijxj(1)

 Робочі формули методу ітерацій
Робочі формули методу ітерацій
x i(0)
= βi
i(0)
= βi
xi(k+1)
= βi
+
![]() αijxj(k)
αijxj(k)
αii = 0; i= 1,n ; k=0,1,2,…
Збіжність?! Якщо
![]() |αij|
< 1 (i=1,n)
або |аij|
>
|αij|
< 1 (i=1,n)
або |аij|
>
![]() |аij|
(i=1,n),
то метод ітерацій для всіх рядків буде
збіжним.
|аij|
(i=1,n),
то метод ітерацій для всіх рядків буде
збіжним.
При обчисленні на машині процес ітерації закінчують, якщо
|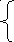 x
x![]() - x
- x![]() |
≤
|
≤![]() •ε
(i=1, n)
•ε
(i=1, n)
q=![]()
![]() |αij|
< 1
|αij|
< 1
Доводять, що тоді |x![]() - x
- x![]() |
≤ ε
|
≤ ε
