Численні методи.-М.: Наука 1987

Бахвалов Н.С., Жидков Н.П., Кобельков

Точні та наближені числа.

Джерела та класифікація похибок

В практиці обчислень під наближеним числом а розуміють число, що незначно відрізняється від точного числа А і замінює його в обчисленнях.

Розв’язок більшості практичних задач умовно проводиться в два етапи:

1. математичне описання досліджуваної проблеми

2. розв’язок сформульованої мат. задачі

На 1-му етапі зустрічаються 2 характерних джерела похибок:

1) процеси, що реально протікають не завжди можна описати математично, а введені спрощення дають можливість отримати лише більш-менш ідеалізовані моделі;

2) неточність задання початкових параметрів, які отримують, як правило, із експерименту, який завжди дає лиш наближений результат.

У відповідності до цього сумарна похибка мат. моделі та початкових даних об’єднується в похибку вхідної інформації. ЇЇ часто називають неусуненою похибкою.

На 2-му етапі отримати точний розв’язок мат. задачі не можливо, незалежно від того чи він знаходиться аналітично чи на ЕОМ.

В практичних розрахунках використовуються методи наближеного розв’язку, і в першу чергу, числові. Така вимушена заміна точного розв’язку на наближений породжує похибку методу або похибку апроксимації.

Нарешті, в процесі розв’язку задачі відбувається заокруглення вхідних даних, проміжних та кінцевих результатів. Ці похибки, то похибки, що виникають при виконанні арифметичних операцій з наближеними числами переносяться на результат обчислень і утворюють так звану обчислювальну похибку або похибку заокруглень або інструментальну.

Виходячи із цього при постановці задачі або вказують необхідну точність розв’язку, тобто задають максимально допустиму похибку в процесі всіх обчислень, або обмежуються вимогами підрахунку сумарної похибки результату. Тому при роботі з наближеними числами необхідно уміти розв’язувати такі задачі:

1. давати мат. характеристики точності наближених чисел;

2. знаючи степінь точності вхідних даних оцінювати степінь точності результату;

3. вибрати вхідні дані з таким степенем точності, щоб забезпечити заданий степінь точності результату;

4. оптимальним чином будувати обчислювальний процес, щоб не проводити розрахунків, які впливають на точні цифри результату.

Десятковий запис та заокруглення чисел.

Будь-яке десяткове число а можна записати у вигляді скінченого чи нескінченого десяткового дробу

а = ₁*10^m + ₂*10^m-1 +……+ _n*10^m-n+1+….., (1)

де _і – цифри числа, ₁ ≠ 0, а m – старший десятковий розряд числа а, n – розряд

n = 1234 5678

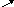10^3-2+1 10^3-4+1 10^3-8+1

1905,0778 = 1·10³ + 9·10² + 0·10¹ + 5·10⁰ + 7·10^-2 + 7·10^-3 + 8·10^-4

10^m-n+1 – називається ціною розряду.

Правила заокруглення:

1. Якщо цифри, що відкидаються є більшими половини останнього залишеного розряду то остання цифра, що залишається підсилюється. Якщо ні, то просто відкидається 12,7852 → 12,8; 394,261 → 394; 6,265001 → 6,27; ;; → 6,27, тому що .

2. Якщо цифри, що відкидаються складають число, що дорівнює половині, то остання цифра, що залишається, підсилюється, якщо вона непарна і залишається без змін, якщо парна. Це правило ще називають правилом парної цифри:

147,5 → 148

148,5 → 148

В деяких випадках, просто відкидають лишні цифри при заокругленні.

Абсолютна та відносна похибки.

Нехай А – точне число, а – його наближене значення. Якщо а < А, то а – є наближеним значенням числа А за недостачею; якщо а > А наближеним значенням числа А за надлишком.

А – а називається помилкою або похибкою. Величину похибки А – а і навіть її знак визначити неможливо, тому що невідоме точне число А. Тому замість самої похибки користуються верхньою границею її абсолютної величини.

Отже, абсолютною похибкою наближеного числа а називається величина , що задовольняє .

Абсолютна похибка – це є верхня межа відхилення точного числа А від наближеного

або (2')

. (3)

На практиці часто використовують вираз типу: „з точністю до 0,01”, „ з точністю до 1 см”. Це означає, що абсолютна похибка = 0,01 чи 1 см.

Приклад 1. Довжину відрізка L виміряли з точністю до 0,05 см і отримали l = 18,4 см. Тут . Згідно (3) . А точна величина довжини відрізку згідно (2') знаходиться в межах 18,35 ≤ L ≤ 18,45.

Приклад 2. Довжину L вимірювали за допомогою лінійки з ціною поділки 0,1 см. Нехай точне значення знаходиться між 4,6 і 4,7 см. Наближене значення варто взяти l = 4,65. Абсолютною похибкою буде половина ціни поділки лінійки.

Абсолютна похибка відтворює лише кількісну сторону похибки, але не якісну, тобто не вказує на те, чи добре, чи погано проведено вимірювання чи розрахунки.

Дійсно, при вимірюванні одною і тією ж лінійкою з ціною поділки 1 см довжини та товщини дошки стола отримаємо результати в см: d = 2 ± 0,5см і

l = 100 ± 0,5 см. Абсолютні похибки однакові – 0,5 см. Але, очевидно, що 2-е вимірювання проведено більш точно ніж перше. Для того, щоб оцінити якість проведених вимірювань чи обчислень, вводять поняття відносної похибки: а ≠ 0 або ,

а ≠ 0 (4) і (3) стане .

Відносну похибку іноді зображають в %.

В наведеному прикладі

або 25%

або 0,5%.

Величину похибки прийнято заокруглювати до 1 ÷ 2 значущих цифр.

Приклад. Оцінити, в якому випадку якість обчислень вища:

а₁ = 13/19 ≈ 0,684 чи

Для знаходження абсолютних похибок беремо числа а₁ і а₂ з більшою кількістю десяткових знаків: і . Визначимо абсолютні похибки з надлишком:

- якість вища.

Вірні значущі цифри.

Значущими цифрами числа називаються всі його цифри, окрім нулів, що знаходяться з ліва від першої відмінної від нуля цифри. Нулі в кінці числа – завжди значущі.

0,001604 і 30,500 мають 4 і 5 значущих цифр. При розв’язуванні задач часто ставиться умова: обчислити результат з точністю до 0,1 чи 0,01. може скластись враження, що точність розрахунків визначається числом десяткових знаків після коми. Але це не так. Точність обчислення визначається числом цифр результату, що заслуговує довіри.

У виразі (1) цифра _n наближеного числа а називається вірною значущою цифрою або просто вірною, якщо виконується нерівність

або (5)

або в широкому змісті (6)

Інакше, якщо задане число (n) вірних знаків наближеного числа (а), то за абсолютну похибку можна взяти

, (7).

Якщо нерівність (5) не виконується, то цифру _n називають сумнівною.

Число вірних знаків (n) наближеного числа визначається із (5) діленням обидвох частин нерівності на а згідно (1):

_(6`)

Отже, якщо цифра _n вірна, то за відносну похибку можна взяти

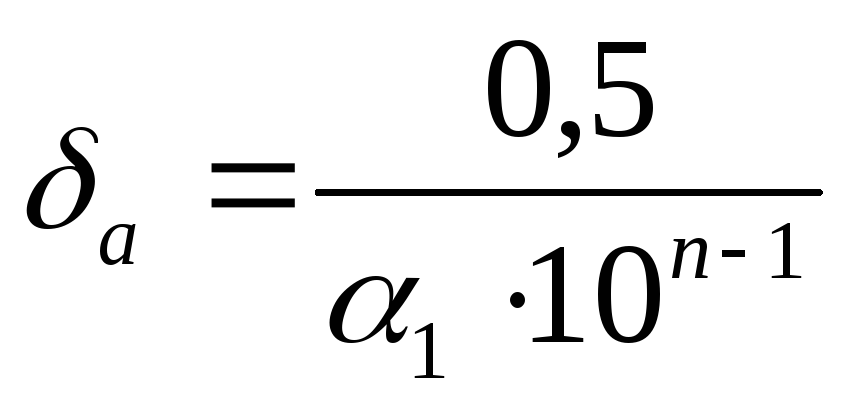(8)

Звідси, щоб цифра _n була вірною, потрібно, щоб виконувалась нерівність:

тому що в цьому випадку виконується нерівність (5) і (6’).

Кількість вірних значущих цифр в широкому змісті отримується із

Приклади

1. а = 23,10 отримане заокругленням деякого точного числа. Скільки в ньому вірних цифр? , то , n = 4.

2) а = 23,071937 містить 5 вірних цифр. Знайти абсолютну похибку.

Згідно (7) m = 1, n = 5, то

3. Абсолютна похибка числа а = 705,1978 складає Визначити, які цифри у числа а є вірними і заокруглити число, залишаючи тільки вірні цифри.

m = 2, , то (найбільше)

Отже заокруглити треба до (705).

Сумарна похибка дорівнює сумі початкової похибки та похибки заокруглення:

Отже можна записати

3. яка відносна похибка наближеного числа а = 4,176, якщо всі його цифри вірні? Згідно (8)

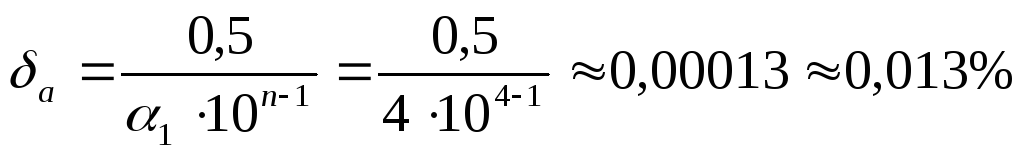
або простіше!

3. скільки вірних десяткових знаків треба взяти в , щоб похибка не перевищувала 0,1%?

а = ≈ 4.....;або

Маємо звідки

Похибки суми та різниці

- сума абсолютних похибок. Звідси випливає, що абсолютна похибка алгебраїчної суми, не повинна бути меншою за абсолютну похибку найменш точного доданку. Тому щоб не робити лишніх обчислень не потрібно зберігати лишні знаки в більш точних доданках.

При додаванні чисел різної точності поступають так:

1. виділяють число з найменшою точністю (найбільшою похибкою)

2. більш точні числа заокруглюють так, щоб зберегти в них на 1 знак більше ніж у виділеному числі (1 запасний знак)

3. додають, враховуючи всі збережені знаки

4. отриманий результат заокруглюють на 1 знак.

При n > 10 , якщо всі доданки заокруглені до

m-ого десяткового розряду

(всі цифри вірні)

Вибираємо числа з найменшою точністю: 204,4 і 144,2 їх похибка -0,05.

Решту чисел заокруглюємо:

.

Заокруглюємо результат до 374,2.

Оцінюємо точність результату:

1. вхідна початкова похибка: сума похибок 2-х найменш точних чисел та похибки заокруглення решти чисел – 0,05 · 2 + 0,005 · 7 ≈ 0,14

2. похибки заокруглення результату: 0,01

Отже А = 374,2 ± 0,15 або А = 374,2 ± 0,2.

Аналогічно поступають, якщо наближені числа є від’ємними.

Для зменшення похибки рекомендується:

1. При додаванні чи відніманні довгої послідовності чисел спочатку варто оперувати з найменшими по модулю числами.

2. Треба уникати віднімання близьких по значенню чисел та додавання чисел, що відрізняються на декілька порядків.

Відносна похибка суми знаходиться між найменшою та найбільшою відносною похибкою доданків

При відніманні відносна похибка різниці двох додатніх чисел більша за відносні похибки цих чисел, особливо, якщо ці числа близькі між собою, тобто виникає втрата точності

Нехай х = 5,125; у = 5,135; Δх = Δу = 0,0005

,

але

Отже потрібно так перетворити обчислювальну схему, щоб уникнути такої ситуації.

Наприклад,

але якщо зробити , то .

Але перетворити обчислювальну схему не завжди можливо. Тоді при відніманні близьких чисел потрібно брати їх з достатньою кількістю запасних вірних знаків.

Операційні похибки при відніманні близьких чисел зростають. Подібна ситуація характерна при розв’язуванні алгебраїчного рівняння х² + а₁х + а₀ = 0.

Якщо коефіцієнти а₁ і а₀ близькі по абсолютному значенню , то похибка коренів достатньо мала. Але при а₁ >> а₀ відносна похибка меншого по модулю кореня суттєво зростає і при а₁ > 2 · 10⁴ а₀ обчисленні за звичайною формулою корені будуть х₁ = - а₁; х₂ = 0. в цих випадках більший обчислюють за формулою , де , а знак кореня протилежний до знака а₁.

Для обчислення меншого кореня цю формулу потрібно перетворити так: домножити і поділити на множник .

Звідки х₂ = а₀ / х₁.

При розв’язуванні рівняння х² + 10000х + 8 = 0,

за звичайною формулою х₁ = -10000; х₂ = 0,

за перетвореною х₁ = -10000; х₂= -8 · 10^-4.