2.4. Литература по теме 2

1. Карасев А.И. и др. Математические методы и модели в планировании: Учебное пособие для экономических вузов/ А.И.Карасев, Н.Ш.Кремер, Т.И.Савельева: Под ред. А.И.Карасева. - М.: Экономика, 1987. - С.39-68.

2. Математическая экономика на персональном компьютере. Пер. с яп. / М.Кубонива, М.Табата, С.Табата, Ю.Хасэбэ: Под ред. М.Кубонива: Под ред. и с предисл, Е.З. Демиденко. - М.: Финансы и статистика, 1991. - С.156-215.

3. Моделирование народнохозяйственных процессов. Учебное пособие. Под ред. И.В.Котова. - Л.: Изд-во Ленинградского университета, 1990. - С.95-110.

4. Терехов Л.Л. Моделирование экономических систем: Учеб. пособие / Л.Л. Терехов; Ростовский гос. экономический ун-т «РИНХ». – Ростов н/Д, 2008. – с. 40-54.

Тема 3. Аппроксимация и экстраполяция в экономическом моделировании

3.1. Метод наименьших квадратов и его использование для нахождения аппроксимирующей функции

В экономике важными элементами анализа и прогнозирования являются аппроксимация и экстраполяция.

Аппроксимацией называют замену одних математических объектов другими, близкими к исходным. Аппроксимация функций на основе табличных данных позволяет прогнозировать числовые характеристики и качественные свойства изучаемого объекта.

Прогноз развития на будущий период с использованием аппроксимирующей функции и переносе выявленных закономерностей на будущее называют экстраполяцией.

Проблема состоит в отыскании аппроксимирующей функции. Одним из распространенных способов нахождения аппроксимирующей функции является метод наименьших квадратов.

Первоначально на основе табличных данных строится диаграмма рассеяния. Диаграмма рассеяния - это график показывающий значения пары экономических переменных для различных экономических единиц или временных периодов. Затем визуально или специальными приемами предполагается общий вид аппроксимирующей функции. Параметры такой функции определяют методом наименьших квадратов. Например, для функциональной зависимости у = а₀ + а₁х + а₂х² параметры а₀, а₁, а_2.

Рассмотрим сущность метода наименьших квадратов.

Пусть установлено, что между переменными х и у существует некоторая функциональная зависимость у = f (x), которую необходимо определить. Из статистического сборника в таблицу записаны n пар соответствующих значений этих переменных:

X	x1	x2	...	xi	...	xn-1	xn
Y	y1	y2	...	yi	...	yn-1	yn

Для решения поставленной задачи представим эти данные графически в виде диаграммы рассеяния.

y

. A_n

A_n^I

. A_i A_n-1^I

A_i^I

. A₂ . A_n-1

A₂^I y_n^I y_n

A₁^I y_i^I y_i y_n-1^I y_n-1

A₁ y₂^I y₂

y₁^I y₁

x

x₁ x₂ ... х_i ... x_n-1 x_n

В прямоугольной системе координат парам переменных ( х₁,y₁ ); (x₂,y₂); ... ; ( x_i,y_i); ... ; ( x_n-1,y_n-1 ); ( x_n,y_n ) соответствуют точки А₁, A₂, ... , A_i, ... , A_n-1, A_n.

Если между переменными величинами х и у реально существует некоторая функциональная зависимость, то точки А₁, A₂, ... , A_i, ... , A_n-1, A_n будут располагаться около плавной линии, являющейся графическим отображением этой функциональной зависимости. Задача сводится к нахождению уравнения этой линии. Это уравнение будет выражать искомую зависимость.

Однако, если исходить только из эмпирических данных, то можно подобрать много плавных кривых, которые близко подходят к построенным точкам. На вопрос о том, какой из линий отдать предпочтение, в общем случае определенного ответа дать нельзя. Также трудно решить и вопрос об уравнении этой линии.

Поступают следующим образом: вначале выбирают определенный вид уравнения. Этот вид определяется расположением построенных точек на чертеже, а также существом рассматриваемого явления.

После того, как форма уравнения выбрана, остается определить его параметры.

Например, если между переменными х и у существует линейная зависимость у = ах + b, задача сводится к определению параметров а и b.

Если процесс протекает так, что зависимость между переменными х и у выражается в виде показательной функции,

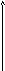
у = bа^х

то подлежат определению также два параметра.

Часто встречаются случаи, когда между х и у существует параболическая зависимость,

у = а₀ + а₁х + а₂х²

которая определяется тремя параметрами: а₀, a₁, a₂.

Иногда имеет место гиперболическая зависимость:

у = а/x + b ( 3.1.3)

В данном случае подлежат определению два параметра

и т. п.

Численные значения параметров уравнений наиболее точно определяют методом наименьших квадратов.

Вернемся к нашей диаграмме рассеяния. Предположим, что между переменными х и у существует линейная зависимость.

Может случиться, что проведенная прямая пройдет через все эмпирически найденные точки. Такой идеальный вариант не вызовет проблем в нахождении параметров a и b. Достаточно найти уравнение прямой, проходящей через две точки из имеющихся n точек.

На практике такая ситуация может встретиться лишь в виде исключения. В общем случае построенные точки лишь приблизительно лежат на этой прямой. Сама прямая отражает главным образом тенденцию изменения величин. Таким образом, пусть не все точки А₁, A₂, ... , A_i, ... , A_n-1, A_n лежат на прямой. Подстановка в уравнение у = ах + b вместо х значений x₁, x₂, ... , x_i, ... , x_n-1, x_n дает нам ординаты точек прямой у₁^I, y₂^I, ... , y_i^I, ... , y_n-1^I, y_n^I, не совпадающие с ординатами точек А₁, A₂, ... , A_i, ... , A_n-1, A_n. Поэтому разности между ними

D₁ = ах₁ + b - y₁

D₂ = ах₂ + b - y₂

......................... ( 3.1.4)

D_i = ах_i + b - y_i

.........................

D_n = ах_n + b - y_n

отличны от нуля, хотя некоторые из них могут оказаться равными нулю. Графически эти разности представляются в некотором масштабе длинами отрезков A₁A₁^I, A₂A₂^I, ... , A_nA_n^I.

Изменяя параметры а и b, мы изменяем величины отклонений D₁, D₂, ... , D_i, ... , D_n . Они могут или уменьшаться, или возрастать.

Французский математик Лежандр в 1806 году предложил взять в качестве меры отклонений сумму S квадратов этих отклонений:

S = D₁² + D₂² + ... + D_i² + ... + D_n² = (ах₁ + b - y₁ )²+(ах₂+b- y₂ )²+ + ... +

+ ( aх_i+ + b - y_i )² + ... + ( ах_n + b - y_n )²

( 3.1.5)

В качестве искомой Лежандр считал ту прямую, для которой сумма квадратов отклонений наименьшая. Отсюда и название: способ или метод наименьших квадратов.

В рассматриваемом случае сумма S является функцией переменных a и b. Условием минимума функции нескольких переменных является обращение в нуль ее частных производных по этим переменным. Выполненные преобразования позволяют получить систему нормальных уравнений:

n b + a å x_i = å y_i

b å x_i + a å x_i² = å x_i y_i

( i = 1, 2, ... , n ) ( 3.1.6)

Для отыскания параметров a и b необходимо теперь решить систему двух уравнений относительно этих двух параметров.

Если зависимость между переменными х и у выражается показательной функцией y = ba^x, то логарифмы параметров этой функции находят путем решения системы:

n ln b + ln a å x_i = å ln y_i

ln b å x_i + ln a å x_i² = å x_i ln y_i

( i = 1, 2, ... , n ) ( 3.1.7)

В тех случаях, когда между переменными х и у существует гиперболическая зависимость (у = а/x + b ), параметры а и b определяются из системы уравнений:

n b + a å 1/x_i = å y_i

b å x_i + a å 1/x_i² = å 1/x_i y_i

( i = 1, 2, ... , n ) ( 3.1.8)

Если между величинами х и у существует параболическая зависимость, то параметры а₀, a₁, a₂ этой функции определяются следующей системой уравнений:

n a₀ + a₁ å x_i + a₂ å x_i² = å y_i

a₀å x_i + a₁ å x_i² + a₂ å x_i³ = å x_i y_i

a₀å x_i² + a₁ å x_i³ + a₂ å x_i⁴ = å x_i²y_i

( i = 1, 2, ... , n ) ( 3.1.9)