10.4. Методы анализа основной тенденции (тренда) в рядах дина­мики

Важной задачей статистики при анализе рядов динамики является определение основной тенденции развития, присущей тому или иному ряду динамики. Например, за колебаниями урожайности какой-либо сельскохозяйственной культуры в отдельные годы тенденция роста (уменьшения) урожайности может не просматриваться непосредственно, и поэтому должна быть выявлена статистическими методами.

Методы анализа основной тенденции в рядах динамики разделя­ются на две основные группы:

сглаживание или механическое выравнивание отдельных членов ряда динамики с использованием фактических значений соседних уровней;

выравнивание с применением кривой, проведенной между конкрет­ными уровнями таким образом, чтобы она отображала тенденцию, при­сущую ряду и одновременно освободила его от незначительных колебаний.

Рассмотрим методы каждой группы.

Метод укрупнения интервалов. Если рассматривать уровни эко­номических показателей за короткие промежутки времени, то в силу влияния различных факторов, действующих в разных направлениях, в рядах динамики наблюдается снижение и повышение этих уровней. Это мешает видеть основную тенденцию развития изучаемого явления. В этом случае для наглядного представления тренда применяется метод укрупнения интервалов, который основан на укрупнении периодов вре­мени, к которым относятся уровни ряда. Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции и т.д.

Метод простой скользящей средней. Сглаживание ряда динами­ки с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем средний уровень из такого же числа уровней, начиная со второго, далее - начиная с третьего и т.д. Таким образом, при расчетах среднего уровня как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один и уровень вначале и добавляя один следующий. Отсюда название - скользящая средняя.

Каждое звено скользящей средней - это средней уровень за соответствующий период, который относится к середине выбранного пе­риода, если число уровней ряда динамики нечетное.

Нахождение скользящей средней по четному числу членов рядов динамики несколько сложнее, так как средняя может быть отнесена только к середине между двумя датами, находящимися в середине ин­тервала сглаживания. Например, средняя, найденная для четырех чле­нов, относится к середине между вторым и третьим, третьим и четвер­тым уровнями и так далее. Чтобы ликвидировать такой сдвиг, применя­ют так называемый способ центрирования. Центрирование заключается в нахождении средней из двух смежных скользящих средних для отнесения полученного уровня к определенной дате. При центрировании необходимо находить скользящие суммы, скользящие средние нецентрированные по этим суммам и средние из двух смежных нецентрированных скользящих средних.

Покажем расчет 5-летней и 4-летней скользящей средней на при­мере данных таблицы 10.6.

Таблица 10.6.

Сглаживание урожайности зерновых культур в хозяйстве методом скользящей средней

Годы	Центнеров с га	Скользящие пятилетние суммы	Пятилетние скользящие средние	Скользящие четырехлетние суммы	Четырехлетние скользящие средние (нецентрированные)	Четырехлетние скользящие средние центрированные
А	1	2	3	4	5	6
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16	9,5 13,7 12,1 14,0 13,2 15,6 15,4 14,0 17,6 15,4 10,9 17,5 15,0 18,5 14,2 14,9	- - - - 63,5 68,6 70,3 72,2 75,8 78,0 73,5 75,4 76,4 77,3 76,1 80,1	- - 12,5 13,7 14,1 14,4 15,2 15,6 14,7 15,1 15,3 15,5 15,2 16,0 - -	- - - 49,3 53,0 54,9 58,2 58,2 62,6 62,4 57,9 61,4 58,8 61,9 65,2 62,6	- - 12,3 13,2 13,7 14,6 14,6 15,7 15,6 14,5 15,3 14,7 15,5 16,3 15,65 -	- - 12,8 13,5 14,1 14,6 15,1 15,6 15,0 14,9 15,0 15,1 15,8 15,97 - -

Недостаток метода простой скользящей средней состоит в том, что сглаженный ряд динамики сокращается ввиду невозможности получить сглаженные уровни для начала и конца ряда. Этот недостаток устраняет­ся применением метода аналитического выравнивания для анализа ос­новной тенденции.

Аналитическое выравнивание предполагает представление уровней данного ряда динамики в виде функции времени – y = f(t).

Для отображения основной тенденции развития явлений во време­ни применяются различные функции: полиномы степени, экспоненты, логистические кривые и другие виды.

Полиномы имеют следующий вид:

полином первой степени

полином второй степени

полипом третьей степени

полином n-ой степени

Здесь - параметры полиномов, t - условное обозначе­ние времени. В статистической практике параметры полиномов невысо­кой степени иногда имеют конкретную интерпретацию характеристик динамического ряда. Так, параметр трактуется как характеристика средних условий ряда динамики, параметры - как изменения ус­корения.

В статистике выработано правило выбора степени полинома моде­ли развития, основанное на определении величин конечных разностей уровней динамических рядов. Согласно этому правилу полином первой степени (прямая) применяется как модель такого ряда динамики, у кото­рого первые разности (абсолютные приросты) постоянны, полиномы второй степени - для отражения ряда динамики с постоянными вторыми разностями (ускорениями), полиномы третьей степени - с постоянными третьими разностями и т.д.

После выбора вида уравнения необходимо определить параметры уравнения. Самый распространенный способ определения параметров уравнения - это метод наименьших квадратов.

Суть данного метода изложена в главе 9.

Согласно этому методу, для нахождения параметров полинома р-й степени необходимо решить систему так называемых нормальных урав­нений:

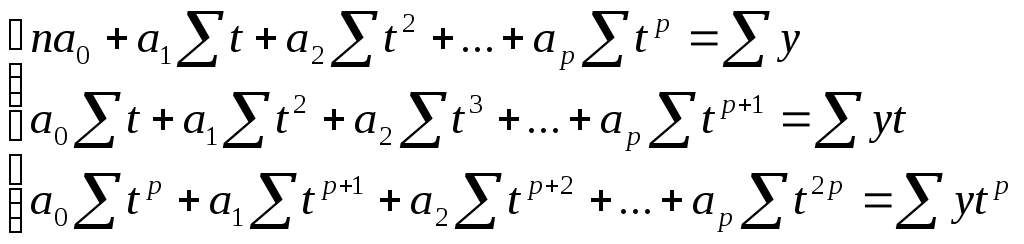(10.16.)

Система 9.16. состоящая из «р» уравнений, содержит в качестве известных величин ,, то есть суммы наблюдаемых значений уровней динамического ряда, умноженные на показатели времени в степени 0, 1, 2, …, p и неизвестных величин . Решение этой системы относительно и дает искомые значения параметров.

Системы для расчета параметров полиномов невысоких степеней намного проще. Обозначим последовательные параметры полиномов как . Тогда системы нормальных уравнений для оценивания параметров прямой примет вид:

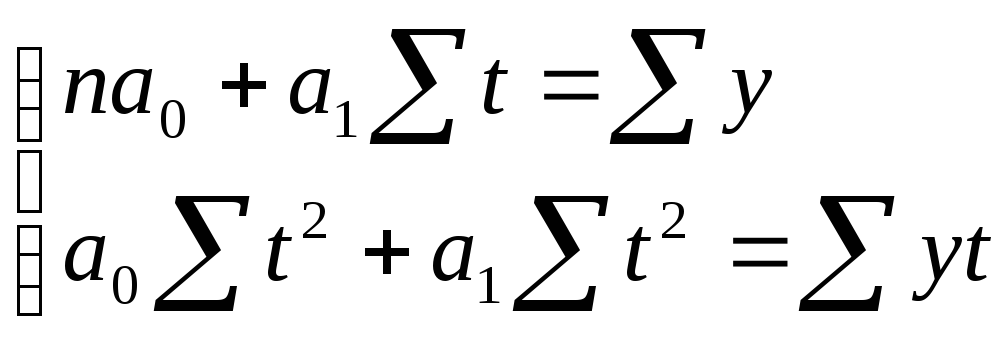(10.17.)

для параболы второго порядка :

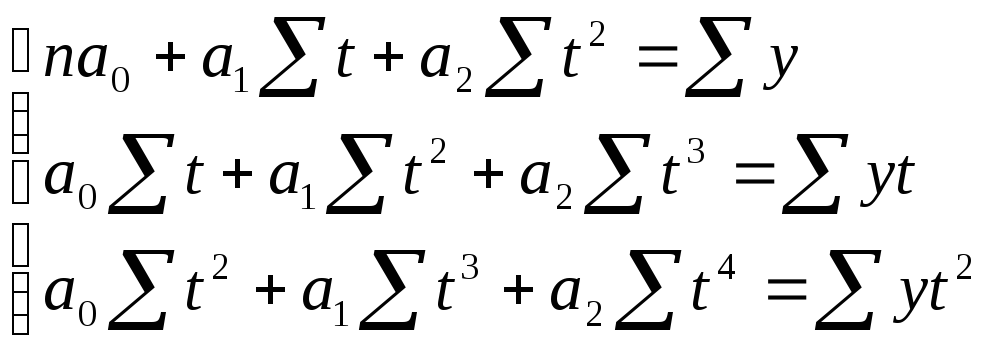(10.18.)

Решение системы (10.17.) относительно искомых параметров и дает:

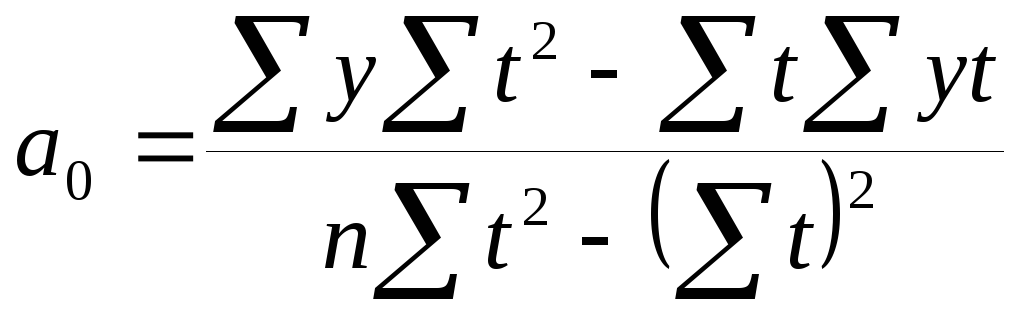
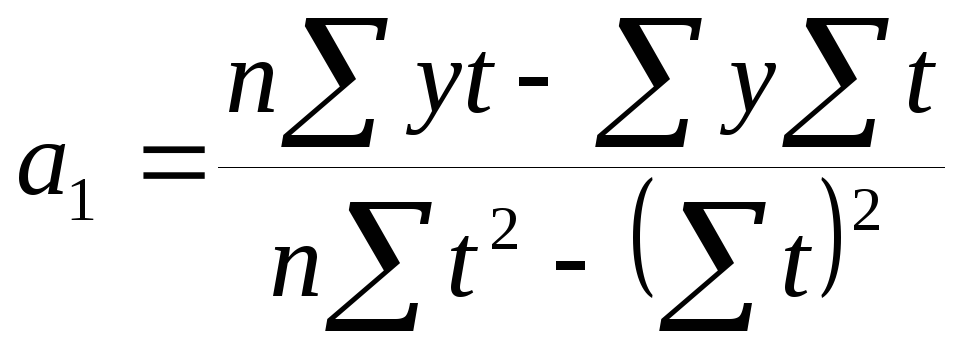
В статистической практике применяется упрощенный расчет параметров уравнений, который заключается в переносе начала координат в середину ряда динамики. В этом случае упрощаются сами нормальные уравнения, кроме того, уменьшаются абсолютные значения величин, участвующих в расчете. В самом деле, если до переноса начала координат t было равно 1, 2, 3, …, n, то после переноса t = …, -4, -3, -2, -1, 0, 1, 2, 3, 4,…, если число членов ряда нечетное. Если же число членов ряда четное , то t = …, -5, -3, -1, 1, 3, 5,… Следовательно, и все , у которых «р» - нечетное число, равны 0. Таким образом, вес члены уравнений, содержащие с такими степенями могут быть исключены. Системы нормальных уравнений теперь упрощаются для прямой:

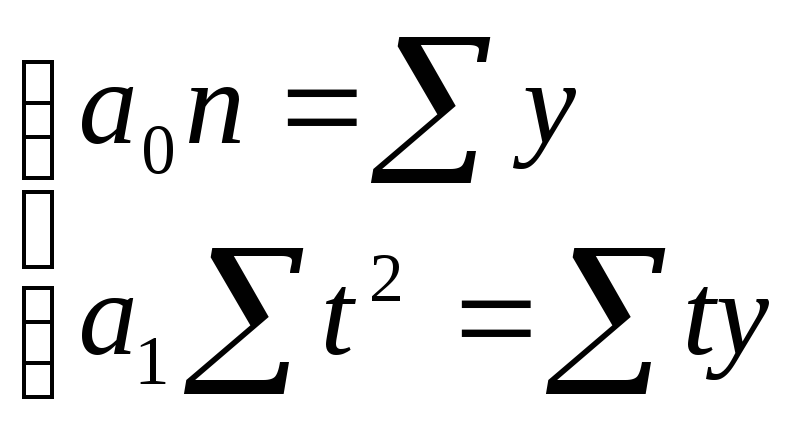(10.19.)

для параболы второго порядка:

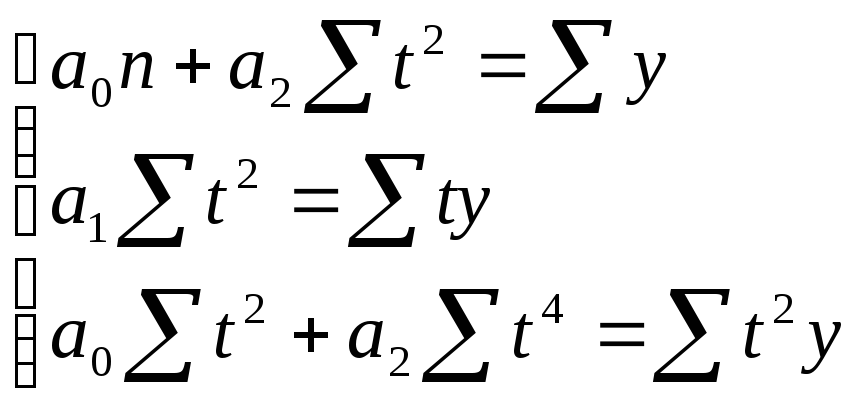(10.20.)

Решая системы (10.19.), (10.20.) относительно неизвестных параметров, получим величины параметров соответствующих полиномов.

Параметр выражает начальную скорость роста, а коэффициент - постоянную скорость изменения прироста.

При сглаживании ряда динамики по показательной кривой () для определения параметров применяется метод наименьших квадратов к логарифмам исходных данных. Так, для нахождения параметров показательной функции необходимо решить следующую систему уравнений:

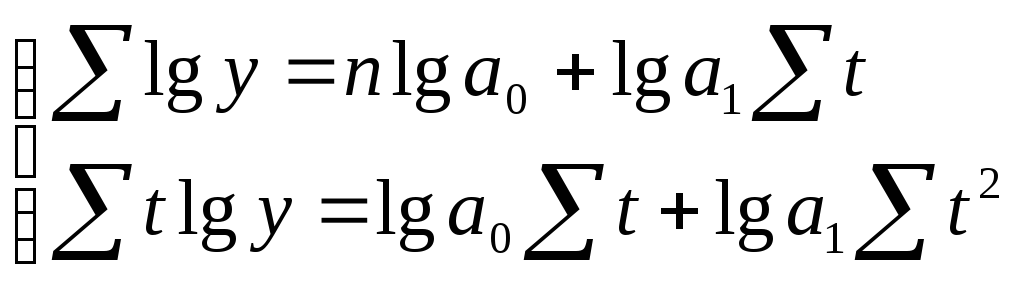(10.21.)

Если , то параметры уравнения и находим по формулам:

; .

Рассмотрим следующий пример. Необходимо определить основ­ную тенденцию ряда динамики урожайности зерновых культур в хозяй­стве за 1981-1995 гг. по следующим данным (см. табл. 10.7).

Начнем определение тенденции с самого простого полинома - уравнение прямой (10.19). Решая систему нормальных уравнений, полу­чим искомые параметры: ; , а само уравнение запишется следующим образом: , что выражает тенденцию динамики урожайности зерновых культур в 1990-2005 гг., т.е. в течение исследуе­мого периода урожайность зерновых культур в хозяйстве увеличивалась в среднем на 0,17 ц. с га в год.

Таблица 10.7.

Динамика урожайности зерновых культур в хозяйстве и определение параметров уравнения методом наименьших квадратов

Годы	Урожайность ц. с га (y)	t
1	13,7	-7	49	-95,5	13,6
2	12,1	-6	36	-72,6	13,8
3	14,0	-5	25	-70,0	13,9
4	13,2	-4	16	-52,8	14,1
5	15,6	-3	9	-46,8	14,3
6	15,4	-2	4	-30,8	14,5
7	14,0	-1	1	-14,0	14,6
8	17,6	0	0	0	14,8
9	15,4	1	1	15,4	15,0
10	10,9	2	4	21,8	15,1
11	17,5	3	9	52,5	15,3
12	15,0	4	16	60,0	15,5
13	18,5	5	25	92,5	15,7
14	14,2	6	36	85,2	15,8
15	14,9	7	49	104,3	16,0
Итого	222,0	0	280	48,8	222,0