1.2.4. Угол между двумя плоскостями

Углом φ между двумя плоскостями

A₁x+B₁y+C₁z+D₁=0

и A₂x+B₂y+C₂z+D₂=0

считается угол между их нормалями

=(A₁,B₁,C₁) и =(A₂,B₂,C₂).

Заметим, что пересекающиеся плоскости образуют два двугранных угла φ₁ и φ₂, косинусы которых отличаются лишь знаком. Достаточно вычислить острый угол между плоскостями. Тогда

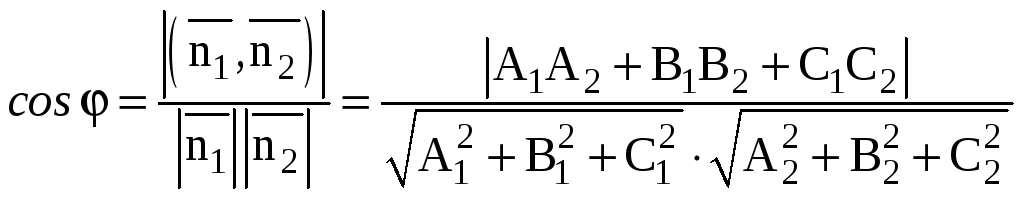. (6)

Отсюда получим условие перпендикулярности двух плоскостей:

, или

A₁A₂+B₁B₂+C₁C₂=0. (7)

Условие параллельности двух плоскостей:

где число, т.е.

. (8)

Заметим, что если верно равенство , то плоскости совпадают.

1.2.5. Расстояние от точки до плоскости

Пусть дана плоскость Ax+By+Cz+D=0 и точка M*(x*,y*,z*). Расстояние d от точки М* до плоскости вычисляют по формуле

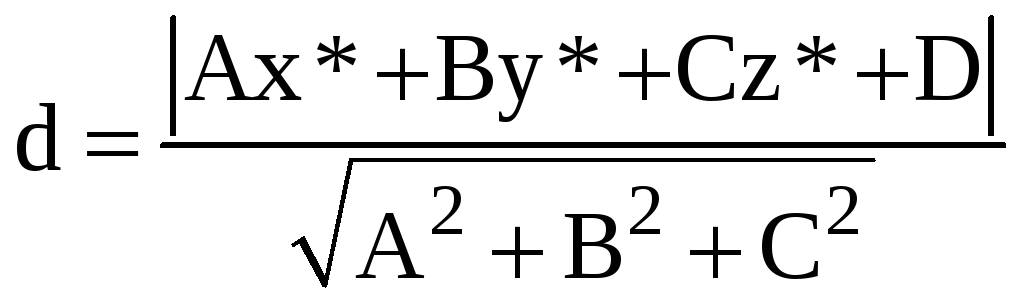. (9)

Вывод этой формулы мы опускаем.

2. Прямая в пространстве

2.1. Различные уравнения прямой

Рассмотрим прямую L в пространстве, проходящую через точку М₀(x₀,y₀,z₀) параллельно вектору =(l,m,n), который называют направляющим. Пусть М(x,y,z) – произвольная (текущая) точка на прямой. Тогда (и только тогда) векторы и коллинеарны, т.е.

=t·, (10)

где t – действительное число (параметр).

Распишем покоординатно уравнение (10):

, или

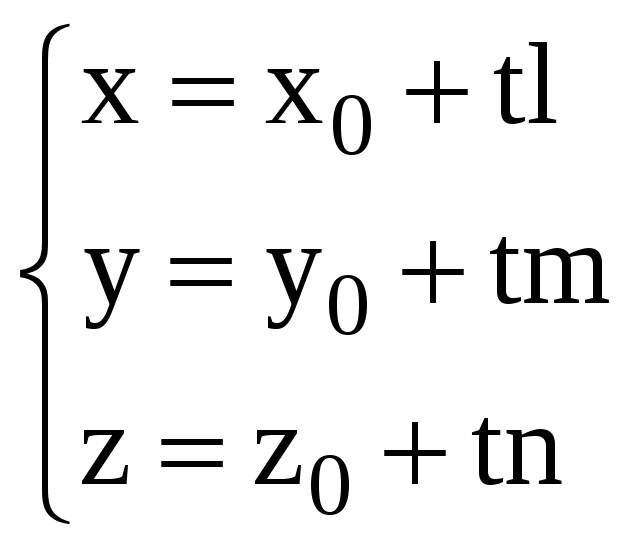(11)

Уравнения (11) называются параметрическими уравнениями прямой L в пространстве. При любом t уравнения (11) определяют некоторую точку М(x,y,z) на прямой L и, обратно, для любой точки М на прямой L однозначно определяется значение параметра t. Уравнения (11) можно трактовать как уравнения равномерного движения точки М (x,y,z) по указанной прямой, а вектор (l,m,n) – вектор скорости движения точки. При t=0 получаем «начальную» точку M₀(x₀,y₀,z₀) (рис. 4).

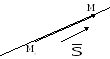
Рис. 4

Выразим параметр t из уравнений (11) и исключим его.

, или

(12)

Уравнения (12) называют каноническим уравнением прямой в пространстве. Фактически уравнения (12) выражают пропорциональность координат векторов и , т.е. условие коллинеарности этих векторов в координатной форме. Отметим, что в равенствах (12) содержится два линейных уравнения (третье следует из первых двух).

Может случиться, что какие-то координаты направляющего вектора равны нулю, этого не следует бояться. В каноническом уравнении допускается форма записи, например:

.

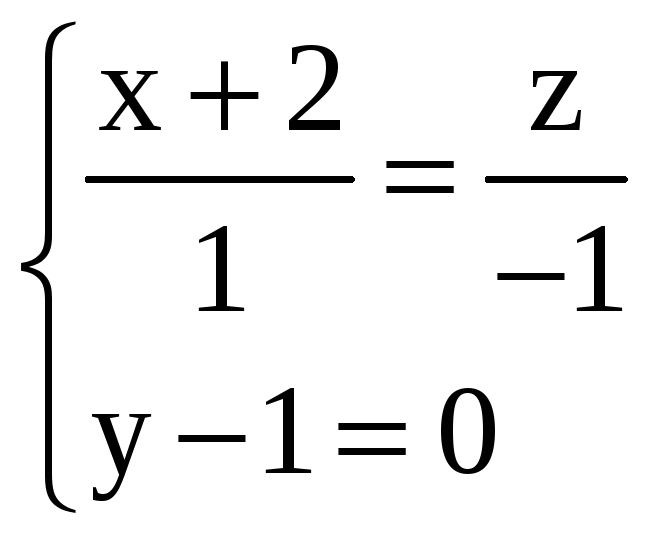Эту запись следует понимать так, что вторая координата вектора равна нулю, y – 1 = 0, или , т.е. если знаменатель в (12) равен нулю, то и числитель – ноль.