2. Понятие линейного функционала
Пусть в линейном пространстве R введена скалярная функция векторного аргумента x:
,
которая каждому
вектору x из
ставит в соответствие единственное
число
,
причем,
,
и любых чисел
.
Такую функцию
называют линейным функционалом.
Если в пространстве R
задан линейный функционал
и выбран базис e1,
e2, …, en,
то известны значения функционала на
векторах базиса
, i=1,2,…, n.
Тогда для всякого
,
где
в силу линейности функционала получим:
,
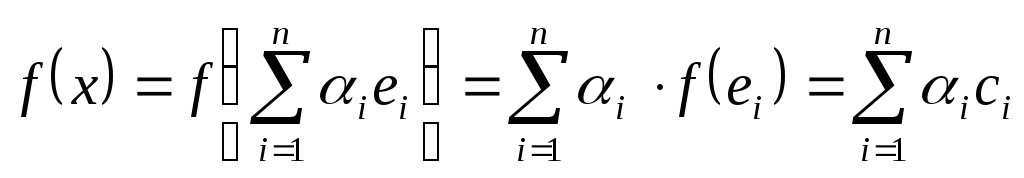(1)
где
- координаты x по базису
.
Назовем линией
уровня функционала f множество таких
точек (векторов)
,
где функция f принимает постоянное
значение:
.
Тогда, используя равенство (1), получим
(2)
Определение:
Множество точек
,
где x имеет координаты
в некотором базисе, удовлетворяющее
уравнению (2), называют плоскостью
в линейном пространстве
.
Или уравнение
,
где с1, с2,
…сn – заданные
числа, а α1, α2, …,αn
– координаты произвольного вектора
,
называют плоскостью в аффинном
пространстве.
3. Гиперплоскость в пространстве Rn
Рассмотрим в
качестве примера арифметическое линейное
пространство
,
и введенное в
скалярное произведение векторов:
,
где
и
,
.
Пусть в
задан некоторый ненулевой вектор
,
тогда функция, заданная для всякого
следующим образом
,
очевидно является линейным функционалом.
Рассмотрим в
множество векторов
,
ортогональных вектору а.
Определение:
Уравнение
,
или
(3)
определяет
гиперплоскость в
,
проходящую через начало координат
(нулевая гиперплоскость). Легко проверить,
что совокупность точек
,
лежащих на гиперплоскости (3), является
подпространством пространства
.
Множество
также называют
гиперплоскостью в
,
но это множество уже не образует
подпространства, хотя бы потому, что не
содержит 0-вектора.
В этом случае
гиперплоскость является сдвигом
нулевой гиперплоскости
Вообще, если V
- подпространство пространства
,
x0 – фиксированный вектор, не
принадлежащий V, тогда
совокупность W всех таких
векторов x, что
,
где y пробегает все подпространство V,
называют сдвигом подпространства V
на вектор x0.
В этом многомерном случае легко видна аналогия с уравнением плоскости в трехмерном пространстве
,
(4)
где точка М с координатами (x, y, z) лежит на плоскости, а вектор
- вектор нормали
к плоскости (4).
4. Уравнение прямой в произвольном линейном пространстве Rn
Аналогично уравнению
прямой в R3 можно ввести понятие
прямой линии в n–мерном линейном
пространстве
.
Пусть в
выбрана фиксированная точка x0 и
фиксированный ненулевой вектор
,
а параметр t принимает произвольные
числовые значения. Тогда совокупность
точек
,
где
(5)
назовем прямой линией в линейном (аффинном) пространстве Rn.
Если выбран базис
в
и заданы координаты
и
то параметрическое уравнение прямой
будет иметь вид:
.
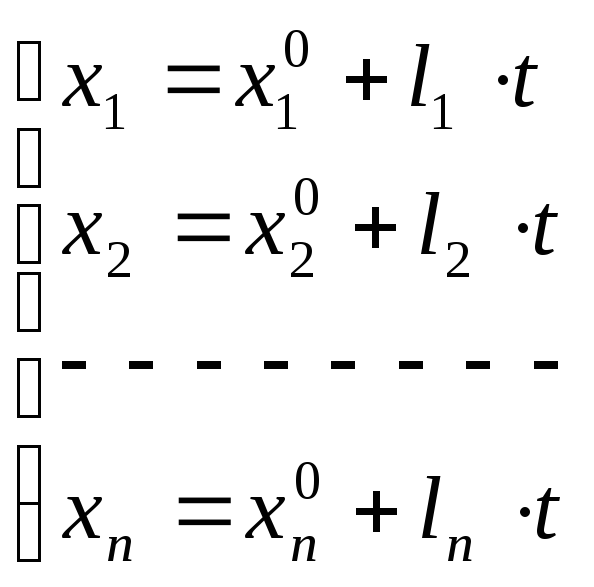(5’)
Уравнение
(5), или (5') задает прямую, проходящую
через точку x0
с направляющим вектором
.