Вероятностные оценки погрешности результата измерений на основании ряда наблюдений

Измерения физических величин могут быть произведены с раз­личной точностью. Иногда оказывается вполне достаточным знание приближенного значения измеряемой величины, полученного, например, по показанию прибора невысокой точности. Однако во многих научных исследованиях при измерениях преследуется цель ппоеделения измеряемой величины с высокой точностью, для чего необходимо дать оценку погрешности результата измерения или установить границы искомого параметра. Эту оценку можно получить на основании обработки результатов наблюдений.

Целью обработки результатов наблюдений является установле­ние действительного значения измеряемой величины, которое может быть принято вместо истинного значения измеряемой величины, и степени близости действительного значения к истинному.

Действительное значение, как результат обработки отдельных наблюдений, содержащих случайные погрешности, само по себе неизбежно содержит случайную погрешность. Поэтому степень близости действительного и истинного значения измеряемой вели­чины нужно оценивать с позиций теории вероятностей. Такой оценкой является доверительный интервал.

Доверительный интервал и доверительная вероятность. Если известен закон распределения погрешностей, можно определить вероятность появления погрешности δ, не выходящей за некоторые принятые границы. Этот интервал называют доверительным интер­валом, а характеризующую его вероятность - доверительной ве­роятностью. В практике измерений применяют различные значе­ния доверительной вероятности, например: 0,90; 0,95; 0,98; 0,99; 0,9973 и 0,999. Доверительный интервал и доверительную вероят­ность выбирают в зависимости от конкретных условий измерений. Так, например, при нормальном законе распределения случайных погрешностей со средним квадратическим отклонением σ часто пользуются доверительным интервалом от +3σ до -3σ, для кото­рого доверительная вероятность равна 0,9973. Такая доверитель­ная вероятность означает, что в среднем из 370 случайных погреш­ностей только одна погрешность по абсолютному значению будет больше Зσ. Так как на практике число отдельных измерений редко превышает несколько десятков, появление даже одной случайной погрешности, большей, чем 3σ, будет маловероятным событием, наличие же двух подобных погрешностей почти невозможно. Это позволяет с достаточным основанием утверждать, что все возмож­ные случайные погрешности измерения, распределенные по нормаль­ному закону, практически не превышают по абсолютному значе­нию 3σ (правило «трех сигм»).

Доверительный интервал (ГОСТ 8.011-72) является одной из основных форм выражения точности измерений. Одну из форм представления результата измерения этот ГОСТ устанавливает в следующем виде:

где А - результат измерения (действительное значение) в едини­цах измеряемой величины; Δ, Δ_н, Δ_в - соответственно погрешность измерения с нижней и верхней ее границами в тех же единицах⁸, Р - установленная вероятность, с которой погрешность измере­ния находится в этих границах.

ГОСТ 8.011-72 допускает и другие формы представления ре­зультата измерения, однако любая из этих форм должна содержать необходимые данные, на основании которых может быть определен доверительный интервал для погрешности результата измерения.

В общем случае доверительный интервал может быть установ­лен, если известен вид закона распределения погрешности и основ­ные характеристики этого закона.

Оценка погрешности результата измерений. Для правильной оценки результата измерений и его погрешности необходимо произ­водить обработку результатов отдельных наблюдений ряда в сле­дующем порядке.

1. Оценить и исключить систематическую погрешность из каж дого отдельного результата ряда наблюдений, получив таким обра­зом исправленный ряд наблюдений, не содержащий систематических погрешностей.

2. Для исправленного ряда наблюдений оценить основные его характеристики (математическое ожидание и среднее квадратиче­ское отклонение⁹).

3. Найти результат измерения (действительное значение изме­ряемой величины) и оценку среднего квадратического отклонения погрешности результата измерения.

4. Определить вид закона распределения оценки погрешности результата измерения и найти доверительный интервал для этой погрешности.

Рассмотрим наиболее характерные случаи обработки результа­тов наблюдений при различных видах измерений.

Прямые измерения. Предположим, что при многократном изме­рении интересующей нас величины получили п отдельных резуль­татов наблюдений. Исключив систематическую погрешность из каждого наблюдения, получаем исправленный ряд значений а₁, a₂,…a_n, математическим ожиданием которого является истинное значение измеряемой величины A_и. За действительное значе­ние измеряемой величины принимаем среднее арифметическое, определяемое по формуле (2.3), в которой a_i - значение исправ­ленного ряда.

Из теории вероятностей известно, что дисперсия среднего ариф­метического в n раз меньше дисперсии ряда наблюдений, по кото­рому оно получено. Следовательно,

(2.5)

где σ² - дисперсия исправленного ряда наблюдений; а²_А - диспер­сия среднего арифметического этого ряда.

Если дисперсия ряда неизвестна, то ее нужно оценить по фор­муле (2.4), в которой ρ_i - остаточные погрешности исправленного ряда наблюдений.

В этом случае за оценку дисперсии действительного значения нужно принять величину

(2.6)

Для нахождения доверительного интервала необходимо найти закон распределения для величины

(2.7)

при известной дисперсии или для величины

(2.8)

при неизвестной дисперсии.

В теории вероятностей доказано, что для нормального закона распределения случайной погрешности ряда наблюдений выраже­ние (2.7) есть случайная величина z, распределенная по нормаль­ному закону с математическим ожиданием, равным нулю, и диспер­сией, равной единице, а выражение (2.8) - случайная величина t, распределенная по закону Стьюдента¹⁰. Для z и t существуют таб­лицы, по которым можно найти значения z_р и t_p (f), определяющие с доверительной вероятностью Р границы доверительного интер­вала для величин z и t соответственно. Число f называется числом степеней свободы; для рассматриваемого случая f = n - 1.

Чем больше число измерений в ряду наблюдений, тем ближе оценка S_A совпадает с действительным средним квадратическим отклонением σ_А. Следовательно, с увеличением числа наблюдений закон распределения Стьюдента приближается к нормальному закону. Практически при n > 30 z_p ≈ t_p (f).

Зная z_p или t_p (f), на основании (2.7) и (2.8) с учетом (2.5) и (2.6), результат измерения с доверительной вероятностью Р можно записать в виде

(2.9)

при известной дисперсии или в виде

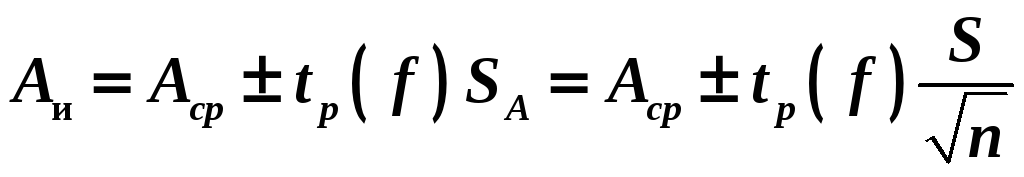(2.10)

при неизвестной дисперсии.

На практике часто встречается случай однократного измерения, когда измеряемая величина оценивается по результату одного наб­людения. Этот случай можно рассматривать как частный случай многократных наблюдений (при п = 1). Тогда выражения (2.9) и (2.10) примут вид:

(2.11)

и

(2.12)

Здесь за действительное значение A измеряемой величины сле­дует принять результат однократного измерения, из которого исклю­чена систематическая погрешность. Нужно иметь в виду, что по однократному измерению нельзя определить σ (или S). Поэтому для того чтобы можно было записать результат измерения в виде (2.11), среднее квадратическое отклонение σ нужно знать на осно­вании предварительных измерений или из технической докумен­тации на применяемое средство измерений. Если вместо о известна его оценка S, найденная по некоторому числу предварительных измерений, то для определения t_p (f) в выражении (2.12) число степеней свободы f нужно взять, равным этому числу предвари­тельных измерений минус единица.

Сравнение выражений (2.9), (2.10) и (2.11), (2.12) показывает, что увеличение числа наблюдений позволяет получить более точную оценку истинного значения измеряемой величины.

Косвенные измерения. Допустим, что измеряемая величина у является функцией аргументов а, b, с,…, измеряемых прямыми измерениями, т. е. у = F (a, b, c,...). Проведя обработку ряда наблюдений для каждого аргумента методом, изложенным для .прямых измерений, можно найти действительные значения аргу­ментов А, В, С, ... и их средние квадратические отклонения А, B, C, ... или их оценки S_A, S_B, S_C, …

Действительное значение измеряемой величины Y можно найти как

(2.13)

Дисперсия величины Y при условии независимости прямых из­мерений аргументов а, b, с, ... вычисляется по формуле

(2.14)

Следует обратить внимание, что в выражении (2.14) частные про­изводные функции по каждому аргументу вычисляются в точке, где аргументы принимают значения А,В,С,...

Если вместо дисперсий известны их оценки S²_A, S²_B, S²_C, … то оценку дисперсии величины Y нужно определить по формуле, аналогичной (2.14), т. е.

(2.15)

Для того чтобы найти доверительный интервал погрешности результата косвенного измерения, нужно определить закон распределения величин¹¹ 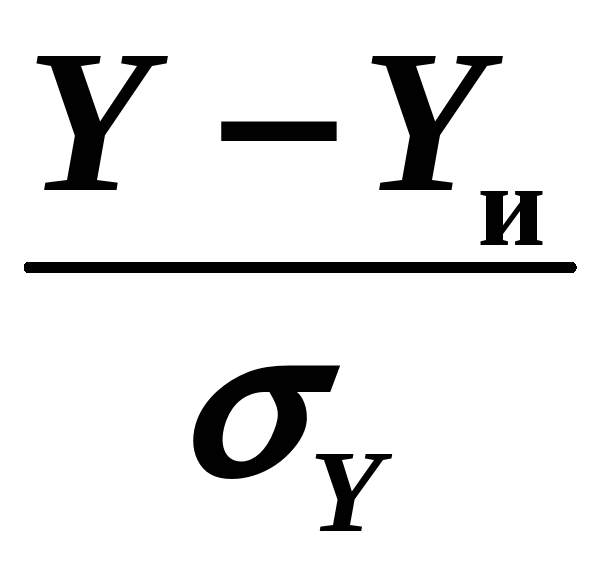или .

Совместные измерения. Целью совместных измерений является установление функциональной зависимости между величинами, .например зависимости сопротивления от температуры. Отыскивая зависимость между величинами a и b, необходимо устанавливать и измерять различные значения величины а и одновременно изме­рять соответствующие значения величины b. Таким образом, можно лолучить координаты исследуемой зависимости a₁, b₁; a₂, b₂; …; a_n, b_n. Так как результаты измерения этих значений содержат погрешности, то полученные координаты не будут принадлежать истинной исследуемой зависимости. Исключив систематическую погрешность из каждого результата измерения, можно уточнить эти координаты, но и уточненные координаты все-таки будут рас­сеиваться относительно истинной зависимости из-за случайных погрешностей.

Степень рассеивания, как известно, характеризуется диспер­сией. Правильной зависимостью, построенной по полученным координатным точкам, следует считать такую зависимость, при которой дисперсия координатных точек относительно этой зависи­мости будет минимальной. Для оценки дисперсии нужно вычис­лить сумму квадратов отклонений координатных точек от истин­ной зависимости. Минимальной дисперсии будет соответствовать минимальное значение суммы квадратов этих отклонений. Поэтому метод, с помощью которого отыскивается истинная зависимость, называется методом наименьших квадратов.

Рассмотрим применение этого метода на примере линейной зави­симости между а и b. Предположим, нам известно, что зависимость между а и b должна описываться уравнением

(2.16)

Результаты эксперимента после исключения систематических Погрешностей дают нам координаты исследуемой зависимости a₁, b₁; …; a_n, b_n. Необходимо решить, как провести прямую линию, наилучшим образом согласующуюся с полученными координа­тами. Иными словами, зная координаты, полученные эксперимен­тально, и вид функции, нужно определить коэффициенты α и β в уравнении (2.16).

В соответствии с уравнением (2.16), если величина b прини­мает значение b_i, то значение а должно быть равно φ(α, β, b_i), а эксперимент дает значение a_i. Следовательно, экспериментальная точка отклоняется от истинной точки на значение a_i - φ(α, β, b_i). Сумму квадратов отклонений экспериментальных точек от истин­ной зависимости можно найти по выражению

(2.17)

Найдем значения коэффициентов α и β обращающие выраже­ние (2.17) в минимум. Для этого продифференцируем это выражение по α и β и приравняем производные нулю:

(2.18)

Систему уравнений (2.18) с учетом (2.16) легко привести к виду

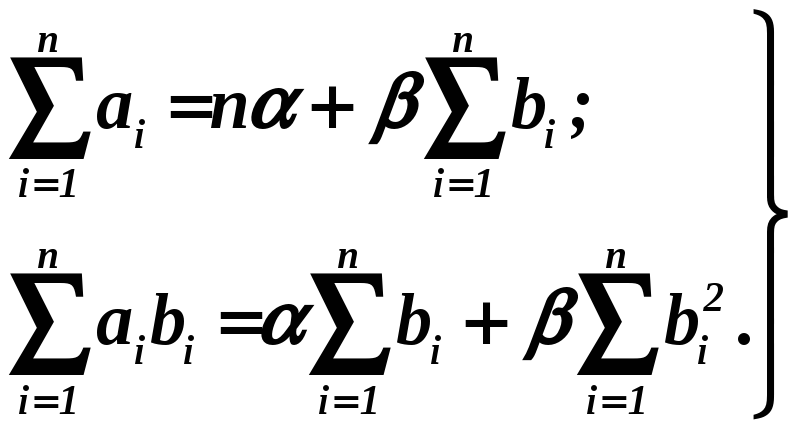(2.19)

Решая систему уравнений (2.19), получим выражение для коэф­фициента β:

(2.20)

а зная β, находим выражение для α:

(2.21)

Методами теории вероятностей можно установить точность полученных таким образом значений коэффициентов α и β.