1.2.1. Способы задания бинарных отношений

Для задания бинарных отношений могут быть использованы любые способы задания множеств. Отношения, определенные на конечных множествах обычно задаются:

1. Списком (перечислением) пар, для которых это отношение выполняется. Например,

2. Матрицей – бинарному отношению , где , соответствует квадратная матрица порядка в которой элемент , стоящий на пересечении i–й строки и j–ого столбца, равен 1, если между 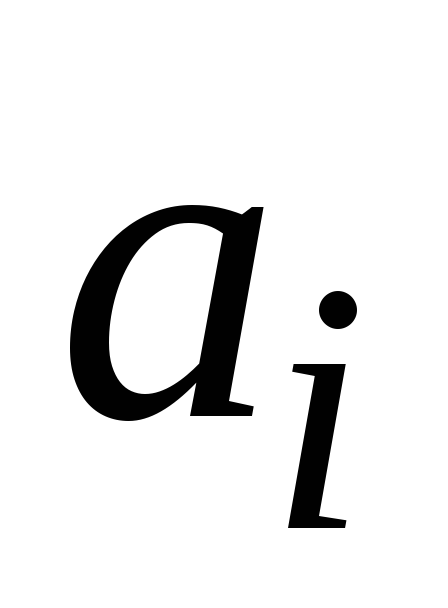и имеет место отношение , или 0, если нет: .

3. Направленным графом, то есть структурой, состоящей из вершин и дуг (направленных ребер). Элементы множеств отображаются в виде вершин графа, а отношения – в виде дуг, соединяющих эти вершины.

Пример. Пусть . Задать в явном виде (списком), описанием характеристических свойств и матрицей и графом отношение , если означает – «быть строго меньше».

1. С использованием распознающей процедуры можно записать .

2. Списком .

3. Матрица и граф данного отношения имеют вид:

Пример. Для того же самого множества М={1,2,3,4,5,6} составить матрицы отношений , если

R1 – быть делителем,

R2 – иметь один и тот же остаток от деления на 3.

Матрицы имеют вид:

, .

1.2.2. Свойства бинарных отношений

Пусть – отношение на множестве , . Тогда:

1. – рефлексивно, если имеет место 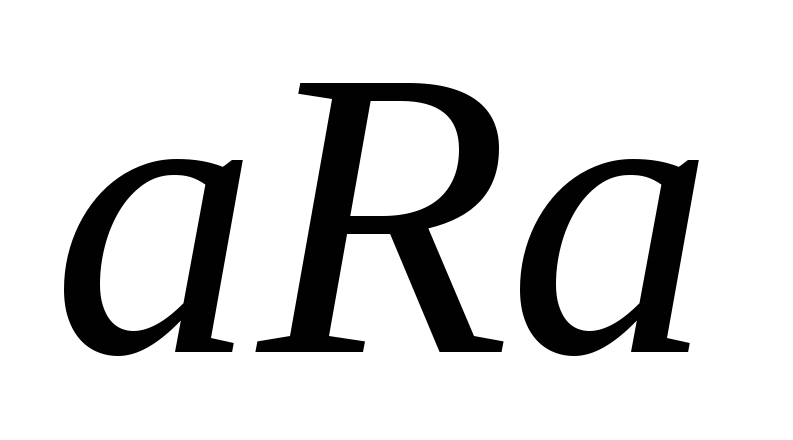для любого . Например, отношение, рефлексивно.

2. – антирефлексивно, если ни для какого не выполняется . Например, отношение “быть сыном”.

3. – симметрично, если влечет . Например, отношение «жить в одном городе» – симметрично.

4. – антисимметрично, если 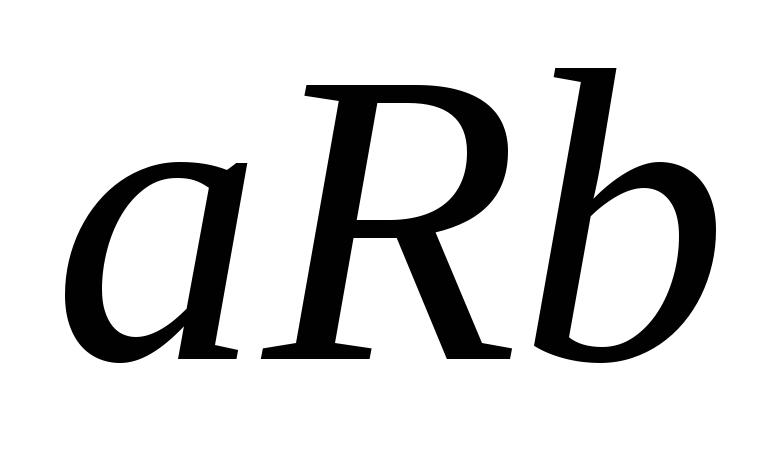и 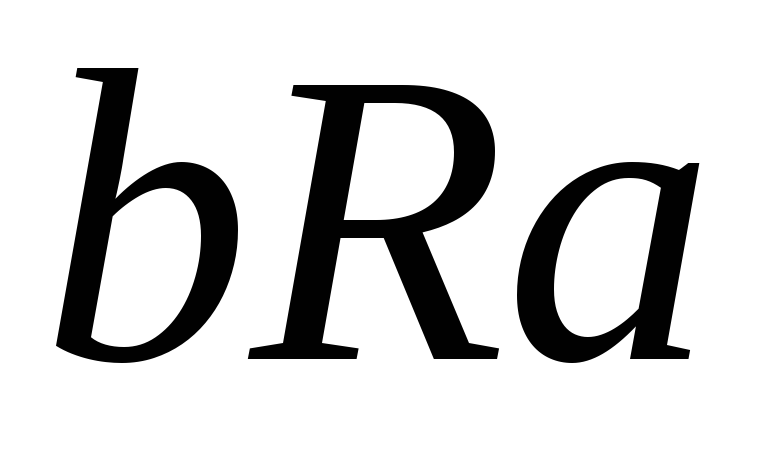влекут 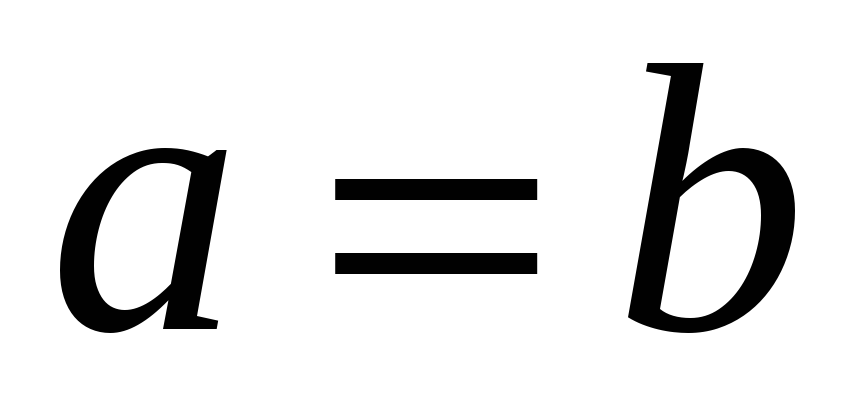, т.е. ни для каких различающихся элементов и 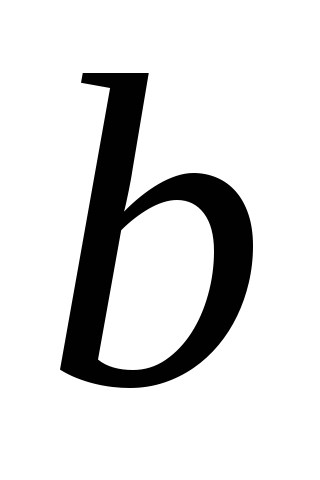() не выполняется одновременно и . Например, отношение “быть начальником” антисимметрично.

5. – транзитивно, если и влекут . Например, отношение «быть моложе» транзитивно.

Пример. Каковы свойства отношения «Быть не больше» (), заданного на множестве натуральных чисел N?

Рефлексивно, так как для всех .

Антисимметрично, поскольку, если и , то .

Транзитивно, так как, если и , то .

Пример. Пусть и пусть определено в виде

. Каковы свойства отношения?

не является рефлексивным, т. к. , но .

не является симметричным, поскольку , но .

не является антисимметричным, поскольку и , но .

не является транзитивным, т.к. и , но .

1.2.3. Эквивалентность и порядок

Рассматриваемые ниже отношения представляют собой формально определенные типы отношений, отличающиеся фиксированным набором свойств.

Отношением эквивалентности (или просто эквивалентностью) называют бинарное отношение на множестве, если оно рефлексивно, симметрично, транзитивно. Например, отношение «жить в одном городе» на множестве людей – эквивалентность.

Отношение эквивалентности имеет важную особенность: эквивалентность разбивает множество , на котором оно задано, на непересекающиеся подмножества так, что элементы одного и того же подмножества находятся в отношении , а между элементами разных подмножеств оно отсутствует. В этом случае говорят, что отношение задает разбиение на множестве , или систему классов эквивалентности по отношению . Мощность этой системы называется индексом разбиения.

В то же время, любое разбиение множества на классы определяет некоторое отношение эквивалентности, а именно отношение «входить в один и тот же класс данного разбиения».

Это очень важное утверждение, так как дает основание строго определить свойства рефлексивности, симметричности и транзитивности некоторых отношений. Например, что сказать об отношении, заданном нуль–графом с петлями? Таким будет отношение «жить в одном городе» на множестве, где все люди живут в разных городах. Сам факт, что данное отношение разбивает множество на классы эквивалентности говорит о том, что оно симметрично и транзитивно, хотя граф не имеет ни одного ребра.

Пример.

Пусть множество – это набор разноцветных шаров, а отношение задается условием тогда и только тогда, когда а и b имеют одинаковый цвет. Поскольку – отношение эквивалентности, каждый класс эквивалентности будет состоять из шаров, имеющих одинаковый цвет.

Замечание. Из того, что отношение «жить в одном городе» разбивает множество людей на непересекающиеся подмножества, т.е. является эквивалентностью, следует, что с точки зрения математики вполне естественно утверждение «Иванов живет в одном городе с самим собой», как условие рефлексивности данного отношения. Такие утверждения, не вызывающие сомнения при работе с числами, например , выглядят непривычно, если элементами множеств являются люди.

Отношением нестрогого порядка (или нестрогим порядком) называют бинарное отношение на множестве, если оно рефлексивно, антисимметрично, транзитивно, и отношением строгого порядка (строгим порядком), если оно антирефлексивно, антисимметрично, транзитивно. Оба эти отношения называются отношениями порядка.

Например, отношение «быть не старше» на множестве людей, «быть не больше» на множестве натуральных чисел» – нестрогий порядок. Отношения «быть моложе», «быть прямым потомком» на множестве людей – строгий порядок.

Элементы сравнимы по отношению порядка на , если выполняется или .

Множество , на котором задано отношение порядка , может быть:

• полностью упорядоченным множеством, если любые два элемента этого множества сравнимы по отношению порядка ,

• частично упорядоченным множеством, если сравнимы лишь некоторые элементы этого множества.

Пример.

Отношения полного порядка на множестве людей – быть моложе, быть выше и т.д.

Отношение частичного порядка на множестве людей – быть начальником.