3.1.2. Способы задания графов
Наиболее простым и естественным способом задания графа является графический. Однако, таким образом можно задать только небольшие графы. К тому же он неудобен для автоматизированной обработки и передачи графической информации. Рассмотрим другие способы, используемые в теории графов.
В
общем виде задать граф – значит описать
множества его вершин и ребер, а также
отношение инцидентности. Для описания
вершин и ребер их достаточно занумеровать.
Пусть
– вершины графа
;
– ребра. Отношение инцидентности может
быть задано следующими способами.
Матрицей
инцидентности
размера
.
По вертикали и горизонтали указываются
вершины и ребра соответственно, а на
пересечении
–ой
вершины и
–ого
ребра в случае неориентированного графа
проставляется 1, если они инцидентны, и
0 – в противоположном случае, т.е.
,
а в случае орграфа: – -1, если вершина является началом дуги, 1 – если вершина является концом дуги и 0 – если вершины не инцидентны. Если некоторая вершина является для ребра и началом и концом (т.е. ребро – петля), проставляется любое другое число, например 2.
Списком
ребер графа,
представленным двумя столбцами: в левом
перечисляются все ребра
,
в правом – инцидентные им вершины
.
Для н–графа порядок вершин произволен,
для орграфа первым стоит номер начала
дуги. При наличии в графе изолированных
вершин они помещаются в конец списка.
Матрицей
смежности
– квадратной матрицей размера
.
По вертикали и горизонтали перечисляются
все вершины, а на пересечении
–й
и
–ой
вершин в случае н–графа проставляется
число
,
равное числу ребер, соединяющих эти
вершины. Для орграфа
равно числу ребер с началом в
–ой
вершине и концом в
–ой
вершине.
Пример. Задать различными способами графы, представленные на рис.3.4.
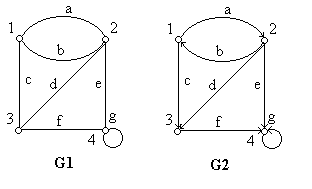
Рис. 3.4.
Матрицы инциденции графов имеют вид:
|
|
a |
b |
c |
d |
e |
f |
g |
|
1 |
1 |
1 |
1 |
|
|
|
|
|
2 |
1 |
1 |
|
1 |
1 |
|
|
|
3 |
|
|
1 |
1 |
|
1 |
|
|
4 |
|
|
|
|
1 |
1 |
1 |
|
|
a |
b |
c |
d |
e |
f |
g |
|
1 |
-1 |
1 |
-1 |
|
|
|
|
|
2 |
1 |
-1 |
|
-1 |
-1 |
|
|
|
3 |
|
|
1 |
1 |
|
-1 |
|
|
4 |
|
|
|
|
1 |
1 |
2 |
Список ребер является более компактным описанием графа:
|
Ребро |
Вершины |
|
a |
1 2 |
|
b |
2 1 |
|
c |
1 3 |
|
d |
2 3 |
|
e |
2 4 |
|
f |
3 4 |
|
g |
4 4 |
Следующие
таблицы представляют матрицы смежности
графов
и
:
|
|
1 |
2 |
3 |
4 |
|
|
1 |
2 |
3 |
4 |
|
1 |
|
2 |
1 |
|
|
1 |
|
1 |
1 |
|
|
2 |
2 |
|
1 |
1 |
|
2 |
1 |
|
1 |
1 |
|
3 |
1 |
1 |
|
1 |
|
3 |
|
|
|
1 |
|
4 |
|
1 |
1 |
1 |
|
4 |
|
|
|
1 |
