2.5.4. Префиксная нормальная форма

. (Может быть не нужно)

Формулы называются эквивалентными, если при любых подстановках констант они принимают одинаковые значения. В частности, все тождественно истинные (или тождественно ложные) формулы эквивалентны.

Множество истинных формул логики предикатов входит в любую теорию, и, следовательно, его исследование является важнейшей целью логики предикатов. В этом исследовании прежде всего возникают две проблемы: получение истинных формул и проверка формулы на истинность. Если вспомнить классификацию способов задания множеств, то первая проблема – это проблема построения порождающей процедуры, а вторая – проблема разрешающей процедуры для множества истинных формул . Те же проблемы встают и в логике высказываний.

Но там есть стандартная разрешающая процедура: вычисление формул на наборах значений переменных. С ее помощью порождающую процедуру для множества тождественно истинных высказываний можно реализовать следующим образом: строим последовательно все формулы, вычисляем каждую из них на всех наборах и включаем в только те, которые истинны на всех наборах. Аналогичная процедура в логике предикатов сталкивается с большими трудностями, связанными с тем, что предметные переменные имеют в общем случае бесконечные области определения. Поэтому прямой перебор всех значений, как правило, невозможен. Приходится использовать приемы, базирующиеся на эквивалентных соотношениях. Приведем в качестве примера некоторые из них:

,

.

Можно показать, что

,

.

Если же и в этих выражениях поменять местами, то получатся соотношения верные лишь в одну сторону:

, (2.3)

. (2.4)

Для (2.4) требуется, чтобы в левой части хотя бы один предикат выполнялся для всех х, для правой же достаточно, чтобы один предикат был истинен там, где другой ложен.

В таких случаях говорят, что левая часть более сильное утверждение, чем правая, поскольку она требует для своей истинности выполнения более жестких условий, чем правая. Так в (2.3) в левой части требуется, чтобы и были истинны для одного и того же , тогда как в правой части и могут быть истинны при различных и . Пример, когда (2.3) в обратную сторону неверно: – « – четное число», – « – нечетное число».

Приведем без доказательства еще несколько соотношений:

.

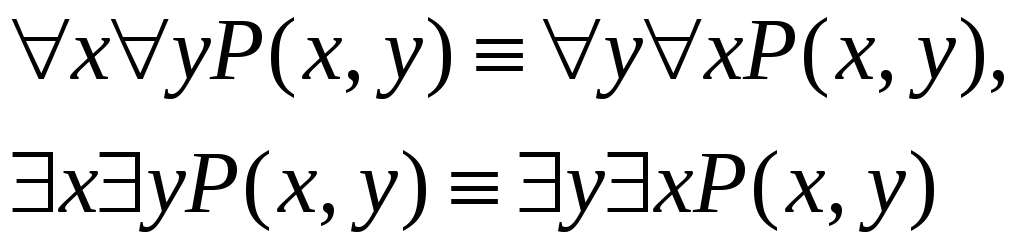
Эти соотношения означают, что формулу, не содержащую , можно выносить за область действия квантора, связывающего .

Как и в логике высказываний, в логике предикатов существуют эквивалентные нормальные формы представления любых предикатных формул.

Определение. Префиксной нормальной формой (ПНФ) называется формула имеющая вид:

где – кванторы, – формула, не имеющая кванторов, с операциями . В логике предикатов для любой формулы существует эквивалентная ей ПНФ.

Процедура получения ПНФ включает следующие этапы:

1. Используя формулы

заменить операции {, } на {,,}.

2. Воспользовавшись выражениями замены кванторов, а также правилом двойного отрицания и правилом де Моргана

представить предикатную формулу таким образом, чтобы символы отрицания были расположены непосредственно перед (над) символами предикатов.

3. Для формул, содержащих подформулы вида

,

ввести новые переменные.

4. С помощью формул эквивалентных преобразований получить формулы в виде ПНФ.

Пример. Привести к ПНФ следующую предикатную формулу: .

Применив правило де Моргана, получим:

.

Далее, перенесем кванторы через отрицание:

.

Так как квантор общности не дистрибутивен относительно дизъюнкции, поменяем в каком-либо предикате, например во втором, переменную на новую переменную :

.

Воспользовавшись дважды эквивалентным отношением выноса функции не зависящей от х из под кванторов , получим:

.

Поскольку квантор существования дистрибутивен относительно дизъюнкции, окончательно получим:

.