2.5.2. Кванторы

Пусть – предикат, определенный на . Высказывание «для всех из истинно» обозначается . Множество не входит в обозначение и должно быть ясно из контекста. Знак называется квантором общности.

Высказывание «существует такой из , что истинно» обозначается . Знак называется квантором существования. Переход от к или называется связыванием переменной , а также навешиванием квантора на переменную (или на предикат ). Переменная, на которую навешан квантор, называется связанной, в противном случае – свободной.

Смысл связанных и свободных переменных в предикатных выражениях различен. Свободная переменная – это обычная переменная, которая может принимать различные значения из ; выражение – переменное высказывание, зависящее от значения . Выражение не зависит от переменной и при фиксированных и имеет вполне определенное значение. Переменные, являющиеся по существу связанными, встречаются не только в логике. Например, в выражениях или переменная связана. При фиксированной первое выражение равно определенному числу, а второе, функции от и .

Навешивать кванторы можно и на многоместные предикаты и вообще на любые выражения, которые при этом заключаются в скобки. Выражение, на которое навешивается квантор или , называется областью действия квантора. Навешивание квантора на многоместный предикат уменьшает в нем число свободных переменных и превращает его в предикат от меньшего числа переменных.

Пример. Пусть – предикат « – четное число». Тогда высказывание истинно на любом множестве четных чисел и ложно, если содержит хотя бы одно нечетное число. Высказывание истинно на любом множестве, содержащем хотя бы одно четное число и ложно на любом множестве нечетных чисел.

Пример. Теорема Ферма формулируется, с помощью кванторов, следующим образом:

.

Пример. Пусть предикат описывает отношение « любит » на множестве людей. Для разных вариантов навешивания кванторов на обе переменные словесные интерпретации полученных формул будут различны:

– «для любого существует , которого он любит»,

– «существует такой , которого любят все »,

– «все люди любят всех людей»,

– «существует человек, который кого-то любит»,

– «существует человек, который любит всех»,

– «каждого человека кто-то любит».

2.5.3. Выполнимость и истинность

При логической интерпретации формул логики предикатов возможны три основные ситуации.

1. Если в области для формулы существует такая подстановка констант вместо всех переменных, что становится истинным высказыванием, то формула называется выполнимой в области М.

2. Если формула выполнима в при любых подстановках констант, то она называется тождественно истинной в . Формула, тождественно истинная в любых , называется тождественно истинной или общезначимой.

Пример. Формула тождественно истинна.

3. Если формула невыполнима в , то она называется тождественно ложной в . Если формула невыполнима ни в каких 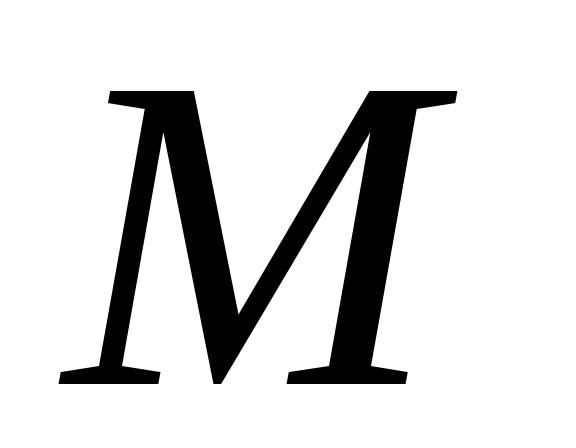, она называется тождественно ложной или противоречивой.

Пример. Формула тождественно ложна.

Определение. Моделью  в логике предикатов называют множество вместе с заданной на нем совокупностью предикатов : , где – основное множество модели ; – сигнатура модели .

Пример. Определить истинность, ложность или выполнимость на модели следующих формул:

Здесь – предикаты суммы, произведения и равенства.

Первая предикатная формула является тождественно истинной на модели  ввиду единственности значения произведения чисел из . При любых подстановках констант формула истинна.

Вторая формула на модели  выражает существование натурального квадрата натурального числа . Она также тождественно истинна на модели .

Третья формула выполнима на модели . Она читается –«существует натуральное значение квадратного корня для натурального числа из », или « – натуральное число». Очевидно, что она истинна при подстановках вместо чисел 0,1,4,9,16,… , и ложна при подстановке 2,3,5,…