2.4.4. Сокращенная днф

Определение. Интервал называется максимальным для , если и не существует интервала такого, что . При проверке отношения полезно иметь в виду, что оно выполняется тогда, и только тогда, когда , т.е. когда конъюнкция получается из конъюнкции вычеркиванием непустого числа сомножителей.

Очевидно, что каждый интервал содержится в некотором максимальном интервале . Поэтому совокупность всех максимальных для интервалов определяет покрытие подмножества .

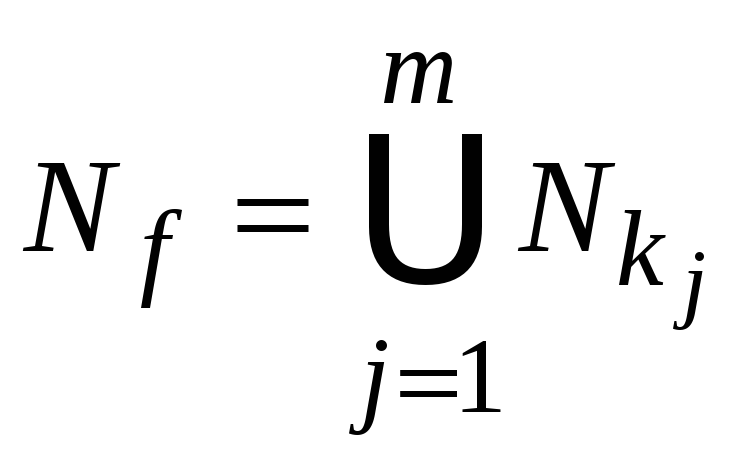О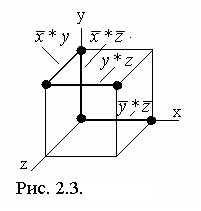пределение. ДНФ 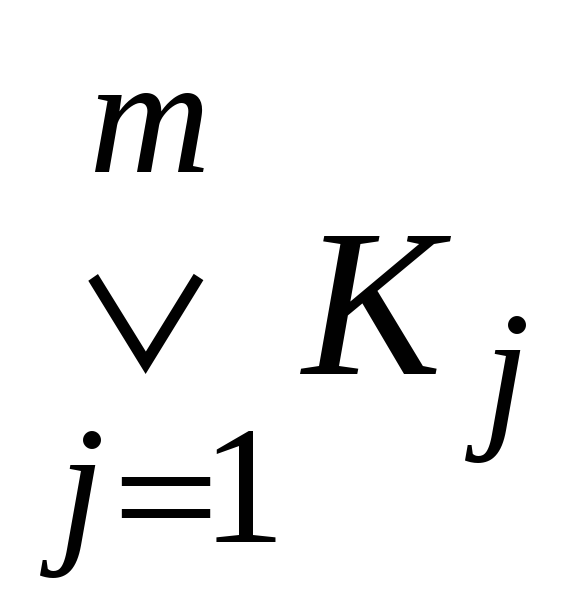, реализующая функцию и соответствующая покрытию подмножества всеми максимальными для интервалами, называется сокращенной ДНФ функции .

Пример. Из рисунка 2.3. следует, что область истинности включает четыре интервала 2–го ранга, которые образуют покрытие области истинности . Интервалов 1–го ранга здесь нет. Таким образом, полученная ДНФ является сокращенной ДНФ функции .

Сокращенная ДНФ не является, вообще говоря, минимальной ДНФ. В частности, минимальными для данной являются ДНФ и . Геометрически легко заметить, что эти формы соответствуют покрытию подмножества минимальным числом максимальных для интервалов. Алгебраически же, может быть сформулирована следующая теорема.

Теорема. Минимальная ДНФ функции получается из сокращенной ДНФ функции путем удаления некоторых элементарных конъюнкций.

Из данной теоремы следует, что при построении минимальных форм нет необходимости рассматривать все допустимые конъюнкции – достаточно ограничиться теми, которые входят в сокращенную ДНФ.

2.4.5. Построение сокращенной днф

Один из методов построения сокращенной ДНФ – геометрический, ранее уже был изложен. Он нагляден, однако его применимость ограничена функциями трех аргументов. Для функций с большим числом аргументов необходимы аналитические способы.

Существует целый ряд методов синтеза сокращенной ДНФ. Суть всех этих методов – в последовательном упрощении логического выражения, обычно заданного в виде СДНФ. В процессе упрощения используются следующие преобразования:

1) склеивание –

2) поглощение –

3) неполное склеивание –

4) обобщенное склеивание –

Рассмотрим один из методов получения сокращенной ДНФ из СДНФ, известный как метод Блейка–Порецкого [ ], который заключается в неполном попарном склеивании всех элементарных конъюнкций СДНФ между собой, и затем – использовании правила поглощения. Эта процедура повторяется для элементарных конъюнкций меньшего числа переменных до тех пор, пока склеивание станет невозможным. Не вдаваясь глубоко в теорию, рассмотрим пример.

Пример. Получить сокращенную ДНФ функции, заданной в виде совершенной дизъюнктивной нормальной формы .

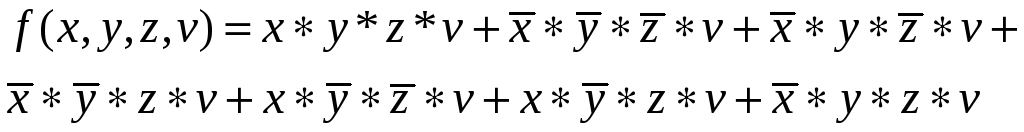С целью формализации процесса пронумеруем все конъюнкции СДНФ:

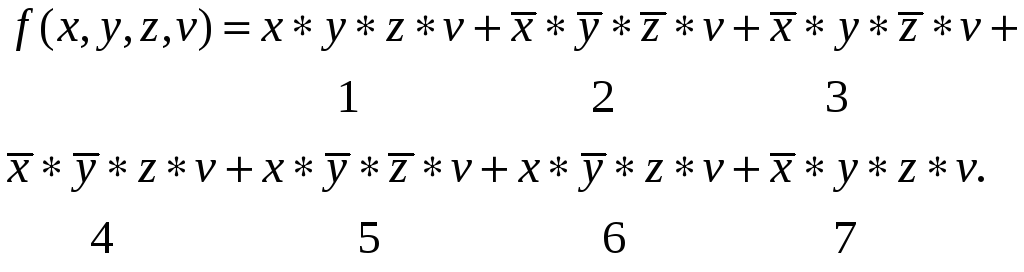
Выполним все возможные неполные попарные склеивания конъюнкций четырех переменных, нумеруя получающиеся конъюнкции трех переменных парой индексов, относящихся к исходным конъюнкциям. Получим:

Теперь проведем процедуру поглощение конъюнкций. Легко видеть, что все конъюнкции четырех переменных поглощены коньюнкциями трех переменных. В результате получим:

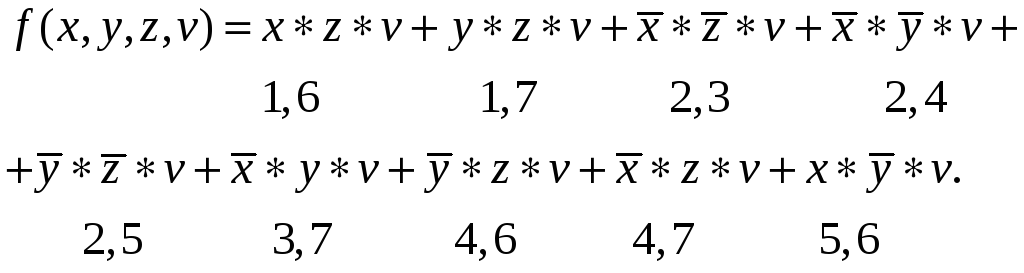
Аналогичным образом выполним все возможные неполные попарные склеивания полученных элементарных конъюнкций трех переменных и проведем процедуру поглощения. В итоге имеем:

.

Дальнейшее склеивание невозможно, следовательно, сокращенная дизъюнктивная нормальная форма получена.