1.2 Способы задания множеств

1. Перечислением, списком своих элементов.

Пример:

Множество натуральных чисел не превышающих 6, списком задается следующим образом: N={1, 2, 3, 4, 5, 6}

2.Порождающей процедурой.

Процедура описывает способ получения элементов множества из уже полученных элементов, либо других объектов.

Пример:

Множество целых чисел, являющихся степенями двойки и не превышающих 16, порождающей процедурой задается следующим образом:

Обозначим множество М₂n, n N, где N – множество натуральных чисел

1) 1 М₂n. 2) Если m N, то 2m М₂n. 3) m ≤ 8.

Списком это множество задается так: М_2n= {1, 2, 4, 8, 16}

3.Описанием характеристических свойств, которыми обладают элементы.

А= {x|P (x)} или А={x:P(x)}

(множество А состоит из элементов x таких, что x обладает свойством P).

Пример:

Описанием характеристических свойств множество натуральных чисел задается следующим образом:

N={x: x– целое положительное число}

Пример:

Конечное множество корней уравнения

x²- 3x+ 2 = 0 может быть задано так: A={x|x² - 3x + 2 = 0}.

Пример:

Задать различными способами множество всех четных чисел 2, 4, 6... не превышающих 20.

Решение:

1) списком М_2n = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}.

2) Порождающей процедурой:

а) 2М_2n;

б) если х М_2n, то (х+2)М_2n ;

в) х ≤ 18.

3) описаниям характеристических свойств:

М_2n = {х:|х –четное число, не превышающее 20}.

1.3 Операции над множествами

1. Объединением множеств А и В (АВ) называется множество, состоящее из всех тех элементов, принадлежащих хотя бы одному из этих множеств.

(АB={x | х  А x В}

Для пустого множества: А =A, 

2. Пересечением множеств А и В (АВ) называется множество, состоящее из всех элементов, принадлежащих как одному, так и другому множеству.

АВ={ x | xАx В}

Для пустого множества А, 

3. Разностью двух множеств (А и В) называется множество, состоящее из всех элементов, принадлежащих множеству А, но не принадлежащих множеству В.

А\ В= { x|x А x В}

4. Дополнение (до U) множества А (обозначение Ā) называется множество всех элементов, не принадлежащих А, но принадлежащих U. Множество U, такое, что все рассматриваемые множества являются его подмножествами, называется универсальным.

Ā=U\А.

Пример:

Пусть U ={1, 2, 3, 4, 5, 6}, А={1, 2, 4, 6}, В={3, 4, 5, 6}, С={1, 3, 5}

Найти:

Решение: .

.

.

.

.

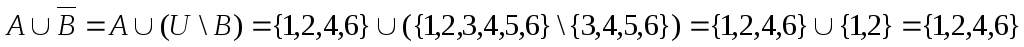
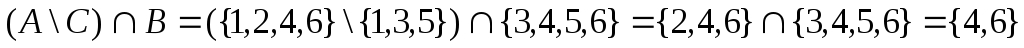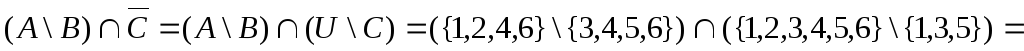
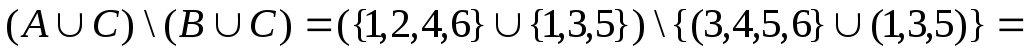
1.4 Графическое представление множеств

Отношения между множеством иллюстрируются при помощи специальных диаграмм – диаграмм Венна (Джон Венн - английский ученый (1834 - 1923)).

Построение диаграмм заключается в изображение прямоугольника, представляющего множество U, а внутри его кругов, представляющих множества.

Фигуры соответствующим образом обозначаются. Необходимые области заштриховываются.

Все операции, описанные выше можно представить на диаграммах Венна следующим образом: объединение множеств (рис. 1.1), пересечение множеств (рис. 1.2), разность множеств (рис. 1.3), дополнение до универсального множества (рис. 1.4).

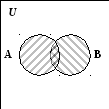
А

Рис. 1.1

Рис. 1.2

 B A  B

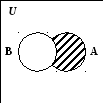
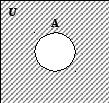
A

Рис. 1.3

Рис. 1.4

\B A

Пример:

Проиллюстрировать с помощью диаграмм Венна справедливость соотношения:

А(В С)=(АВ)  (АС).

Решение: а)Изобразим А(ВС):

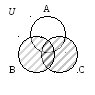
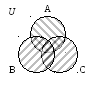
В  С А(ВС)

б) Изобразим (АВ)  (АС)

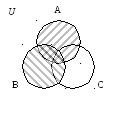
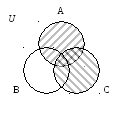
АВ AС

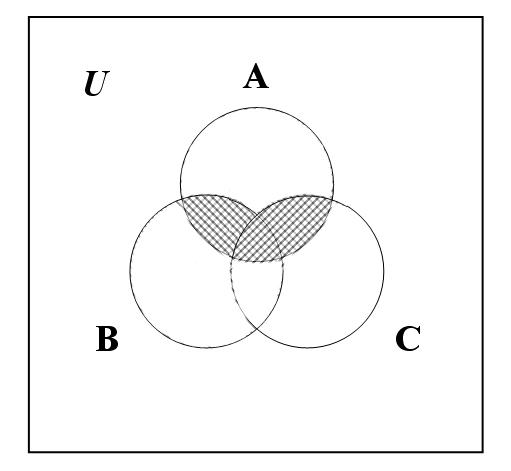
(А В)  (АС)