7.2. Постулаты специальной (частной) теории относительности. Преобразования Лоренца

Эйнштейн сформулировал два постулата, лежащие в основе специальной теории относительности:

1. Физические явления во всех инерциальных системах отсчета протекают одинаково. Никакими физическими опытами, проведенными внутри замкнутой инерциальной системы отсчета, нельзя обнаружить, покоится ли эта система или движется равномерно и прямолинейно.

2. Скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от скорости движения источника света или наблюдателя.

Наличие этих постулатов позволяет получить новые преобразования координат, отличающиеся от (7.1).

Пусть система движется относительно инерциальной системы K с постоянной скоростью v_о (рис. 7.1) так, чтобы оси x и при движении совпадали, а оси y, и z, были параллельны друг другу, причем вектор, соединяющий начала координат, , где t время. Можно показать, что координаты y и z связаны формулами y = ; z = . Ищем зависимость между подвижными и неподвижными координатами x в виде

, (7.2)

где  искомый коэффициент. Согласно первому постулату в силу равноправия систем отсчета для перехода от неподвижной системы отсчета к подвижной зависимость между координатами должна иметь аналогичный вид и отличаться лишь знаком для скорости v_o:

= (x - v_o, t). (7.3)

Пусть в моменты времени t = = 0 в точке x = = 0 в направлении оси x испускается вспышка света. Это событие через время t будет наблюдаться в точке x = ct и через время в точке = c . Здесь используется тот факт, что скорость света c для вакуума согласно 2^му постулату Эйнштейна одинакова в обеих системах. Подставляя в два последних равенства выражения (7.2) и (7.3), получим (c + v_o)= ct ; (c - v_o)t = c. Перемножая эти два равенства, получим  = 1/(1 -  ²)^0,5 , где величину  = v_o /c называют относительной скоростью.

Исключая из равенств (7.2) и (7.3) координату x, получим

t = / +  /c

Подставляя в эту формулу и в формулу (7.2) выражения для  и , получим окончательно формулы для связи координат и времени :

(7.4)

Полученные формулы называют преобразованиями Лоренца. Ученый Лоренц впервые получил эти формулы и показал, что если уравнения Максвелла преобразовать подстановкой (7.4), то их вид останется прежним и эти уравнения подчиняются принципу относительности. Эйнштейн предположил, что все физические законы не должны меняться от преобразований Лоренца.

Преобразования Лоренца при малых скоростях движения (  0) переходят в преобразования Галилея, которые являются предельным случаем преобразований Лоренца. Из преобразований Лоренца следует, что как пространственные, так и временные преобразования не являются независимыми. Таким образом, теория Эйнштейна оперирует не с трехмерным пространством, а рассматривает неразрывно связанные пространственные и временные координаты, образующие четырехмерное пространство-время.

Теорию относительности часто называют релятивистской теорией, а специфические явления, описываемые этой теорий, - релятивистскими эффектами.

7.3. Следствия из преобразований Лоренца.

Самым неожиданным следствием теории относительности является зависимость времени от системы отсчета.

Длительность событий в разных системах отсчета. Пусть в некоторой точке , покоящейся относительно подвижной системы , происходит событие, длительность которого = - , где и - начальный и конечный промежутки времени. C помощью формул (7.4) получим, что длительность этого же события в неподвижной системе отсчета K равна

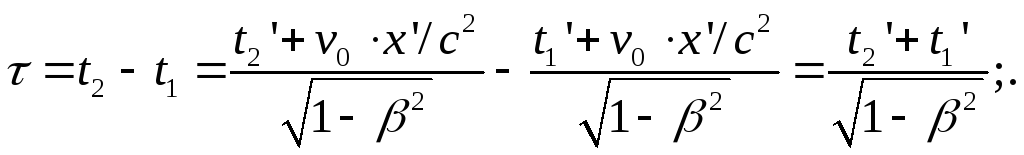
или

(7.5)

И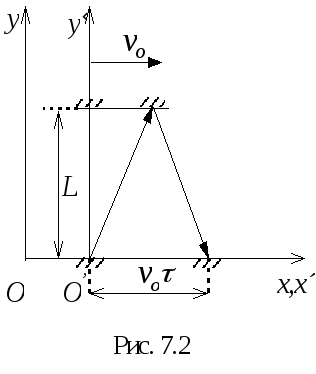з последнего равенства следует, что , т.е. для подвижной системы отсчета событие будет происходить за меньший промежуток времени. Следовательно, для подвижной системы отсчета время идет медленнее. Этот удивительный результат можно понять, если придумать специальные часы, в которых роль маятника играет световой сигнал, бегающий между двумя параллельными зеркалами, находящимися на расстоянии L. Период таких часов для системы отсчета, в которой они покоятся = 2L /с. Если эти часы движутся со скоростью v_o вдоль оси x (рис. 7.2), то для неподвижного наблюдателя траектория движения луча выглядит в виде зигзага и расстояние, пройденное светом за период часов  , будет более длинным, его квадрат равен 4L² + ² = с²² . Исключая L из двух последних равенств, легко получить выражение (7.5)  =/(1--  ²)^0,5. Если космонавт улетит от Земли со скоростью, близкой к скорости света (например,  ² = 1 - 10^-4 ), и вернется обратно через год, то по земным часам полет продлится 100 лет. Космонавт возвратится на Землю в сто раз более молодым, чем его брат-близнец. Данный результат мысленного эксперимента кажется неправильной интерпретацией преобразований Лоренца, так как, если за неподвижную систему отсчета считать движущийся корабль, то его близнец на Земле удаляется с такой же скоростью, и его время как бы замедлится по сравнению с часами на корабле. Однако эти две системы – не равнозначны, космонавт на корабле должен ускоряться и замедляться, чтобы вернуться на Землю. Поэтому система отсчета, связанная с кораблем ‑ неинерциальна. Получается, что причина замедления физических процессов связана с тем, что космонавт при путешествии подвергался дополнительным механическим перегрузкам. Детальный расчет, выходящий за рамки специальной теории относительности, показывает, что часы, движущиеся с ускорением, идут медленнее, поэтому при возвращении отстанут именно они.

Эффект замедления хода часов получил экспериментальное подтверждение при исследовании частиц -мезонов, образующихся в космических лучах. Среднее время жизни неподвижных -мезонов составляет 210^-6с. Казалось бы, что двигаясь со скоростью света -мезоны могут пройти расстояние 600м. Однако -мезоны проходят расстояние 20-30 км и достигают земной поверхности, т.е. для земного наблюдателя время жизни -мезонов оказывается гораздо большим.

Одновременность событий в разных системах отсчета. Пусть в подвижной системе в точках с координатами и происходят одновременно два события в момент времени = = b . Согласно формулам (7.4) в системе K этим событиям будут соответствовать координаты t₁ = (b + v_o /c²)/(1- -  ²)^0,5 и t₂ = (b +v_o /c²)/(1- ²)^0,5 . Из написанных формул видно, что если события в системе K пространственно разобщены (  ), они не будут происходить одновременно. Например, при  получим t₁  t₂ , т.е. событие в точке 1 для неподвижной системы отсчета произойдет раньше, хотя для подвижной системы эти события одновременны.

Длина тел в разных системах отсчета. Из преобразований (7.4) следует, что при движении тел их размеры по осям x и y не изменяются. Пусть в системе K покоится стержень, параллельный оси x . Длина его, измеренная в этой системе, равна l = x₂ - x₁ , где x₁ и x₂ - координаты обоих концов стержня в системе K . Используя преобразования Лоренца (7.4), выразим длину стержня в следующем виде l = ( + v_o)/(1-  ²)^0,5 - ( + + v_o)/(1-  ²)^0,5 = ( - )/(1- ²)^0,5 , где и - координаты концов стержня, измеренные в подвижной системе в один и тот же момент времени . Длина стержня в системе равна = - . Окончательно получим l = /(1-  ²)^0,5 или = l(1-  ²)^0,5 . Отсюда следует l  . Длину l называют собственной длиной стержня в той системе отсчета, в которой он покоится. Это наибольшая длина стержня. Если предмет начинает двигаться, его размеры в направлении оси x сокращаются пропорционально (1-  ²)^0,5 . Например, если неподвижное тело является шаром, то при движении шар сжимается вдоль оси x , приобретая форму эллипсоида вращения.

Релятивистский закон сложения скоростей. Пусть опять система движется относительно системы K со скоростью v_o вдоль оси x . Пусть v_x = dx/dt есть компонента скорости некоторой частицы в системе K , а = - компонента скорости ее в системе . Дифференцируя формулы (7.4), получим

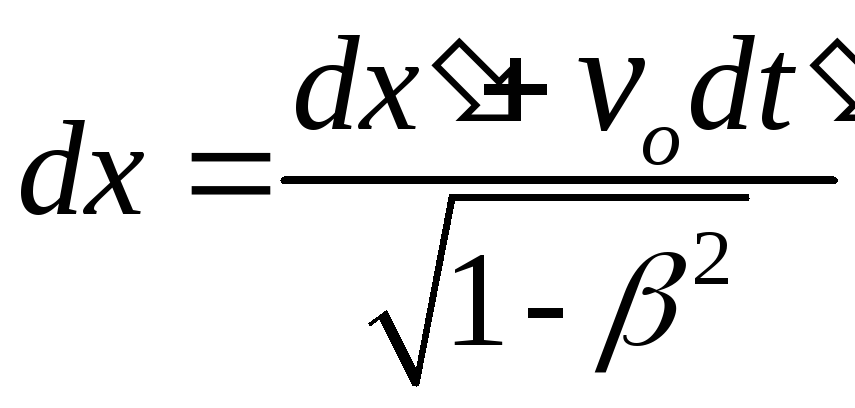; dy = d; dz = dz’; .

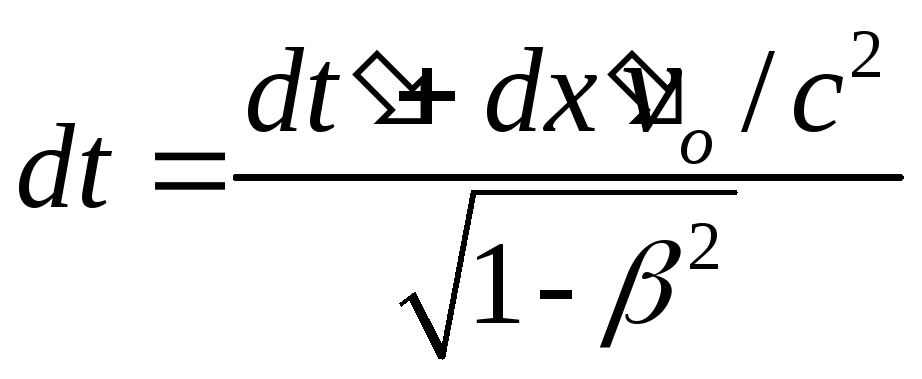Разделив первые три равенства на четвертое и учитывая, что  = v_o/c, находим

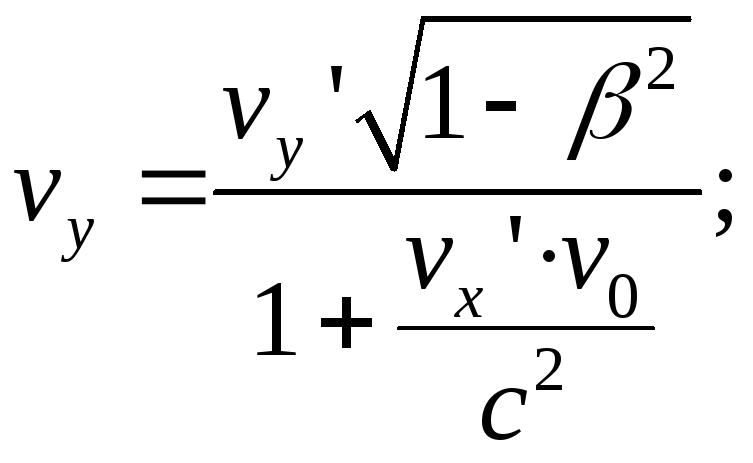
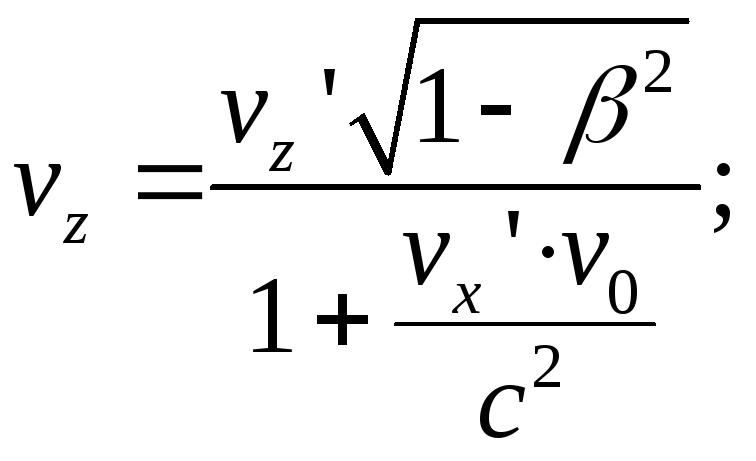(7.6)

где v_x , v_y , v_z - составляющие скорости частицы в системе K , , , - составляющие скорости частицы в системе . Полученные формулы и определяют преобразование скоростей. При с  релятивистские формулы переходят в формулы классической механики.

Пусть корабль движется вдоль оси x со скоростью = c / 2 и некоторая частица движется в этом же направлении относительно корабля со скоростью = c / 2 . По формулам (7.6) получим v_x = 4c/5 , т.е. по теории относительности 1/2 и 1/2 дают не 1, а 4/5.

Возьмем предельный случай. Положим, что человек на борту корабля наблюдает, распространение света вдоль оси x , т.е. = с. Тогда по формулам (8.6) получим v_x = (с + )/(1 + c/c²) = c . Итак, скорость света для неподвижного наблюдателя опять равна скорости света.