30. Методика изучения производной, интеграла и их применений.
При изучении темы "Производная" проявляются известные трудности, связанные с осуществлением предельных переходов. Важно поэтому придать изложению возможно более наглядный и конкретный характер.
Определению производной функции как предела разностного отношения предшествует рассмотрению особенностей поведения графиков гладких функций, приводящее к понятию касательной. Производная функции появляется сначала как тангенс угла наклона касательной к оси абсцисс. Тем самым с понятием производной на первом этапе связывается наглядный образ – касательная. Предельные переходы появляются как средство вычисления производной.
При изучении применения производной существенная роль отводится наглядным представлениям о производной. Опора на геометрический и механический смысл делают интуитивно ясными критерии возрастания и убывания функций, признаки максимума минимума.
Методическая схема изучения производной
-
Привести подводящую задачу, раскрывающую физический смысл понятия производной: свободное падение тела, которое не является равномерным.
-
Сформулировать определение понятия производной.
Так как в определении отсутствует понятие предела, то первоначально следует сформировать у учащихся понятие приращения как изменения и аргумента и функции.
После рассмотрения геометрического смысла производной вводим определение:
Производной функции в точке х0 называется число, к которому стремится разностное отношение:
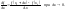
Полезен
небольшой анализ формулировки
определения, позволяющий чётче выделить
признаки данного понятия: 1) число, 2) к
которому стремится разностное отношение
-
Конкретизировать понятие производной (путём вычисления производной по определению: выяснение её геометрического смысла, графическое отыскание производной)
Методика введения понятия интеграл
• Определение криволинейной трапеции.
Фигуру, ограниченную на отрезке [ a ; b ] непрерывной и не меняющей на нём знака функцией f ( x ), осью Ох и прямыми x = a , x = b называют криволинейной трапецией. { Обратить внимание учащихся на примеры криволинейных трапеций}
• Задача о площади криволинейной трапеции.
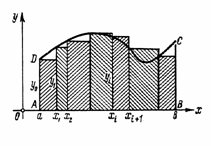
Для вычисления площади этой трапеции разобъём отрезок [ a ; b ] на n отрезков и на каждом из них построим прямоугольник. Площадь каждого из них равна произведению высоты на основание f ( x i )? x , где ? x = x i +1 – x i . Площадь всей трапеции равна сумме площадей всех прямоугольников
Sn = f ( x 1 )? x 1 + f ( x 2 )? x 2 + … f ( x n )? x n .
• Понятие интеграла.
Но эта формула даёт лишь приближённое значение площади. Точное значение площади мы получим как предел этой суммы.
,
где ? x 
0.
Этот предел и называют определённым
интегралом и обозначают
f ( x ) – подинтегральная функция, а и b – нижний и верхний пределы интегрирования.
• Формула Ньютона – Лейбница
Теорема . Пусть функция f ( x ) определена и непрерывна на отрезке [ a ; b ], а определённая и непрерывная на отрезке [ a ; b ] функция F ( x ) – одна из её первообразных. Тогда имеет место формула
Доказательство:
Так как функция F ( x ) первообразная для
функции f ( x ), то имеет место равенство:
где С – некоторая постоянная. Положим в этом равенстве х = а. Учитывая, что
получим С = - F ( a ). Подставляя это выражение получаем
Полагая в ней х = b получим требуемое утверждение.
Эта формула носит название формулы Ньютона –Лейбница. Она позволяет во многих случаях просто вычислять определённый интеграл. Но пользоваться ей лучше в таком виде:
