Розклад даного вектора за напрямками на прямій, на площині і в просторі

Означення: Вектор називається лінійною комбінацією п векторів , де - деякі числові множники.

Вираз називається розкладом вектора за системою векторів .

Перейдемо до лінійного вираження вектора за напрямком у більш загальній формі: на прямій, на площині, у просторі.

1. На прямій дано два ненульові і колінеарні вектори і , тобто . Існує таке число , що .

2. На площині дано два не колінеарні вектори і та вектор , що належить тій же площині . Знайти розклад вектора за напрямком векторів і .

В

За відомим із шкільного курсу правилом паралелограма , , і . Тоді є лінійною комбінацією двох векторів і .

3. В просторі задано три не компланарні вектори і вектор . Знайти розклад вектора за напрямком векторів .

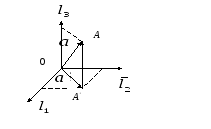
Із пункту 2 видно, що розклад вектора на площині векторів і має вигляд . Із правила паралелограма , а . Тоді є лінійною комбінацією трьох векторів .

Лінійна залежність і лінійна незалежність системи векторів

Означення: Система векторів називається лінійно залежною, якщо їх лінійна комбінація дорівнює нульовому вектору за умови, що хоча б один із коефіцієнтів відмінний від нуля.

Якщо система векторів є лінійно залежною, то хоча б один із векторів можна подати у вигляді лінійної комбінації інших. Нехай , тоді

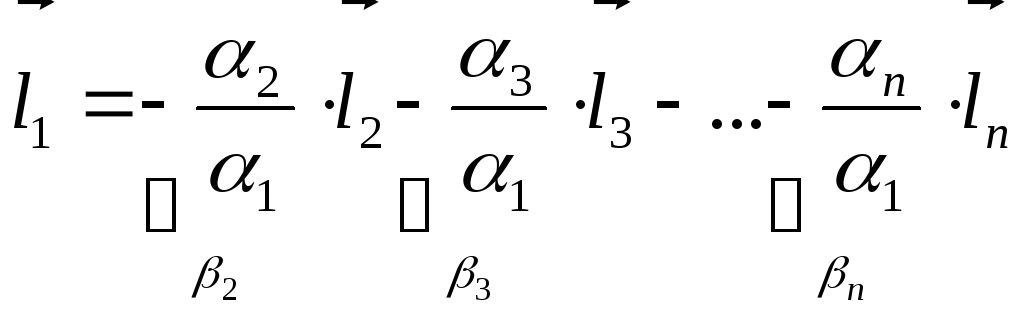, або

.

Означення: Система векторів називається лінійно незалежною, якщо їх лінійна комбінація дорівнює нульовому вектору за умови рівності нулю всіх коефіцієнтів ,

.

Поняття лінійної залежності векторів дозволяє характеризувати їх взаємне положення у просторі. Так, два вектори залежні тоді і тільки тоді, коли вони колінеарні. Три вектори лінійно залежні тоді і тільки тоді, коли вони компланарні. Чотири вектори завжди лінійно залежні, тобто існують числа такі, що для векторів має місце розклад вектора .

Базис

Означення: Система лінійно незалежних векторів простору, за якими можна розкласти довільний вектор, називається базисом цього простору.

Вектори , що утворюють базис, називаються базисними.

Використовуючи вищевикладене можна зробити висновки, що на прямій базисним може бути всякий ненульовий вектор, а на площині утворюють базис будь-які два не колінеарні вектори, а всякий компланарний з ними може бути розкладений у цьому базисі.

Декартова прямокутна система координат

Декартова прямокутна система координат складається з трьох взаємно перпендикулярних осей (Ох – абсцис, Оу – ординат, Оz – аплікат) і точки О – їх перетину та заданого масштабу для вимірювання довжин будь-яких відрізків на площині або у просторі.

Одиничні вектори , що напрямлені за координатними осями , називаються ортами, а утворена ними система (базис) ортонормованим.

Розміщення точки в декартовій системі координат:

1) , тоді точка М належить площині yOz;

2) , тоді точка М належить площині хOz;

3) , тоді точка М належить площині хOу;

4) , тоді точка М належить осі Oz;

5) , тоді точка М належить осі Oх;

6) , тоді точка М належить осі Oу.

Координатами вектора називаються його проекції на координатні осі Ох, Оу, Оz і записують .

Координати вектора є його коефіцієнтами при розкладі вектора за ортами .

Координати визначають вектор. У рівних векторів рівні відповідні координати, тобто якщо дано вектори і , причому , тоді .

Вектор , що напрямлений із початку координат до точки називається радіус-вектором точки і має розклад .

Якщо вектор задано за допомогою координат точок його початку і кінця і одержуються за допомогою віднімання від координат кінця відповідних координат початку

.