Тема 3 Матриці

Означення: матрицею розміру називається прямокутна таблиця чисел, яка складається з рядків та стовпців. Числа з яких складається матриця, називається елементами матриці ().

Матриці позначаються великими (заглавними) літерами латинського алфавіту.

Наряду з круглими дужками використовують і інші [ ],.

Означення: дві матриці А і В однакових розмірів називаються рівними тоді і тільки тоді, коли рівні їх відповідні елементи .

Розглянемо основні типи матриць:

1. Нульовою називається матриця, всі елементи якої дорівнюють нулю.

2. Квадратною матрицею називається матриця, в якої кількість рядків дорівнює кількості стовпців

3. Діагональною матрицею називається така квадратна матриця, в якої елементи головної діагоналі відмінні від нуля, а всі решта елементів дорівнюють нулю.

4. Одиничною матрицею називається діагональна матриця, в якої всі елементи дорівнюють одиниці.

4. Матрицею-стовпцем називається матриця, що складається з одного стовпця

–матриця рядок

4. симетричною матрицею називається квадратна матриця, якщо , тобто рівні її елементи , симетричні відносно головної діагоналі

Лінійні дії над матрицями

1. Добутком числа на матрицю розміру називається матриця того ж розміру, кожний елемент якої дорівнює відповідному елементу матриці А помноженому на число

2. Сумою двох матриць 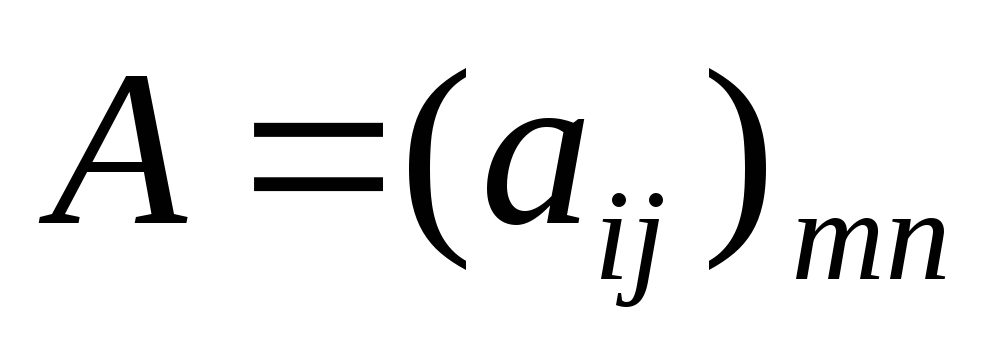і розміру називається матриця того ж розміру, кожний елемент якої дорівнює сумі відповідних елементів матриці доданків, тобто і позначається С=А+В.

Аналогічно дається означення різниці матриць:

Дії додавання, віднімання і множення на число називається лінійними діями над матрицями.

Властивості лінійних дій над матрицями

1. А+В=В+А –комутативний

2. (А+В)+С=А+(В+С) –асоціативний

3. А+0=А

4. А+(-А)=0

5. 

6. 

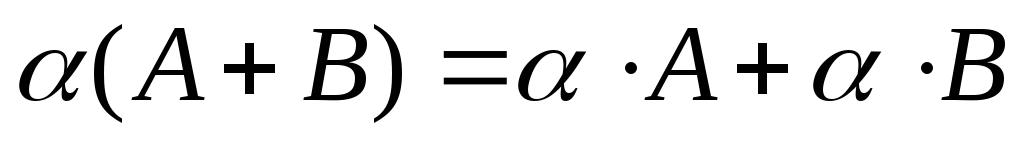7. – дистрибутивний

8. 

0 – нульова матриця -А –матриця, протилежна до матриці А

Множення матриць

Для множення матриці А розміру на матрицю В розміру – необхідна їх узгодженість.

Означення: матриці А і В називаються узгодженими, якщо число стовпців матриці А (першого співмножника) збігалося з числом рядків матриці В (другого співмножника).

У нашому випадку матриця А є узгодженою з матрицею В, але матриця В не є узгодженою з матрицею А.

Будь які квадратні матриці одного розмірі є узгодженими.

Означення: добутком матриці А розміру на матрицю В розміру називається матриця С розміру , елементи якої дорівнюють сумі добутків елементів і-того рядка матриці А на відповідні елементи j-того стовпця матриці В, тобто

Наприклад: знайти та

– комунікативний закон множення не виконується!

Властивості множення матриць

1. – асоціативність відносно множення

2. 

3. – дистрибутивний закон множення відносно додавання

4. 

Маємо на увазі, що матриці А,В,С – узгоджені.