3. Асимптоти кривих

Іноді про поводження графіка функції на окремих ділянках вдається судити, побудувавши прямі, називані асимптотами (тобто, що притягають до себе графік функції). Допустимо, що х₀ R-точка розриву другого роду функції f(х) і при прагненні х до х_о ліворуч (праворуч) функція монотонно росте (убуває), тобто монотонно прагне до + (— ), тоді відповідна галузь графіка «притискається» до вертикальній прямій х=х_о, ідучи нагору або вниз. У цьому випадку говорять, що пряма х=х_о є вертикальної асимптотою графіка.

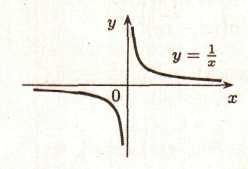
ПРИКЛАД 5. Ясно, що х = 0 є асимптотою графіка функції в = (див. мал. 4).

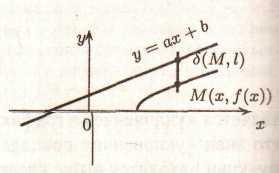
Визначення 6. Пряма l:в= ах+b називається асимптотою графіка функції в = f(x) при х→ + (- ), якщо

(5)

де δ(M(x,f(x)),l) -вертикальне відхилення точки M(x,f(x)), що належить графікові функції в = f(х), від прямій l. (Див. мал. 5)

ТЕОРЕМА 4

Для того щоб пряма в = ах+b була асимптотою графіка функції в=f(х) при х→ + (- ), необхідно й досить, щоб існували наступні межі:

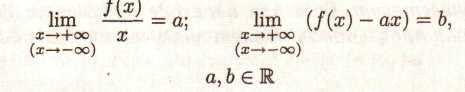
ПРИКЛАД 6. Знайти асимптоти графіка функції

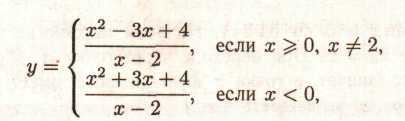
(якщо вони існують).

1. Ясно, що х = 2 є вертикальної асимптотою.

2. Знайдемо:

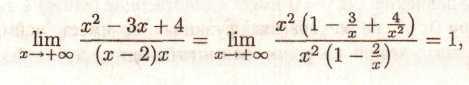
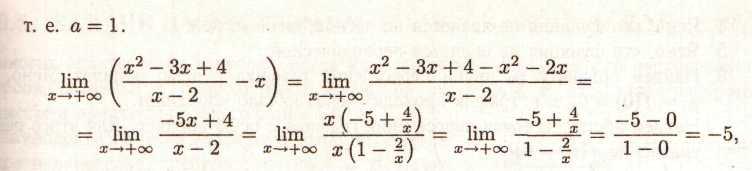
b = -5, т.e.при х→ + пряма в = х+5 є асимптотою.

3. Знайдемо

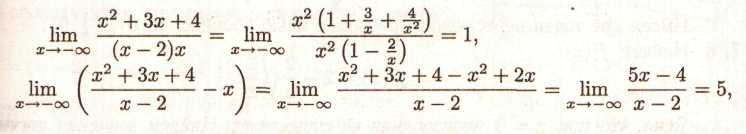
т. е. при х→- пряма в = х + 5 є асимптотою

Зауваження. Існують функції, графіки яких не мають асимптот, наприклад функція в=х²

4. Дослідження функцій і побудова їхніх графіків

Приведемо схему дослідження функції й побудови її графіка:

1. Знайти область визначення функції;

2. Знайти точки розриву функції й досліджувати їхній характер;

3. Знайти асимптоти (якщо вони є);

4. Досліджувати функцію на парність, непарність;

5. Досліджувати функцію на періодичність;

6. Знайти точки перетинання графіка функції з координатними осями;

1. Знайти похідну функції й з її допомогою визначити ділянки зростання, убування функції;

2. Знайти точки екстремуму, визначити їхній характер (min, max), знайти максимальне й мінімальне значення функції;

7. Досліджувати функцію на опуклість нагору, униз; знайти точки перегину.

ПРИКЛАД 19.7. Досліджувати функцію й побудувати її графік.

1. Область визначення функції— (— , + );

2. Функція безперервна на всій області визначення, точок розриву не має;

Тому що функція не має точок розриву, те її графік не має вертикальних асимптот. Знайдемо асимптоти при х→ + , х→ - .

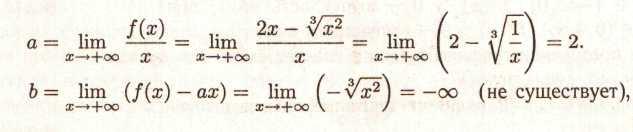
виходить, при х→ + графік функції не має асимптоти. Аналогічно показується, що при х→ - , асимптоти немає;

4. Ясно, що функція не є ні парної, ні непарної;

5. Ясно, що функція не є періодичною;

6. Знайдемо ординату у_о точки перетинання графіка з віссю ординат. Ясно, що в₀ =f(0) = 0, тобто графік проходить через початок координат.

Знайдемо абсциси точок перетинання графіка з віссю абсцис. Для цього вирішимо рівняння f(x) = 0:

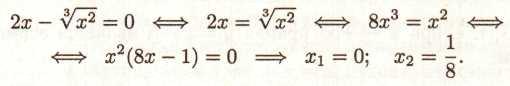
Маємо дві точки перетинання графіка з віссю абсцис: (0,0); ( ,0);

7, 8. Знайдемо

Ясно, що при х = 0 похідна не існує. Знайдемо значення аргументу, при яких похідна звертається в 0.

Визначимо знаки похідної на інтервалах

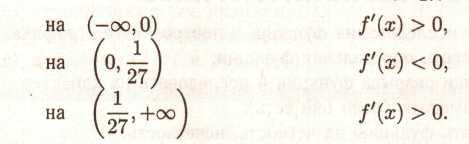
Складемо таблицю

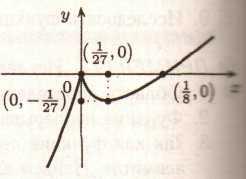9. Визначимо ділянки опуклості нагору, униз і точки перегину

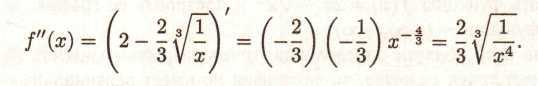
f" не існує в точці х = 0, а при всіх - опуклість униз, при - опуклість униз.

При побудові графіка функції варто мати на увазі, що

т. е. графік має в точці х = 0 вертикальну дотичну. Графік (його ескіз) наведений на мал. 6.