6.1. Інваріантість форми диференціала

Помітимо, що для функції f(x) = х, df = dx = 1* = , тому в правій частині формули для диференціала замість пишуть dx.

Нехай f : X→Y,g: Y→Z, X,Y,Z з R і f диференційована в точці x₀ € X, g диференційована в точці f(х_о), тоді по теоремі про похідну складну функцію (теорема 8) функція g°f диференційована в точці х_о. Маємо

(18)

Зрівняємо отриману формулу для диференціала складної функції g°f з формулою для диференціала функції g:

(19)

Зовні формули (18) і (19) практично не відрізняються. Цю властивість називають інваріантістю форми диференціала.

2. Геометричний зміст диференціала

Розглянемо графік функції в = f(x). Нехай вона диференційована в точці х_о. Як ми вже знаємо (§ 1), у цьому випадку можна говорити про дотичну до графіка функції в точці Mo(xo,f(xo)) і рівняння дотичної має вигляд

З малюнка 3 видно, що df -цей приріст ординати крапки на дотичній, коли аргумент одержав приріст .

Заміна функції в околиці крапки хо на дотичну до неї називається лінеаризацією.

Ясно, що

(20),

(21)

Більше точні методи наближення функції будуть розглянуті, коли ми будемо вивчати формулу Тейлора.

6.3. Диференціал суми, добутку, частки

З формули, що встановлює зв'язок між диференціалом і похідною

(22)

і теорем про похідну суму, добутку й частки треба

ТЕОРЕМА 10. Якщо f і g диференційовані в точці х_о, то f + g і g• f диференційовані в точці хо й мають місце формули

(23),(24)

TEOPEMA 11. Якщо f і g диференційовані в точці х_о й g(х_о)≠ 0, те диференційована в точці х_о й має місце формула

(25)

Наслідок з теореми 10. Якщо З — постійна й f -функція, диференційована в точці х₀, то функція Cf диференційована в точці х_о й має місце формула

(26)

Ясно, що d = 0 у будь-якій точці, тоді з формули (24) треба

Зауваження. Увівши позначення для диференціала й маючи формулу (22), ми одержимо вираження похідної через диференціали

(27)

7. Похідні й диференціали вищих порядків

Наприкінці § 2 ми говорили про похідній як про функції. Те ж саме можна сказати й про диференціал. Але тоді можна говорити й про похідній, тобто (f’(x))’ і т.д. Похідна похідній функції f називається похідній 2-го порядку й позначається f"(x), похідна від другої похідної функції f називається похідній 3-го порядку функції f і позначається f'"(x). Якщо у функції визначені похідні до до — 1 порядку включно, то можна ставити задачу відшукання похідній порядку до як похідній від похідної порядку до-1, тобто

(28)

Зауваження. Похідну функції f-f’(x) називають іноді похідній першого порядку, а саму функцію — похідній 0-го порядку.

Випишемо тепер визначення диференціалів 2-го, 3-го й т.д. порядків:

(29).

ПРИКЛАД 3.

1). Знайти

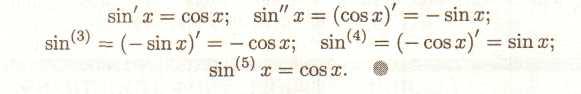
2). Знайти (х⁴)⁽⁷⁾

3). Знайти

Ясно, що

ТЕОРЕМА 12. Якщо функції f і g мають похідні до порядку п включно, то функція f+g має похідні до порядку п включно й має місце формула

, (30)

Ясно, що формула (30) — наслідок формули (23) і визначення похідній к-гo порядку

ТЕОРЕМА 13. Якщо f і g мають похідні до порядку т включно, то f°g має похідні до порядку m включно й має місце формула

(31)

Для п =1 формула (31) перетворюється у формулу (24) для похідної добутку, і виходить, справедлива.

Розглянемо випадок п = 2.

Припустимо, що формула (31) вірна для n₀, доведемо, що тоді вона вірна й для n₀+1

Індуктивний перехід доведений.

Відзначимо повну аналогію формули (31), що називають формулою Лейбніца, з формулою розкладання бінома Ньютона.

ПРИКЛАД 4. Знайти (sinх;cosx)⁽⁴⁾.

Тоді по формулі (31) для n=4 маємо

Зауваження. При рішенні приклада можна було обійтися без формули (31). Дійсно,