
- •Глава I. Действительные числа.
- •§1. Введение.
- •§2. Множества.
- •§3. Понятие множества действительных чисел.
- •§4. Отображения множеств.
- •Глава 2. Числовые последовательности.
- •§1. Понятие числовой последовательности.
- •§2. Бесконечно малые последовательности.
- •§3. Свойства сходящихся последовательностей.
- •Глава 3. Некоторые сведения из математической логики.
- •§1. Предложение.
- •§2. Предикаты.
- •§3. Кванторы.
- •§4. Предельный переход в неравенствах. (Глава 2)
- •§5. Бесконечно большие последовательности.
- •§6. Частичные последовательности (подпоследовательности).
- •§7. Монотонные последовательности.
- •§8. Теорема о вложенных отрезках.
- •§9. Теорема Больцано-Вейерштрасса.
- •§10. Критерий Коши сходимости числовой последовательности.
- •§11. Число .
- •Глава 3. Функции.
- •§1. Понятие числовой функции числового аргумента.
- •§2. Предел функции в точке.
- •§3. Арифметические свойства пределов функций.
- •§4. Предельный переход в неравенствах.
- •§5. Односторонние пределы функции в точке. (пределы слева и справа)
- •§6. Пределы функций на бесконечности.
- •§7. Функции, стремящиеся к бесконечности. (Бесконечно большие функции.)
- •§8. Сравнение бесконечно малых и бесконечно больших функций.
- •§9. Специальные пределы функций.
- •Глава 4. Непрерывность функции.
- •§1. Определение непрерывной функции.
- •§2. Классификация точек разрыва функции.
- •§3. Простейшие свойства непрерывных функций.
- •§4. Некоторые свойства непрерывных функций на промежутке.
- •§5. Условия непрерывности монотонной функции. Обратная функция. Непрерывность обратной функции.
- •Глава 5. Производная функции.
- •§1. Понятие производной функции.
- •§2. Свойства производной функции.
- •§3. Производная обратной функции.
- •§4. Таблица производных.
- •Глава 6. Дифференцируемая функция. Дифференциал.
- •§1. Понятие дифференцируемой функции в точке и дифференциала.
- •§2. Некоторые свойства дифференциала функции в точке.
§7. Монотонные последовательности.
Теорема.
Любая монотонная ограниченная последовательность сходится.
Доказательство.
-
Пусть {xn} возрастает и ограничена сверху, то есть x1
 x2
x2 …
…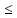 xn
xn …
и
…
и
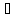 В
В
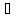 n:
xn
n:
xn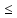 В.
В.
Так
как множество {xn}
всех элементов последовательности
ограниченно сверху, то
 sup
{xn}=а.
sup
{xn}=а.
Докажем,
что
 xn=а.
xn=а.
sup
{xn}=a
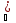 1)
1)
 n:
xn
n:
xn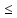 а
а
2)
 0
0
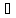 N:
xn>а-
N:
xn>а-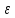 ,
а в силу возрастания {xn}
,
а в силу возрастания {xn}
 n>N:
а-
n>N:
а-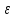 <xN
<xN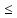 xn
xn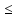 а<а+
а<а+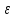
 а-
а-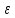 <xn<а+
<xn<а+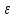
 │xn-а│<
│xn-а│<

 xn=а.
xn=а.
2) 1)
2. Пусть {xn} убывает и ограничена снизу.
Тогда
{-xn}
возрастает и ограничена сверху. В самом
деле x1 x2
x2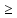 …
… xn
xn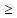 …
…
 - x1
- x1 -
x2
-
x2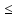 …
…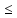 -
xn
-
xn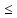 …
…
{xn}
ограничена снизу

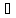 А
А
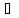 n:
А
n:
А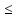 xn
xn
 - xn
- xn -А
-А
 {-xn}
ограничена сверху и возрастает. Тогда
по доказанному в п.1
{-xn}
ограничена сверху и возрастает. Тогда
по доказанному в п.1
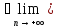 (-xn)=-а=sup
{-xn}.
А тогда а=
(-xn)=-а=sup
{-xn}.
А тогда а=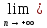 xn=
inf
{xn}.
xn=
inf
{xn}.
Следствие.
Любая
возрастающая (убывающая) последовательность
либо сходится к своей точной верхней
грани (соответственно, к своей точной
нижней грани), либо стремится к +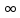 (соответственно, к -
(соответственно, к -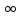 )
)
§8. Теорема о вложенных отрезках.
Теорема.
Пусть последовательность отрезков (1) { [an, bn] } удовлетворяет следующим условиям:
1).
 n:
[an+1,
bn+1]
n:
[an+1,
bn+1]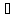 [an,
bn]
[an,
bn]
2).
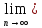 дл.[an,
bn]=
дл.[an,
bn]=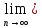 (bn-
an)=0
(bn-
an)=0
Тогда
последовательность концов отрезков
{an}
и {bn}
сходится и
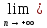 an=
an=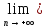 bn=с.
bn=с.
При этом с является единственной точкой, принадлежащей всем отрезкам последовательности (1).
Доказательство.
Рассмотрим последовательность {an} левых концов отрезков .
Из
условия 1) следует, что
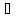 n,
n=1, 2, …: аn+1
n,
n=1, 2, …: аn+1 an
an
 {an}
возрастает. А так как
{an}
возрастает. А так как
 n:
an
n:
an b1
(an
b1
(an bn
bn b1),
то {an}
ограничена сверху.
b1),
то {an}
ограничена сверху.
 {an}
возрастает и ограничена сверху, а тогда
по теореме §7 она сходится
{an}
возрастает и ограничена сверху, а тогда
по теореме §7 она сходится

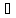 с:
с=
с:
с=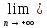 an.
an.
Рассмотрим теперь последовательность {bn} правых концов отрезков [an, bn], n=1, 2, …
Так
как для любого
n: bn=an+(bn-an),
то по теореме о пределе суммы двух
сходящихся последовательностей {an}
и {bn-an}
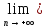 bn=с+0=с.
bn=с+0=с.
Согласно
следствию §7
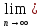 an=с=sup
{an},
а так как {bn}
убывает и ограничена снизу, то
an=с=sup
{an},
а так как {bn}
убывает и ограничена снизу, то
 bn=с=inf
{bn}.
bn=с=inf
{bn}.
По определению sup {an} и inf {bn}:
 n:
an
n:
an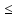 с
с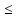 bn
bn

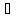 n:
с
n:
с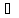 [an,
bn].
[an,
bn].
Докажем теперь, что точка с - единственная точка, принадлежащая всем отрезкам последовательности (1).
Предположим,
что
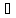 с′,
с′
с′,
с′ с
и такое, что
с
и такое, что
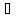 n:
с′
n:
с′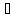 [an,
bn].
[an,
bn].
Значит,
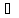 n:
n:


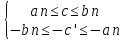
 -( bn-
an)
-( bn-
an)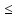 с-
с′
с-
с′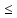 bn-
an,
а так как с′
bn-
an,
а так как с′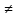 с,
то |с- с′|>0
с,
то |с- с′|>0
 0<|с- с′|
0<|с- с′|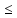 (bn-
an).
(bn-
an).
Но
это противоречит тому, что
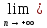 (bn-
an)=0.
(bn-
an)=0.
Замечание 1.
О последовательности (1) { [an, bn] } говорят, что { [an, bn] } – последовательность стягивающихся отрезков.
Замечание 2.
Если в условии теоремы отрезки заменить на промежутки другого типа, то сходимость последовательностей концов промежутков будет иметь место.
Второе утверждение теоремы может оказаться ложным.
Пример.
{(0,
1); (0,
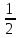 );
…; (0,
);
…; (0,
 );
…} имеет пустое пересечение.
);
…} имеет пустое пересечение.
§9. Теорема Больцано-Вейерштрасса.
Теорема.
Любая ограниченная числовая последовательность содержит сходящуюся подпоследовательность.
Доказательство.
Пусть
{xn}
– ограниченная последовательность

 а1
а1
 b1
b1
 n:
a1
n:
a1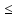 xn
xn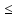 b1
b1

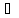 n:
xn
n:
xn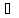 [a1,
b1].
[a1,
b1].
Разделим
отрезок [a1,
b1]
пополам и выберем ту половину, которая
содержит бесконечно много элементов
последовательности {xn}.
Получим отрезок [a2,
b2]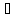 [a1,
b1].
[a1,
b1].
Делим отрезок [a2, b2] пополам и выбираем ту половину, которая содержит бесконечно много элементов последовательности {xn}. Получаем отрезок [a3, b3] и т.д.
Продолжая
этот процесс неограниченно, мы получим
последовательность вложенных отрезков
{ [an,
bn]
}
 такую, что
такую, что
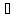 k:
[ak+1,
bk+1]
k:
[ak+1,
bk+1] [ak,
bk]
и
[ak,
bk]
и
 дл.[ak,
bk]=
дл.[ak,
bk]= =0.
=0.
Начнём теперь выбирать подпоследовательность последовательности {xn}.
В отрезке [a1, b1] возьмём xn1.
В отрезке [a2, b2] возьмём xn2 такое, что n2>n1
…
В отрезке [ak, bk] возьмём xnk, nk>nk-1
…
Продолжая
процесс выбора неограниченно, мы получим
последовательность {xnk}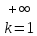 - подпоследовательность последовательности
{xn}
такую, что
- подпоследовательность последовательности
{xn}
такую, что
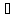 k:
ak
k:
ak xnk
xnk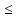 bk
bk
По
теореме о вложенных отрезках
последовательности концов {ak}
и {bk}
сходятся и
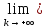 ak=
ak=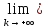 bk=с.
bk=с.
Но
тогда по теореме 2 §4 (предельный переход
в неравенствах для трёх последовательностей)
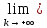 xnk=с.
xnk=с.
