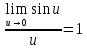- •Глава I. Действительные числа.
- •§1. Введение.
- •§2. Множества.
- •§3. Понятие множества действительных чисел.
- •§4. Отображения множеств.
- •Глава 2. Числовые последовательности.
- •§1. Понятие числовой последовательности.
- •§2. Бесконечно малые последовательности.
- •§3. Свойства сходящихся последовательностей.
- •Глава 3. Некоторые сведения из математической логики.
- •§1. Предложение.
- •§2. Предикаты.
- •§3. Кванторы.
- •§4. Предельный переход в неравенствах. (Глава 2)
- •§5. Бесконечно большие последовательности.
- •§6. Частичные последовательности (подпоследовательности).
- •§7. Монотонные последовательности.
- •§8. Теорема о вложенных отрезках.
- •§9. Теорема Больцано-Вейерштрасса.
- •§10. Критерий Коши сходимости числовой последовательности.
- •§11. Число .
- •Глава 3. Функции.
- •§1. Понятие числовой функции числового аргумента.
- •§2. Предел функции в точке.
- •§3. Арифметические свойства пределов функций.
- •§4. Предельный переход в неравенствах.
- •§5. Односторонние пределы функции в точке. (пределы слева и справа)
- •§6. Пределы функций на бесконечности.
- •§7. Функции, стремящиеся к бесконечности. (Бесконечно большие функции.)
- •§8. Сравнение бесконечно малых и бесконечно больших функций.
- •§9. Специальные пределы функций.
- •Глава 4. Непрерывность функции.
- •§1. Определение непрерывной функции.
- •§2. Классификация точек разрыва функции.
- •§3. Простейшие свойства непрерывных функций.
- •§4. Некоторые свойства непрерывных функций на промежутке.
- •§5. Условия непрерывности монотонной функции. Обратная функция. Непрерывность обратной функции.
- •Глава 5. Производная функции.
- •§1. Понятие производной функции.
- •§2. Свойства производной функции.
- •§3. Производная обратной функции.
- •§4. Таблица производных.
- •Глава 6. Дифференцируемая функция. Дифференциал.
- •§1. Понятие дифференцируемой функции в точке и дифференциала.
- •§2. Некоторые свойства дифференциала функции в точке.
§9. Специальные пределы функций.
Функция
f(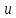 )=
)=
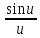 определена на Х=(
определена на Х=( ,
0)
,
0) (0,
+
(0,
+ ),
точка
),
точка
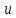 о=0
является концом одновременно двух
смежных промежутков из Х. так как
рассматриваем
о=0
является концом одновременно двух
смежных промежутков из Х. так как
рассматриваем
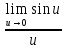 ,
то достаточно рассмотреть этот предел
для сужения
нашей функции f(
,
то достаточно рассмотреть этот предел
для сужения
нашей функции f( ),
то есть для функции
),
то есть для функции
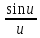 ,
,
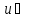 (
(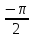 ,
0)
,
0)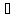 (0,
(0,
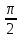 ).
).
Рассмотрим каждый интервал отдельно.
-
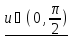

 >0,
tg
>0,
tg
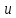 >0.
>0.
u
y
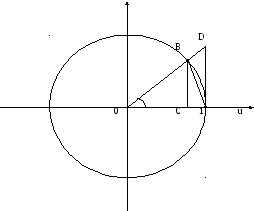
Вычислим площадь
треугольника
 А0В,
сектора
А0В,
сектора
 и △А0D.
и △А0D.
 А0В
А0В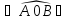 △А0D.
△А0D.
пл.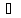 А0В<пл.
А0В<пл.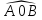 <пл.
△А0D.
<пл.
△А0D.
Из элементарной
геометрии:
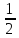 ·1·
·1·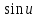 <
<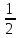 ·1·
·1·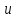 <
<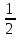 ·1·
tg
·1·
tg
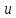
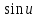 <
< <
tg
<
tg
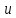 и т.к.
и т.к.
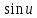 >0,
то 1<
>0,
то 1<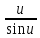 <
<

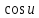 <
< <1.
<1.
 =
=
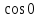 =1
=1
Тогда по теореме о
предельном переходе в неравенствах для
трёх функций
 =1
=1
-


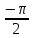 <
< <0
<0
 0<(
0<(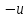 )<
)<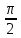

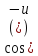 <
<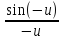 <1.
<1.
Согласно
чётности
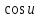 и нечётности
и нечётности
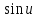 :
:
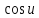 <
<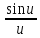 <1.
<1.
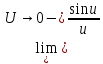 =1
=1
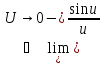 =
=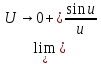 =1
=1
 согласно теореме §5 получаем
согласно теореме §5 получаем
 =1.
=1.
Рассмотрим
g(х)=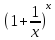 ;
Х=(
;
Х=(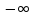 ,
,
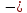 1)
1)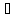 (0,
+
(0,
+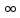 )
)
 стандарстная область определения
функции g(х).
стандарстная область определения
функции g(х).
Докажем,
что
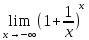 =
=
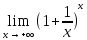 =e.
=e.
Для
этого сначала докажем, что
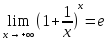

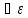 >0
>0
 D>0
D>0
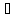 х
(х
х
(х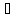 Х,
х>D): │
Х,
х>D): │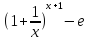 │<
│<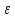 .
.
А так как
g(х)=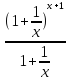 , то
, то
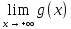 =
= =e
=e
-
Возьмём произвольное
 >0
и зафиксируем его. Ищем
D>0.
>0
и зафиксируем его. Ищем
D>0.
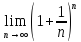 =e
=e
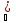
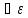 >0,
а значит и для нашего фиксированного
>0,
а значит и для нашего фиксированного
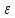 >0
>0
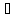 N1
N1
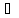 n>
N1:
│
n>
N1:
│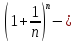 e│<
e│<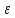 .
.
e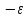 <
<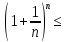 e=sup{
e=sup{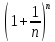 }
(*)
}
(*)
А так как
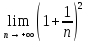 =1
=1
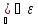 >0,
>0,
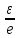 >0,
>0,
 N2
N2
 n>N2:
│
n>N2:
│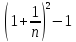 │<
│<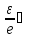 1
1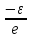 <
<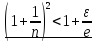
 <1+
<1+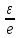 (**)
(**)
Положим N=max{N1, N2}, D=N+1>0.
Тогда
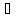 х>D
и
х>D
и
 =n
получаем n
=n
получаем n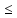 х<n+1
х<n+1
 n>N
n>N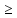 N1
и n>N
N1
и n>N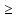 N2
N2
e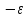 <
<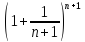 <
< <
<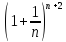 =
=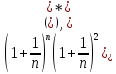 e(1+
e(1+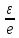 )=e+
)=e+

-
Докажем, что │
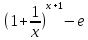 │<
│<
 =e.
=e.
Используем определение (Г)2.
Возьмём произвольную
последовательность {xn}
типа Гейне ( n:
хn
n:
хn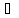 Х
Х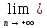 хn=
хn=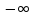 )
и проверим, что
)
и проверим, что
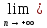 g(х)=e.
g(х)=e.
Так как Х=(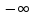 ,
,
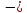 1)
1)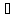 (0,
+
(0,
+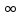 ),
то не ограничивая общности можно считать,
что
),
то не ограничивая общности можно считать,
что
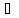 n:
xn<
n:
xn<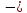 1<0,
то есть xn
1<0,
то есть xn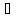 (
(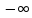 ,
,
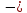 1).
Рассмотрим последовательность {xn’},
где
1).
Рассмотрим последовательность {xn’},
где
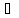 n:
xn’=
n:
xn’= xn>1>0
xn>1>0
 xn’=+
xn’=+ .
.
 n:
g(xn)=
n:
g(xn)=
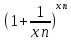 =
=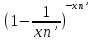 =
=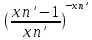 =
=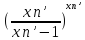 =
=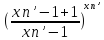 =
=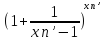 =
=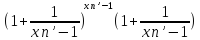 =g(xn’
=g(xn’ 1)
1)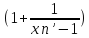
В
силу выбора последовательности {xn},
последовательность {xn 1}
обладает свойствами:
1}
обладает свойствами:
-
 n:
xn’
n:
xn’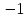 =
=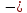 xn
xn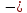 1
1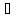 (0,
+
(0,
+ )
)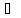 Х
Х -
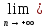 (xn’
(xn’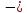 1)=+
1)=+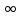 (ибо
(ибо
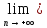 хn=
хn=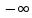 )
)
А тогда по доказанному в п.1
 g(хn)=
g(хn)=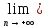 g(xn’
g(xn’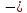 1)
1)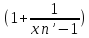 =e.
=e.
А так как последовательность была
выбрана произвольно, то
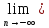 g(хn)
g(хn)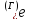 .
.
-
h(z)=
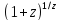 ,
Z==(
,
Z==( ,
0)
,
0)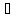 (0,
+
(0,
+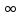 ).
).
Докажем, что
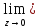 h(z)=
h(z)=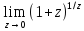 =e.
=e.
Для этого докажем, что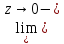 h(z)=
h(z)= h(z)=e.
h(z)=e.
Замечание.
Справедливы следующие утверждения.
Докажите их самостоятельно.
Утверждение 1.
Если
последовательность {yn}
такова, что
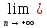 yn=+
yn=+ ,
то последовательность {
,
то последовательность {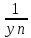 }имеет
смысл, и она бесконечно малая, то есть
}имеет
смысл, и она бесконечно малая, то есть
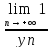 =0.
=0.
Утверждение 2.
Если
последовательность{yn}
такова, что
 n:
yn>0
(
n:
yn>0
(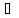 n:
yn<0)
и
n:
yn<0)
и
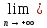 yn=0,
то {
yn=0,
то {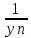 }
бесконечно большая, то есть
}
бесконечно большая, то есть
 (соответственно,
(соответственно,
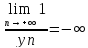 )
)
Вернёмся к функции h(z).
Надо доказать,
что
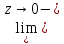 h(z)=e,
h(z)=e,
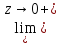 h(z)=e.
h(z)=e.
Возьмём
произвольную последовательность {zn}
такую, что
 n:
zn>0 и
n:
zn>0 и
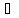 n:
хn=
n:
хn=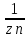 и
и
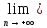 zn=0
zn=0
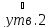
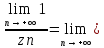 хn=+
хn=+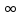 .
.
Рассмотрим
последовательность соответствующих
значений функции h(z):
{h(z)}=
{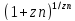 }={
}={ }={g(хn)}.
}={g(хn)}.
Но, следовательно,
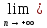 h(zn)=
h(zn)=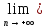 g(хn)=e
g(хn)=e
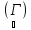
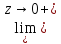 h(z)=e.
h(z)=e.
Аналогично
доказывается, что
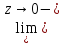 h(z)=e.
h(z)=e.
А тогда из
равенства
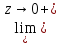 h(z)=
h(z)=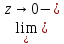 h(z)=e
по теореме §5 следует, что
h(z)=e
по теореме §5 следует, что
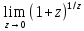 =e.
=e.
Глава 4. Непрерывность функции.
§1. Определение непрерывной функции.
Примеры.
-
f(x)=x2+1,
X=(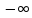 ,
+
,
+ )
)

-
f(x) =
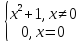
X=(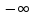 ,
+
,
+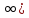

-
f(x)=x2+1,
X=(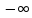 ,
0
,
0 0,
+
0,
+ )
)

-
f(x)=
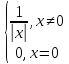
X=(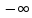 ,
+
,
+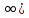

-
f(x)=

X=(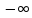 ,
+
,
+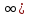

Определение.
Говорят, что функция f(x) со стандартной областью определения X непрерывна в точке xо, если
-
xо
 X
X -
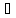
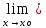 f(x)
f(x) -
 f(x)=
f(xо)
f(x)=
f(xо)
Расшифровка определения непрерывности функции в точке.
I (1). xо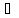 X, (2) - (3) в смысле Гейне
X, (2) - (3) в смысле Гейне
 {хn}
{хn}
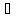 n:
хn
n:
хn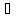 Х
Х
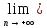 хn=
хо
:
хn=
хо
:
 f(xn)
= f(xо)
f(xn)
= f(xо)
II
(1). xо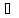 X, (2) – (3) в смысле Коши
X, (2) – (3) в смысле Коши
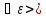 0
0
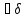 >0
>0
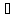 х
(х
х
(х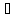 Х,
│x - хо│<
Х,
│x - хо│<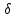 ):
│f(х)- f(xо)│<
):
│f(х)- f(xо)│<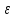
III
Зафиксируем точку xо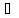 X и возьмём приращение
(смещение) △x
такое, чтобы xо+△x
X и возьмём приращение
(смещение) △x
такое, чтобы xо+△x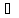 X. Пусть xо+h= xо+△x=x
X. Пусть xо+h= xо+△x=x
 h=△x=x- xо
h=△x=x- xо
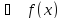 =
f(xо+h)=
f(xо+△x)
=
f(xо+h)=
f(xо+△x)
-
xо
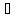 X, (2) – (3) означает, что
X, (2) – (3) означает, что
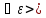 0
0
 >0
>0
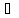 h
(xо+h
h
(xо+h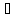 Х,
Х,
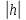 <
< ):
│f(xо+h)
– f(xо)
│<
):
│f(xо+h)
– f(xо)
│<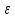

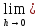 f(xо+△x)=
f(xо)
f(xо+△x)=
f(xо)
IV
Зафиксируем xо X и сместимся из точки xо
в точку x= xо+ △x
X и сместимся из точки xо
в точку x= xо+ △x
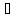 X,
не покидая X.
X,
не покидая X.
Обозначим через △f=△f(xо; △x)= f(xо+△x) –f(xо) – приращение функции, вызванное смещением △x из точки xо.
-
xо
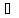 X, (2) – (3):
X, (2) – (3):
 △f
(xо; △x)=
△f
(xо; △x)=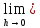 △f(xо;
h)=0.
△f(xо;
h)=0.
Определение.
Функция f(x) называется непрерывной на множестве X, если она непрерывна в каждой точке X.
Определение.
Точка xо называется точкой разрыва функции f(x), если
либо xо X, но является концом
одновременно двух смежных промежутков
из X;
X, но является концом
одновременно двух смежных промежутков
из X;
либо xо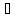 X, но
X, но
 f(x);
f(x);
либо xо X,
X,
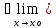 f(x),
но
f(x),
но
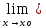 f(x)
f(x) f(xо).
f(xо).
Определение.
Функция f(x) называется непрерывной, если она не имеет точек разрыва как принадлежащих X, так и не принадлежащих X.
Примеры.
-
f(x)=
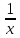 ,
X=(–
,
X=(–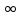 ,
0)
,
0)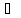 (0,
+
(0,
+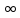 ).
).
f(x) непрерывна на X, но xо=0 – точка разрыва функции f(x).
-
f(x)=
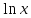 ,
X=(0, +
,
X=(0, + )
)
f(x) непрерывна на X и f(x) непрерывная функция.
-
Докажем сначала, что f(x) непрерывна на X.
Возьмём произвольное x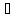 X
и дадим ему приращение △x
такое, чтобы xо+△x
X
и дадим ему приращение △x
такое, чтобы xо+△x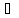 X
X
 △f(x; △x)=
△f(x; △x)=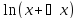 –
–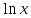 =
=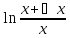 =
=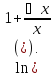 Но
Но
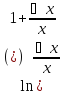 при △x
при △x 0
0
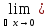 △f(x;
△x)=
△f(x;
△x)=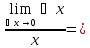 0
0
 По расшифровке IV
По расшифровке IV
 непрерывен в точке x
непрерывен в точке x

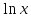 непрерывен на (0, +
непрерывен на (0, +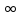 )=X.
)=X.
-
Но точек разрыва у
 нет, следовательно, f(x)=
нет, следовательно, f(x)=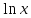 – непрерывная функция.
– непрерывная функция.