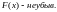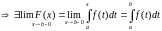Вопрос № 5
Опр : Прямая
 наз-ся
вертикальной асимптотой графика ф-ии
наз-ся
вертикальной асимптотой графика ф-ии
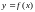 ,
если
,
если
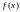 -б.б.
в точке
-б.б.
в точке
 .
.
Опр: Прямая
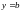 -
наз-ся горизонтальной в асимптотой
гр.ф-ии
,
если
-
наз-ся горизонтальной в асимптотой
гр.ф-ии
,
если
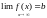
Опр: Прямая
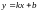 наз-ся
наклонной асимптотой графика ф-ии
,
если
наз-ся
наклонной асимптотой графика ф-ии
,
если 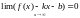
Теорема :
Если
-
наклонная асимптота гр. ф-ии
,
то
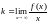 ;
;

Т.к.
 -
наклонная асимптота , то
-
наклонная асимптота , то
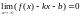
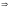
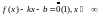
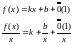
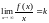
 значит
значит
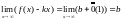
Теорема :
Пусть
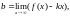 тогда
прямая
-
наклонная асимптота гр.ф-ии
тогда
прямая
-
наклонная асимптота гр.ф-ии
 -наклонная
асимптота
-наклонная
асимптота
Вопрос № 1
Опр: Ф-ия f(x)
наз-ся возрастающей в точке
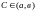 , если
, если
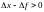 в данной точке, т.е. увеличению
аргумента соответствует увеличение
значения ф-ии , а уменьшению аргумента
уменьшение значения ф-ии .
в данной точке, т.е. увеличению
аргумента соответствует увеличение
значения ф-ии , а уменьшению аргумента
уменьшение значения ф-ии .
Опр: Ф-ия f(x)
наз-ся возрастающей в точке
, если
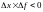 в данной точке , т.е. увеличению
аргумента соответствует уменьшение
значения ф-ии , а уменьшению аргумента
соответствует увеличение значения
ф-ии .
в данной точке , т.е. увеличению
аргумента соответствует уменьшение
значения ф-ии , а уменьшению аргумента
соответствует увеличение значения
ф-ии .
(дорисовать ф-ии )
Опр : Говорят , что
ф-ия f(x)
возрастает ( убывает) на
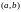 ,
если она возрастает (убывает) в
каждой точке
.
,
если она возрастает (убывает) в
каждой точке
.
Опр: Говорят, что ф-ия f(x) монотонна на ,если она возрастает на , или убывает на
Теорема (Достаточное условие монотонности )
Пусть дана ф-ия
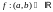 ,
причем
,
причем
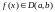
1) Если
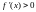 для
для
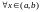 ,
то
- возрастает
,
то
- возрастает
2)Если
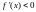 для
,
то
- убывает
для
,
то
- убывает
Докажем 1
Возьмем
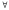
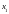 ,
,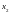
 т.ч.
т.ч.

Без потери общности считается , что < .
По теореме Лагранжа
:
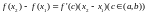
Т.к.
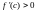 и
и

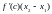 > 0
> 0
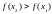 для
>
в-ет
на
для
>
в-ет
на
Вторая теорема о среднем
Теорема
Пусть задана ф-ия
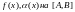 т.ч.
т.ч.
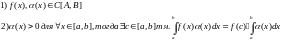

По теореме о
промеж.значениях ф-ии неприрыв.на отрезке
 т.ч.
т.ч.
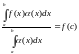
Вопрос 3
Опр : Ф-ия
наз-ся
выпуклой вниз в точке
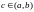 ,
если
,
если
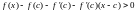 для
для
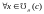
Опр: Ф-ия наз-ся выпуклой вверх в точке , если
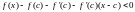 для
для
Опр : Говорят , что ф-ия выпуклая вверх(вниз) на , если она выпукла вверх(вниз) в каждой точке
Теорема(достаточное условие выпуклости) :
Пусть дана ф-ия
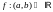 причем
причем
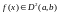
1) Если
 для
для
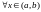 ,
то
-выпуклая
вниз на
,
то
-выпуклая
вниз на
2)Если
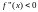 для
,
то
-выпуклая
вверх на
для
,
то
-выпуклая
вверх на
 Д-ем
пункт 1
Д-ем
пункт 1
Воспользуемся формулой Тейлора :
Пусть .
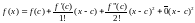
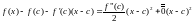
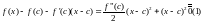
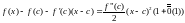 для
для
Следовательно
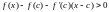 для
для
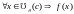 -
выпуклая вниз в точке
-
выпуклая вниз в точке
 .
.
-выпуклая вниз на
Длина дуги кривой , заданной графиком функции (31)
Опр : Пусть даны
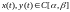 тогда
соответствующий кривой наз-ся мн-во
точек вида :
тогда
соответствующий кривой наз-ся мн-во
точек вида :

При этом
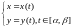 -параметризация
данной кривой
-параметризация
данной кривой
*рисунок*
Теорема
Пусть
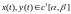 .
Р-м кривую
.
Р-м кривую
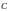 с
параметризацией
тогда
с
параметризацией
тогда
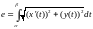
Без док-ва
Кривые, заданные в
полярных координатах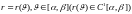
*рисунок*
Теорема :
Если
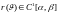 то
то
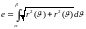
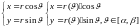 по
доказанной теореме :
по
доказанной теореме :
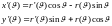
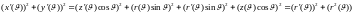
Доказательства формулы для вычисления площади (29)
Опр: Пусть ф-ия
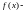 определена
на
определена
на
 причем
причем
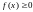 для
для
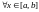 тогда
в соответ. криволенийной трапеции наз-ся
:
тогда
в соответ. криволенийной трапеции наз-ся
:
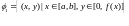
*рисунок*
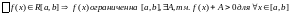
Параллельно переносим фигуру Ф на А единиц вверх:
*рисунок*
Достаточные условия дифференцируемости функции (48)
Теорема
Пусть у ф-ии
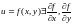 в
некоторой окр-ти точки
в
некоторой окр-ти точки
 ,
причем
,
причем

Теорема
Пусть


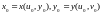 ,
тогда сложная ф-ия
,
тогда сложная ф-ия
 причем
причем
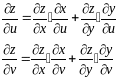
Достаточные условия интегрирования (19)
Теорема
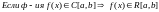
без док-ва
Евклидов n-мерное пространство (40)
Опр:
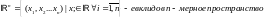
Опр: Пусть
 то
расстояние от
то
расстояние от
 до
до
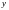 наз-ся
наз-ся
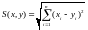
Опр: Открытым шагом
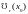 с
центром в точке
с
центром в точке
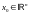 и
радиуса
и
радиуса
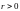 наз-ся
наз-ся
 *рисунок*
*рисунок*
Опр: Множество
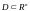 наз-ся
открытым, если для
наз-ся
открытым, если для
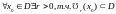
Опр: Точка
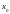 наз-ся предельной точкой мн-ва
наз-ся предельной точкой мн-ва
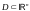 если
для
если
для

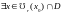
Опр: Мн-во наз-ся замкнутой, если оно содержит все свои прдельные точки
Опр: Точка наз-ся граничной точкой мн-ва , если для содержит как принадлеж. D точку, так и на принадлеж.
Опр: Гранцей мн-ва наз-ся мн-во всех его гранитных точек
Опр: Замыканием мн-ва
наз-ся
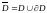
Опр: Мн-во
наз-ся связным , если для
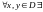 непрерывная
кривая
непрерывная
кривая
 ,
т.к. 1)
,
т.к. 1)
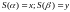
2)

Опр: Мн-во наз-ся областью, если оно открыто и связано
Интеграл с переменным верхним пределом (24)
Пусть
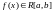 тогда
тогда
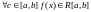 след-но
определена ф-ия
след-но
определена ф-ия
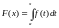 -
называется интегралом с переменным
верхнем пределом.
-
называется интегралом с переменным
верхнем пределом.
Теорема :
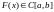
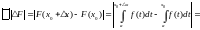
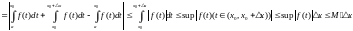
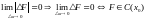 т.к.
т.к.
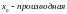 .
.
Вопрос № 15
Интегралы от ф-ии вида
 ,где
,где
 -рац.ф-ия
-рац.ф-ия
Замена:
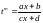 получается
интеграл от рац.дроби
получается
интеграл от рац.дроби
Пример:
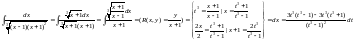
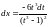
=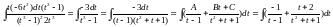 =
=
= =
=
=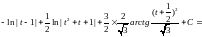 обратная
замена
обратная
замена
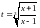
Вопрос № 16
Дифференциальный
бином - это выражение вида
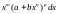
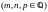
1случай
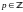 ,
тогда замена
,
тогда замена
 ,
где
,
где
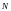 -общей
знаменатель . Тогда замена сведет
вычисление интеграла к интегралу от
рац.чисел
-общей
знаменатель . Тогда замена сведет
вычисление интеграла к интегралу от
рац.чисел
2 случай
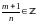 ,
тогда замена
,
тогда замена
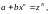 где
-знаменатель
где
-знаменатель
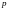 .Тогда
замена интегралу от рац.чисел
.Тогда
замена интегралу от рац.чисел
3 случай
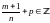 ,
тогда замена :
,
тогда замена :
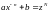 ,
где
-знаменатель
.
,
где
-знаменатель
.
Замечание
В остальных случаях интегралы в элементарных функциях на берется (теорема Чебылева)
Критерий сходимости несобственного интеграла (36)
Теорема :
Пусть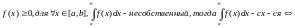
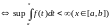
 Рассмотрим
первообразную
Рассмотрим
первообразную
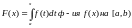
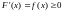 для
для
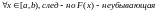
Предположим,
что
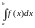 -сх-ся,
т.к.
-сх-ся,
т.к.
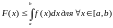
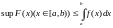
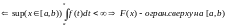 более
того
более
того