- •Глава I. Действительные числа.
- •§1. Введение.
- •§2. Множества.
- •§3. Понятие множества действительных чисел.
- •§4. Отображения множеств.
- •Глава 2. Числовые последовательности.
- •§1. Понятие числовой последовательности.
- •§2. Бесконечно малые последовательности.
- •§3. Свойства сходящихся последовательностей.
- •Глава 3. Некоторые сведения из математической логики.
- •§1. Предложение.
- •§2. Предикаты.
- •§3. Кванторы.
- •§4. Предельный переход в неравенствах. (Глава 2)
- •§5. Бесконечно большие последовательности.
- •§6. Частичные последовательности (подпоследовательности).
- •§7. Монотонные последовательности.
- •§8. Теорема о вложенных отрезках.
- •§9. Теорема Больцано-Вейерштрасса.
- •§10. Критерий Коши сходимости числовой последовательности.
- •§11. Число .
- •Глава 3. Функции.
- •§1. Понятие числовой функции числового аргумента.
- •§2. Предел функции в точке.
- •§3. Арифметические свойства пределов функций.
- •§4. Предельный переход в неравенствах.
- •§5. Односторонние пределы функции в точке. (пределы слева и справа)
- •§6. Пределы функций на бесконечности.
- •§7. Функции, стремящиеся к бесконечности. (Бесконечно большие функции.)
- •§8. Сравнение бесконечно малых и бесконечно больших функций.
- •§9. Специальные пределы функций.
- •Глава 4. Непрерывность функции.
- •§1. Определение непрерывной функции.
- •§2. Классификация точек разрыва функции.
- •§3. Простейшие свойства непрерывных функций.
- •§4. Некоторые свойства непрерывных функций на промежутке.
- •§5. Условия непрерывности монотонной функции. Обратная функция. Непрерывность обратной функции.
- •Глава 5. Производная функции.
- •§1. Понятие производной функции.
- •§2. Свойства производной функции.
- •§3. Производная обратной функции.
- •§4. Таблица производных.
- •Глава 6. Дифференцируемая функция. Дифференциал.
- •§1. Понятие дифференцируемой функции в точке и дифференциала.
- •§2. Некоторые свойства дифференциала функции в точке.
Глава I. Действительные числа.
§1. Введение.
Математический анализ – это классическая часть современной геометрии. Развитие именно современной геометрии началось с публикации Н.И.Лобачевского¹ работы «О началах геометрии» 1829, в которой была решена проблема V постулата Евклида о параллельных. Н.И.Лобачевский доказал, что V постулат Евклида не вытекает из остальных постулатов и поэтому возможна другая геометрия. Он назвал её воображаемой, а мы сейчас называем её неевклидовой или геометрией Лобачевского. Первое сообщение было сделано 23.02.1826 г. В Казанском Университете.
Открытие Лобачевского:
-
Лишило всякого смысла мысль о врождённости геометрических (понятий) объектов;
-
Заставило глубже вникнуть в смысл геометрических понятий;
-
Чрезвычайно важным оказалось осознание того факта, что логическая структура геометрии не определяет природы геометрических объектов.
Это означает, что в качестве „точек”, „прямых”, „плоскостей” в разных случаях можно подразумевать разные предметы (объекты).
Каждый конкретный выбор этих объектов даёт конкретную „модель” геометрии.
§2. Множества.
С конца 19 века наиболее универсальным языком математики стал язык теории множеств. Основателем теорий множеств является немецкий математик Георг Кантор². Кантор говорил: „… под множеством мы понимаем объединение в одно целое определённых объектов, вполне различных, нашей интуиции или нашей мысли”. На рубеже 19-го и 20-го веков на Конгрессе математиков в 1900 году отмечалось, какую огромную пользу принёс теоретико-множественный язык для развития математики.
А в 1902 году Б. Рассел³ обнаружил парадокс, оказавшийся классическим парадоксом, схожим с парадоксом Зенона (например, о брадобрее). Оказалось, что высказывание – “множество всех множеств” – противоречиво.
Если в теории, где-то противоречие, то как же пользоваться её результатами? Опасно! Значит, наивное представление о множестве не так уже просто и безобидно. Высказывание Кантора трудно принять за определение. Поэтому логики подвергают понятие множества тщательному анализу, в который мы углубляться не будем.
Заметим, что в существующих аксиоматических теориях множество определяется как математический объект, обладающий определённым набором свойств. Описание этих свойств составляет аксиоматику. Любая из существующих аксиоматик такова, что она с одной стороны избавляет от известных противоречий наивной теории множеств, а с другой стороны – обеспечивает свободу оперирования с конкретными множествами, возникающими в различных отделах математики и в первую очередь в математическом анализе (в широком смысле слова – как современной геометрии).
X – множество; x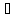 X
– x элемент множества X.
X
– x элемент множества X.
Определение.
Множество, не содержащее элементов,
называется пустым множеством и
обозначается
 .
.
Определение.
Множество А называется конечным, если оно состоит из конечного числа элементов.
Определение.
Пусть даны два множества А и В. А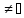 ,
В
,
В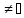 и пусть каждый элемент x
и пусть каждый элемент x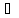 А
является элементом множества В, т.е.
x
А
является элементом множества В, т.е.
x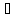 В.
Тогда А называется подмножеством
множества В, обозначается А
В.
Тогда А называется подмножеством
множества В, обозначается А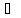 В.
В.
Замечание.
Для любого множества А, А≠ ,
следует А
,
следует А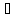 А
(из определения).
А
(из определения).
Определение.
Пусть X – произвольное множество. X и
 называются несобственными
подмножествами множества X.
называются несобственными
подмножествами множества X.
Определение.
Пусть X – непустое множество и А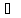 X,
А
X,
А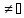 и пусть существует x
и пусть существует x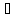 X
такой, что x
X
такой, что x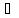 А.
Тогда А называется собственным
подмножеством множества X.
А.
Тогда А называется собственным
подмножеством множества X.
Простейшие операции над множествами.
Пусть X – произвольное непустое множество
и А X.
X.
Определение.
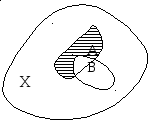
Разностью между множествами А и В
называется множество, обозначаемое А В
либо пустое, либо состоящее из тех
элементов множества А, которые не
принадлежат множеству В.
В
либо пустое, либо состоящее из тех
элементов множества А, которые не
принадлежат множеству В.
Определение.
Пусть А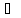 X.
Дополнением множества А в X называется
X
X.
Дополнением множества А в X называется
X А.
оно обозначается СхА=СА= X
А.
оно обозначается СхА=СА= X А.
А.
Пусть задана совокупность множества Аα, где {α}=y – совокупность индексов.
Определение.
Объединением
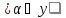 Аα множеств Аα, α
Аα множеств Аα, α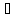 y
называется множество, каждый элемент
которого (если он существует) принадлежит
хотя бы одному Аα, т.е. либо
y
называется множество, каждый элемент
которого (если он существует) принадлежит
хотя бы одному Аα, т.е. либо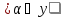 Аα =
Аα = ,
либо условие x
,
либо условие x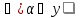 Аα равносильно условию –
существует α
Аα равносильно условию –
существует α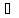 y
такое, что x
y
такое, что x Аα.
Аα.
Определение.
Пересечением множеств Аα,
α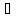 y,
называется множество, каждый элемент
которого (если он существует) принадлежит
каждому множеству Аα, α
y,
называется множество, каждый элемент
которого (если он существует) принадлежит
каждому множеству Аα, α y.
Обозначается пересечение множеств Аα,
α
y.
Обозначается пересечение множеств Аα,
α y
через
y
через
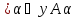 .
.
Задача.
Доказать, что если X – непустое множество
и для всех α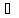 y
Аα
y
Аα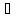 X,
то
X,
то
-
X
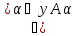 )=
)= (1) Сх
(1) Сх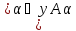 )=
)=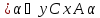
-
X
 (
(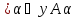 )=
)=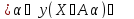 (2) Сх(
(2) Сх(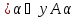 )=
)=