- •Глава I. Действительные числа.
- •§1. Введение.
- •§2. Множества.
- •§3. Понятие множества действительных чисел.
- •§4. Отображения множеств.
- •Глава 2. Числовые последовательности.
- •§1. Понятие числовой последовательности.
- •§2. Бесконечно малые последовательности.
- •§3. Свойства сходящихся последовательностей.
- •Глава 3. Некоторые сведения из математической логики.
- •§1. Предложение.
- •§2. Предикаты.
- •§3. Кванторы.
- •§4. Предельный переход в неравенствах. (Глава 2)
- •§5. Бесконечно большие последовательности.
- •§6. Частичные последовательности (подпоследовательности).
- •§7. Монотонные последовательности.
- •§8. Теорема о вложенных отрезках.
- •§9. Теорема Больцано-Вейерштрасса.
- •§10. Критерий Коши сходимости числовой последовательности.
- •§11. Число .
- •Глава 3. Функции.
- •§1. Понятие числовой функции числового аргумента.
- •§2. Предел функции в точке.
- •§3. Арифметические свойства пределов функций.
- •§4. Предельный переход в неравенствах.
- •§5. Односторонние пределы функции в точке. (пределы слева и справа)
- •§6. Пределы функций на бесконечности.
- •§7. Функции, стремящиеся к бесконечности. (Бесконечно большие функции.)
- •§8. Сравнение бесконечно малых и бесконечно больших функций.
- •§9. Специальные пределы функций.
- •Глава 4. Непрерывность функции.
- •§1. Определение непрерывной функции.
- •§2. Классификация точек разрыва функции.
- •§3. Простейшие свойства непрерывных функций.
- •§4. Некоторые свойства непрерывных функций на промежутке.
- •§5. Условия непрерывности монотонной функции. Обратная функция. Непрерывность обратной функции.
- •Глава 5. Производная функции.
- •§1. Понятие производной функции.
- •§2. Свойства производной функции.
- •§3. Производная обратной функции.
- •§4. Таблица производных.
- •Глава 6. Дифференцируемая функция. Дифференциал.
- •§1. Понятие дифференцируемой функции в точке и дифференциала.
- •§2. Некоторые свойства дифференциала функции в точке.
§4. Отображения множеств.
Определение.
Пусть X
и Y два непустых множества.
Говорят, что задано отображение f
множества X „в” множество
Y, если указан закон,
согласно которому элементу x поставлен в соответствие элемент
y
поставлен в соответствие элемент
y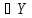 .
.
Обозначение
f: X Y; X
Y; X Y.
Y.
Если y=f(x),
x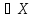 ,
y
,
y ,
то y называется образом
x при отображении f, а x при
этом называется прообразом y
при отображении f.
,
то y называется образом
x при отображении f, а x при
этом называется прообразом y
при отображении f.
Множество
Yf
= {y; y=f(x),
x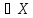 }
} Y
называется образом множества X при
отображении f.
Y
называется образом множества X при
отображении f.
Определение.
Говорят, что
два непустых множества X и Y равны,
если каждый элемент x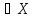 принадлежит Y (X
принадлежит Y (X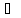 Y)
и каждый элемент y
Y)
и каждый элемент y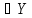 принадлежит X (Y
принадлежит X (Y X),
то есть
X),
то есть
X=Y X
X Y
и Y
Y
и Y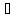 X.
X.
Определение.
Говорят, что задано отображение f множества X „на” множество Y, если Yf =Y.
Определение.
Отображение
f: X Y называется взаимно-однозначным,
если разным x из X ставятся в
соответствие разные y из Y.
Y называется взаимно-однозначным,
если разным x из X ставятся в
соответствие разные y из Y.
Определение.
Говорят, что два непустых множества X и Y являются равномощными, если между ними можно установить взаимно-однозначное отображение.
Определение.
Множество,
равномощное множеству
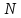 натуральных чисел называется счётным.
натуральных чисел называется счётным.
Определение.
Бесконечное множество, не являющееся счетным, называется несчётным.
Утверждение 1. (Доказать самостоятельно).
Любое бесконечное множество содержит счётное подмножество.
Утверждение 2. (Доказать самостоятельно).
Любое бесконечное подмножество счётного множества счётно.
Теорема 1.
Множество
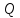 всех рациональных чисел счётно.
всех рациональных чисел счётно.
Доказательство.
Рассмотрим
множество
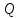 всех рациональных чисел и расположим
их следующим образом:
всех рациональных чисел и расположим
их следующим образом:
0 1 -1 2 -2 3 -3 …
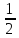 -
-
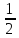
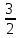 -
-

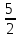 -
-
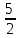
 …
…
 -
-
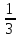
 -
-

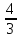 -
-


… … …
Отметим место каждого числа.
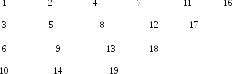


Теорема 2. (Кантора). (Без доказательства).
Множество
 действительных чисел несчётно.
действительных чисел несчётно.
Задача.

 Где больше чисел?
Где больше чисел?
§ Точные
грани (верхняя и нижняя) числовых
множеств.
Точные
грани (верхняя и нижняя) числовых
множеств.
Примеры.
X=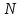 ={1,
2, …, n, n+1, …}
={1,
2, …, n, n+1, …}
X ={x;
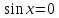 }
}
X=
(-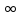 ,
+
,
+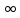 )
)
X={r; r – рационально: r2<2}
Определение.
Числовое
множество X называется ограниченным
сверху (снизу), если существует такое
число В (соответственно А), что для любого
x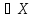 :
x
:
x В
(соответственно А
В
(соответственно А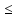 x).
x).
Определение.
Числовое множество X называется ограниченным, если оно ограниченно и сверху и снизу.
Определение.
Пусть X – ограниченное сверху числовое множество. Точной верхней гранью множества X называется наименьшее из всех чисел, ограничивающих множество X сверху, и оно обозначается supX= sup{x}.
Определение.
Пусть X – ограниченное снизу числовое множество. Точной нижней гранью множества X называется наибольшее из всех чисел, ограничивающих множество X снизу. Оно обозначается infX=inf{x}.
Дадим рабочую форму этих понятий.
Определение.
Пусть X – ограниченное сверху числовое множество. Число M= supX называется точной верхней гранью множества X, если:
-
для любого x
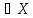 :
x
:
x M.
M. -
для каждого
 >0
существует
>0
существует
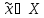 такой, что M-
такой, что M-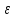 <
< .
.
Определение.
Пусть X – ограниченное снизу числовое множество. Число m= infX называется точной нижней гранью множества X, если:
-
для любого x
 :
m
:
m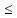 x.
x. -
для каждого
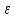 >0
существует
>0
существует
 такой, что
такой, что
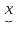 <m+
<m+ .
.
Иногда
случается, что числовое множество X
имеет наибольший (наименьший) элемент,
т.е. существует
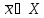 (соответственно
(соответственно
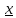 )
такой, что для любого x
)
такой, что для любого x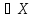 :
x
:
x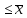 (соответственно x
(соответственно x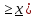 .
.
Утверждение.
Пусть
 - наибольший элемент множества X. Тогда
- наибольший элемент множества X. Тогда
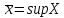 .
.
Доказательство.
Воспользуемся рабочей формулой определения точной верхней грани множества X.
Проверим выполнение двух условий.
-
По определению наибольшего элемента для любого x
 :
x
:
x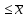 .
. -
Возьмём произвольное
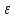 >0,
фиксируем его.
>0,
фиксируем его.
Тогда
 ,
а
,
а
 .
.
Утверждение для наименьшего элемента докажите самостоятельно.
Теорема 1. (О существовании точной верхней грани у ограниченного сверху числового множества)
Любое непустое ограниченное сверху числовое множество имеет точную верхнюю грань.
Доказательство.
Пусть X ,
X
,
X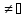 и существует В такое, что для любого x
и существует В такое, что для любого x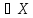 :
x
:
x В.
В.
Рассмотрим множество E всех чисел, ограничивающих множество X сверху.
E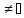 ,
так как В
,
так как В E.
Следовательно, мы имеем два множества
X и E, обладающих свойством:
E.
Следовательно, мы имеем два множества
X и E, обладающих свойством:
X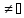 ,
E
,
E и для каждого x
и для каждого x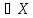 и для каждого В
и для каждого В E
x
E
x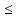 В.
В.
А тогда
согласно аксиоме V (полноты и непрерывности)
множества
 действительных чисел существует Во
действительных чисел существует Во такое, что для любого x
такое, что для любого x и для любого В
и для любого В E
E
x Во
Во В.
В.
Из левой
части неравенства x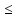 Во следует, что для любого x
Во следует, что для любого x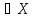 :
x
:
x Во
Во
 Во ограничивает множество
X сверху
Во ограничивает множество
X сверху
 Во
Во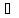 E.
E.
Из правой
части неравенства следует, что для
любого В E:
Во
E:
Во В,
а так как Во
В,
а так как Во E,
то Во – наименьшее из чисел,
ограничивающих множество X сверху
E,
то Во – наименьшее из чисел,
ограничивающих множество X сверху

Во= supX.
Доказательство, приведённое выше, принадлежит М.А.Крейнесу.
Теорема 2. (О существовании точной нижней грани у ограниченного снизу числового множества).
Любое непустое ограниченное снизу числовое множество имеет точную нижнюю грань.
Доказательство.
Пусть
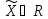 ,
,
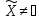 и
и
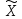 – ограниченно снизу, то есть существует
А такое, что для любого x
– ограниченно снизу, то есть существует
А такое, что для любого x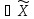 :
А
:
А x.
x.
Рассмотрим
множество X={-x; x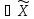 }.
Тогда для любого -x
}.
Тогда для любого -x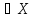 :
- x
:
- x -А,
то есть множество X ограничено сверху
и согласно теореме 1 существует Во=
supX
-А,
то есть множество X ограничено сверху
и согласно теореме 1 существует Во=
supX
 для
любого x
для
любого x :
x
:
x Во
Во
 -x
-x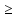 -
Во
-
Во
 - Во=inf
- Во=inf