
- •Глава I. Действительные числа.
- •§1. Введение.
- •§2. Множества.
- •§3. Понятие множества действительных чисел.
- •§4. Отображения множеств.
- •Глава 2. Числовые последовательности.
- •§1. Понятие числовой последовательности.
- •§2. Бесконечно малые последовательности.
- •§3. Свойства сходящихся последовательностей.
- •Глава 3. Некоторые сведения из математической логики.
- •§1. Предложение.
- •§2. Предикаты.
- •§3. Кванторы.
- •§4. Предельный переход в неравенствах. (Глава 2)
- •§5. Бесконечно большие последовательности.
- •§6. Частичные последовательности (подпоследовательности).
- •§7. Монотонные последовательности.
- •§8. Теорема о вложенных отрезках.
- •§9. Теорема Больцано-Вейерштрасса.
- •§10. Критерий Коши сходимости числовой последовательности.
- •§11. Число .
- •Глава 3. Функции.
- •§1. Понятие числовой функции числового аргумента.
- •§2. Предел функции в точке.
- •§3. Арифметические свойства пределов функций.
- •§4. Предельный переход в неравенствах.
- •§5. Односторонние пределы функции в точке. (пределы слева и справа)
- •§6. Пределы функций на бесконечности.
- •§7. Функции, стремящиеся к бесконечности. (Бесконечно большие функции.)
- •§8. Сравнение бесконечно малых и бесконечно больших функций.
- •§9. Специальные пределы функций.
- •Глава 4. Непрерывность функции.
- •§1. Определение непрерывной функции.
- •§2. Классификация точек разрыва функции.
- •§3. Простейшие свойства непрерывных функций.
- •§4. Некоторые свойства непрерывных функций на промежутке.
- •§5. Условия непрерывности монотонной функции. Обратная функция. Непрерывность обратной функции.
- •Глава 5. Производная функции.
- •§1. Понятие производной функции.
- •§2. Свойства производной функции.
- •§3. Производная обратной функции.
- •§4. Таблица производных.
- •Глава 6. Дифференцируемая функция. Дифференциал.
- •§1. Понятие дифференцируемой функции в точке и дифференциала.
- •§2. Некоторые свойства дифференциала функции в точке.
§2. Предел функции в точке.
Определение.
Пусть f(х) – функция, имеющая стандартную область определения Х, хо – фиксированная точка, лежащая внутри или являющаяся концом одного из промежутков, образующих Х.
Говорят,
что f(х) имеет предел в т. хо,
равный L и пишут
 f(х)=L,
если:
f(х)=L,
если:
(Г) (в смысле Гейне) (К) (в смысле Коши)
 {хn}:
1.
{хn}:
1.
 n:
хn
n:
хn Х
Х
 0
0
 >0
>0
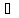 х
х
 n:
хn
n:
хn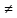 хо
:
хо
: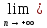 f(хn)=L
х
f(хn)=L
х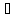 Х
Х
3. хn=
хо
х
хn=
хо
х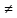 хо
: │f(х)- L│<
хо
: │f(х)- L│<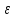

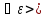 0
0
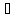 N
N
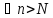 :
│f(хn)-L│<
:
│f(хn)-L│< │x -
хо│<
│x -
хо│<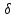
Теорема.
Определения
(Г) и (К) эквивалентны ( (Г)
 (К) ).
(К) ).
Доказательство.
1). (К)
 (Г).
(Г).
Дано: L является пределом функции f(х) в точке хо в смысле Коши.
Докажем, что число L является пределом функции f(х) в точке хо и в смысле Гейне.
Возьмём произвольную последовательность {хn}, удовлетворяющую условиям:
-
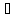 n:
хn
n:
хn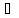 Х
Х -
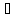 n:
хn
n:
хn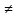 хо
(последовательность типа Гейне)
хо
(последовательность типа Гейне) -
 хn=
хо
хn=
хо
И рассмотрим последовательность соответствующих значений функции f(х): {f(хn)}.
х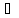 Х
Х
Так
как L=(К)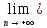 f(х)
f(х)

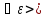 0
0
 >0
>0
 х
х
х
х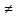 хо
: │f(х)- L│<
хо
: │f(х)- L│<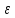 .
│x -
хо│<
.
│x -
хо│<
Возьмём
произвольное
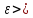 0
и возьмём
0
и возьмём
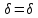 (
( )>0,
которое для
)>0,
которое для
 >0
существует по определению Коши.
>0
существует по определению Коши.
Так
как
 хn=
хо
хn=
хо
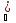
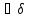 >0,
а значит и для
>0,
а значит и для
 (
( )>0
)>0
 N=N(
N=N(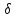 (
(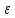 ))
))
 n>N:
│x - хо│<
n>N:
│x - хо│<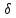 .
Тогда │f(хn)-
L│<
.
Тогда │f(хn)-
L│<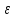

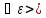 0
0
 N
N
 n>N:
│f(хn)-
L│<
n>N:
│f(хn)-
L│<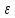

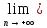 f(хn)=L
f(хn)=L
 так как {хn}
была выбрана произвольно:
так как {хn}
была выбрана произвольно:
 f(х)=(Г)L.
f(х)=(Г)L.
2).
(Г)
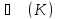 .
.
Дано:
L=(Г) f(х).
f(х).
Докажем,
что L=(К)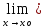 f(х)
f(х)

 0
0
 >0
>0
 х
(х
х
(х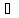 Х,
х
Х,
х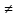 хо,
│x - хо│<
хо,
│x - хо│< )
: │f(х)- L│<
)
: │f(х)- L│<
Пусть L(К)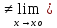 f(х)
f(х)

 о>0
о>0
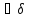 >0
>0
 х′
(х′
х′
(х′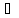 Х,
х′
Х,
х′ хо,
│x′ - хо│<
хо,
│x′ - хо│<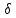 ):
│f(х′)- L│
):
│f(х′)- L│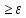 о
о
Тогда
для
 1=1>0
1=1>0
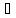 х1′
(х1′
х1′
(х1′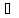 Х,
х1′
Х,
х1′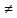 хо,
│x1′ -
хо│<
хо,
│x1′ -
хо│< 1=1):
│f(х1′)-
L│
1=1):
│f(х1′)-
L│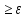 о
о
для
 2=
2=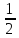 >0
>0
 х2′
(х2′
х2′
(х2′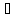 Х,
х2′
Х,
х2′ хо,
│x2′ -
хо│<
хо,
│x2′ -
хо│<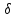 2=
2= ):
│f(х2′)-
L│
):
│f(х2′)-
L│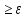 о
о
..........................................................................................................................................
для
 n=
n=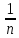 >0
>0
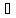 хn′
(хn′
хn′
(хn′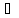 Х,
хn′
Х,
хn′ хо,
│xn′
- хо│<
хо,
│xn′
- хо│<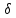 n=
n=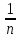 ):
│f(хn′)-
L│
):
│f(хn′)-
L│ о
о
…………………………………………………………………………………………………...
Мы построили последовательность {х′n} такую, что:
-
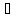 n:
х′
n:
х′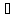 Х,
2)
Х,
2)
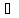 n:
х′
n:
х′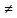 хо,
3)
хо,
3)
 n:
│x′n
- хо│<
n:
│x′n
- хо│<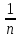
Покажем, что
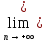 хо
хо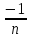 )=
)=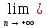 (хn+
(хn+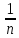 )=
хо.
)=
хо.
А тогда по теореме о
предельном переходе в неравенствах для
трёх последовательностей:
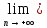 x′n=
хо.
x′n=
хо.
И для {f(х′n)} │f(хn′)-
L│
│f(хn′)-
L│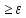 о
о
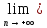 f(хn′)
f(хn′)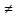 L.
L.
Мы получили ( )
)
 (
( )
)

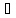 {х′n}
{х′n}
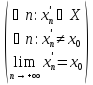 : │f(хn′)-
L│
: │f(хn′)-
L│ о
о
Следовательно, (Г) (К).
(К).
§3. Арифметические свойства пределов функций.
Теорема 1.
Пусть f1(х)
и f2(х) имеют общую стандартную
область определения Х, точка хо
лежит внутри или является концом одного
из промежутков, образующих Х, и L1= f1(х),
L2=
f1(х),
L2=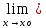 f2(х).
f2(х).
Тогда в точке хо имеет предел и функция f1(х)+ f2(х) и он равен L1+ L2.
Теорема 2.
Пусть f1(х)
и f2(х) имеют общую стандартную
область определения Х, точка хо
лежит внутри или является концом одного
из промежутков, образующих Х, и пусть
L1=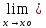 f1(х),
L2=
f1(х),
L2=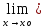 f2(х).
f2(х).
Тогда функция
f1(х)· f2(х) имеет в точке хо
предел
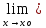 f1(х)·
f2(х) и он равен L1·
L2.
f1(х)·
f2(х) и он равен L1·
L2.
Теорема 3.
Пусть f1(х)
и f2(х) имеют общую стандартную
область определения Х, точка хо
лежит внутри или является концом одного
из промежутков, образующих Х, и пусть
L1= f1(х),
L2=
f1(х),
L2= f2(х),
L2
f2(х),
L2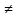 0.
0.
Тогда частное
двух функций
 в точке хо
имеет предел, он равен
в точке хо
имеет предел, он равен
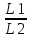 .
.
Доказательство всех трёх теорем проводится с использованием определения предела функции в точке хо в смысле Гейне и арифметических свойств сходящихся последовательностей.
Докажем теорему 2.
Доказательство теоремы 2.
Рассмотрим
функцию f1(х)· f2(х) на Х и
возьмём произвольную последовательность
{хn}
типа Гейне ( n:
хn
n:
хn Х,
Х,
 n:
хn
n:
хn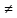 хо,
хо,
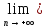 хn=
хо)
и соответствующую последовательность
значений функций f1(хn)·
f2(хn).
хn=
хо)
и соответствующую последовательность
значений функций f1(хn)·
f2(хn).
А так как по
условию теоремы
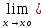 f1(х)=
L1
f1(х)=
L1
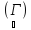
 {хn},
а значит и для нашей {хn}
(
{хn},
а значит и для нашей {хn}
( n:
хn
n:
хn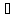 Х,
Х,
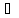 n:
хn
n:
хn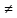 хо,
хо,
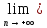 хn=
хо):
хn=
хо):
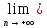 f1(хn)=
L1,
f1(хn)=
L1,
 f2(х)=
L2
f2(х)=
L2
 {хn},
а значит и для нашей {хn}:
{хn},
а значит и для нашей {хn}:
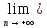 f2(хn)=
L2.
f2(хn)=
L2.
А тогда по теореме о произведении двух сходящихся последовательностей:
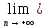 f1(хn)·
f2(хn)=
f1(хn)·
f2(хn)=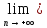 f1(хn)·
f1(хn)· f2(хn)=
L1·L2
f2(хn)=
L1·L2
 так как {хn}
была вфбрана произвольно, то
так как {хn}
была вфбрана произвольно, то
 f1(х)·
f2(х)= L1·L2.
f1(х)·
f2(х)= L1·L2.
Теорема 4.
Пусть f(х) имеет стандартную область определения Х, хо лежит внутри или является концом одного из промежутков, образующих Х, и пусть f(х) в точке хо имеет предел L. Тогда он единственен.
Доказательство.
Пусть
L=(Г) f(х).
Утверждение теоремы непосредственно
следует из определения предела функции
в точке в смысле Гейне и единственности
предела сходящейся последовательности.
f(х).
Утверждение теоремы непосредственно
следует из определения предела функции
в точке в смысле Гейне и единственности
предела сходящейся последовательности.
Теорема 5.
Пусть f(х)
имеет стандартную область определения
Х, хо
лежит внутри или является концом одного
из промежутков, образующих Х. f(х) в точке
хо
имеет предел L
 когда f(х) представима в виде
когда f(х) представима в виде
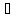 х
х Х:
f(х)=L+
Х:
f(х)=L+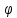 (х),
где
(х),
где
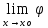 (х)=0.
(х)=0.
Доказательство.
-
Необходимость.
Пусть
 f(х)=
L. Обозначим f(х)- L =
f(х)=
L. Обозначим f(х)- L = (х)
(х)

 х
х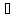 Х:
f(х)= L+
Х:
f(х)= L+ (х).
(х).
Докажем, что
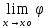 (х)=0.
(х)=0.
Действительно,
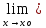 f(х)=(К)
L
f(х)=(К)
L
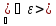 0
0
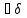 >0
>0
 х
(
х
( х
х Х,
х
Х,
х хо,
хо, │x
- хо│<
│x
- хо│< ):
│
):
│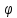 (х)│=│f(х)-
L│<
(х)│=│f(х)-
L│<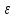

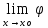 (х)=0.
(х)=0.
-
Достаточность.
Дано: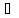 х
х Х:
f(х)= L+
Х:
f(х)= L+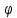 (х),
где
(х),
где
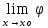 (х)=0.
(х)=0.
Докажем, что
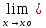 f(х)=
L.
f(х)=
L.
По условию,
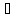 х
х Х:
f(х)= L+
Х:
f(х)= L+ (х),
то
(х),
то
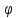 (х)=
f(х)- L
(х)=
f(х)- L
и т.к.
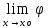 (х)=0
(х)=0

 0
0
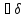 >0
>0
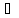 х
(
х
( х
х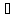 Х,
х
Х,
х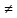 хо,
хо, │x
- хо│<
│x
- хо│< ):
│
):
│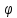 (х)│=
│f(х)- L│<
(х)│=
│f(х)- L│<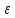

 f(х)=
L.
f(х)=
L.
Теорема 6. (об устойчивости знака функции, имеющей в точке предел)
Пусть
f(х) имеет стандартную область определения
Х, хо
лежит внутри или является концом одного
из промежутков, образующих Х, и пусть
f(х) имеет предел в точке хо
равный L 0.
0.
Тогда
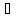 -окрестность
точки хо
такая, что на множестве {(хо-
-окрестность
точки хо
такая, что на множестве {(хо- ,
хо)}
,
хо)}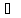 {(
хо,
хо+
{(
хо,
хо+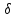 )}
)}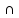 Х
функция f(х) имеет тот же знак, что и L.
Х
функция f(х) имеет тот же знак, что и L.
Доказательство.
Пусть
 f(х)=
L, L
f(х)=
L, L 0.
Возьмём
0.
Возьмём
 =
=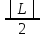 >0.
>0.
Тогда
 0,
а значит и для
0,
а значит и для
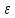 =
=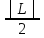 >0,
>0,
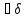 >0
>0
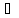 х
(
х
(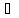 х
х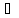 Х,
х
Х,
х хо,
хо, │x
- хо│<
│x
- хо│<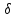 ):│
f(х)- L│<
):│
f(х)- L│<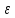 =
=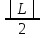
 L
L <f(х)<
L+
<f(х)<
L+
-
Пусть L>0
 │L│=L.
│L│=L.
Тогда х {(хо-
{(хо- ,
хо)}
,
хо)} {(
хо,
хо+
{(
хо,
хо+ )}
)} Х:
0<L-
Х:
0<L-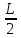 =
= <f(х)<
L+
<f(х)<
L+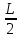
 0<
0<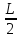 <f(х)
<f(х)
 f(х)>0.
f(х)>0.
-
Пусть L<0.
 │L│= - L.
│L│= - L.
 х
х {(хо-
{(хо-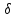 ,
хо)}
,
хо)}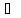 {(
хо,
хо+
{(
хо,
хо+ )}
)}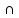 Х:
L+
Х:
L+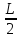 <f(х)<L-
<f(х)<L-

 L<
L<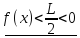
 f(х)<0
f(х)<0
Определение.
Функция f(х) называется ограниченной на множестве Х, если f(х) ограничена на Х и снизу, и сверху.
Теорема 7. (о локальной ограниченности функции, имеющей в точке предел).
Пусть
f(х) имеет стандартную область определения
Х, точка хо
лежит внутри
или является концом одного из промежутков,
образующих Х, и пусть f(х) имеет в точке
хо
предел, равный L. Тогда на множестве (хо
 хо+
хо+ )
)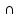 Х
f(х) ограничена.
Х
f(х) ограничена.
Доказательство.
 f(х)=
L
f(х)=
L
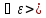 0,
а значит и для
0,
а значит и для
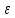 =1>0
=1>0
 >0
>0
 х
(
х
( х
х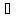 Х,
х
Х,
х хо,
хо, │x
- хо│<
│x
- хо│<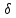 ):
│f(х)- L│<
):
│f(х)- L│<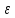 =1
=1
 L-1<f(х)<L+1
L-1<f(х)<L+1
а)
Пусть хо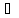 Х.
Х.
Положим A=min{L-1, f(хo)},
B=max{L+1, f(хo)}.
Тогда
 х
х (хо
(хо
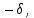 хо+
хо+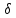 )
)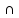 Х:
А
Х:
А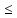 f(х)
f(х)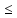 В.
В.
б)
хо Х.
Х.
Положим
 Тогда
Тогда
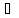 х
х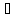 (хо
(хо
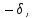 хо+
хо+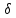 )
)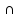 Х:
А
Х:
А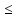 f(х)
f(х)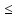 В
В
 f(х) ограничена.
f(х) ограничена.
