
- •Глава I. Действительные числа.
- •§1. Введение.
- •§2. Множества.
- •§3. Понятие множества действительных чисел.
- •§4. Отображения множеств.
- •Глава 2. Числовые последовательности.
- •§1. Понятие числовой последовательности.
- •§2. Бесконечно малые последовательности.
- •§3. Свойства сходящихся последовательностей.
- •Глава 3. Некоторые сведения из математической логики.
- •§1. Предложение.
- •§2. Предикаты.
- •§3. Кванторы.
- •§4. Предельный переход в неравенствах. (Глава 2)
- •§5. Бесконечно большие последовательности.
- •§6. Частичные последовательности (подпоследовательности).
- •§7. Монотонные последовательности.
- •§8. Теорема о вложенных отрезках.
- •§9. Теорема Больцано-Вейерштрасса.
- •§10. Критерий Коши сходимости числовой последовательности.
- •§11. Число .
- •Глава 3. Функции.
- •§1. Понятие числовой функции числового аргумента.
- •§2. Предел функции в точке.
- •§3. Арифметические свойства пределов функций.
- •§4. Предельный переход в неравенствах.
- •§5. Односторонние пределы функции в точке. (пределы слева и справа)
- •§6. Пределы функций на бесконечности.
- •§7. Функции, стремящиеся к бесконечности. (Бесконечно большие функции.)
- •§8. Сравнение бесконечно малых и бесконечно больших функций.
- •§9. Специальные пределы функций.
- •Глава 4. Непрерывность функции.
- •§1. Определение непрерывной функции.
- •§2. Классификация точек разрыва функции.
- •§3. Простейшие свойства непрерывных функций.
- •§4. Некоторые свойства непрерывных функций на промежутке.
- •§5. Условия непрерывности монотонной функции. Обратная функция. Непрерывность обратной функции.
- •Глава 5. Производная функции.
- •§1. Понятие производной функции.
- •§2. Свойства производной функции.
- •§3. Производная обратной функции.
- •§4. Таблица производных.
- •Глава 6. Дифференцируемая функция. Дифференциал.
- •§1. Понятие дифференцируемой функции в точке и дифференциала.
- •§2. Некоторые свойства дифференциала функции в точке.
§4. Некоторые свойства непрерывных функций на промежутке.
Теорема 1. (О промежуточных значениях непрерывной функции.)
Пусть f(x)
определена на промежутке X ненулевой
длины, и f(x)
непрерывна на X. Пусть a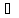 X,
b
X,
b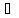 X
и a<b; f(a)=А, f(b)=В и А
X
и a<b; f(a)=А, f(b)=В и А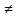 В.
В.
Тогда каково бы не было действительное число С, заключённое между А и В, на отрезке [a, b] существует точка с такая, что f(с)=С.
Доказательство.
I случай. Пусть А<0, В>0, С=0.
Докажем, что
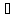 с
с [a,
b]: f(с)=0.
[a,
b]: f(с)=0.
Положим a1=a, b1=b.
f(a1)=А<0, f(b1)=В>0.
Разделим отрезок [a1, b1] пополам. Тогда возможны два случая:
либо f(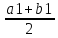 )=0
и с=
)=0
и с= ,
f(с)=0;
,
f(с)=0;
либо f(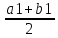 )
)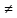 0
(f(
0
(f(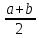 )
) 0).
0).
Если f(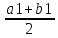 )>0,
то рассмотрим [a2,
b2]= [a1,
)>0,
то рассмотрим [a2,
b2]= [a1,
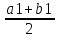 ],
если f(
],
если f(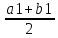 )<0,
то рассмотрим отрезок [a2,
b2]= [
)<0,
то рассмотрим отрезок [a2,
b2]= [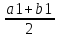 ,
a1]
,
a1]
 f(a2)<0, f(b2)>0.
f(a2)<0, f(b2)>0.
Разделим отрезок [a2,
b2] пополам. Тогда
либо f(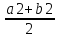 )=0
и теорема доказана; либо f(
)=0
и теорема доказана; либо f(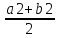 )
)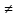 0
и мы возьмём так же, как и на первом шаге
отрезок [a3, b3]
0
и мы возьмём так же, как и на первом шаге
отрезок [a3, b3]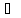 [a2,
b2]
[a2,
b2]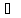 [a1,
b1], дл.[a3,
b3]=
[a1,
b1], дл.[a3,
b3]=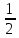 (b2–a2)=
(b2–a2)= дл.[a2,
b2], f(a3)<0,
f(b3)>0.
дл.[a2,
b2], f(a3)<0,
f(b3)>0.
Продолжим этот процесс. Тогда либо на
конечном шаге мы найдём нужную точку
с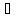 [a1,
b1]= [a,
b]: f(с)=0, либо мы построим
последовательность вложенных отрезков
[an,
bn]
таких, что
[a1,
b1]= [a,
b]: f(с)=0, либо мы построим
последовательность вложенных отрезков
[an,
bn]
таких, что
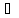 n:
дл.[an,
bn]=
n:
дл.[an,
bn]=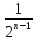 дл.[a1,
b1]=
дл.[a1,
b1]=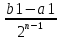 и f(an)<0, f(bn)>0.
и f(an)<0, f(bn)>0.
Тогда по теореме о вложенных отрезках
 an=
an=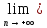 bn=с
bn=с

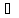 n:
с
n:
с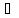 [an,
bn]
[an,
bn]
 с
с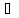 [a1,
b1]=
[a, b].
[a1,
b1]=
[a, b].
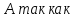 f(x) непрерывна на промежутке X, [a,
b]
f(x) непрерывна на промежутке X, [a,
b]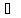 X,
то f(x) непрерывна на [a, b],
а, следовательно, и в точке с
X,
то f(x) непрерывна на [a, b],
а, следовательно, и в точке с

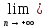 f(an)=
f(an)=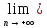 f(bn)=
f(с).
f(bn)=
f(с).
Но согласно
теореме о предельном переходе в
неравенствах для одной последовательности
f(an)<0
 f(с)
f(с)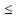 0
и f(bn)>0
0
и f(bn)>0
 f(с)
f(с)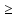 0
0
 f(с)=0.
f(с)=0.
II случай. Пусть А<В.
Докажем, что
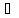 С:
А<С<В
С:
А<С<В
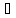 с
с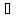 [a,
b]: f(с)=С.
[a,
b]: f(с)=С.
Рассмотрим функцию f1(x)= f(x) –С. Она непрерывна на X по теореме об арифметических свойствах непрерывных функций.
А–С= f(a) –С= f1(a)<0, f1(b)=В –С= f(b) –С>0.
Тогда
выполняются условия I-го случая

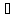 с
с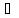 [a,
b]: f1(с)=0
[a,
b]: f1(с)=0
 f1(с)= f(с) –С=0
f1(с)= f(с) –С=0
 f(с)=С.
f(с)=С.
III случай. Пусть А>В.
Тогда
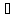 С:
В<С<А
С:
В<С<А
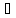 с
с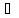 [a,
b]: f(с)=С.
[a,
b]: f(с)=С.
Рассмотрим функцию f2(x)= – f(x).
Из условия –В> –С> –А следует f2(a)= – f(a)= –А< –С< –В= f2(b)= – f(b).
f2(x) непрерывна на X, следовательно, и на [a, b]. Для неё выполняются условия случая II.
f2(a)=
–А, f2(b)= –В

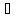 с
с [a,
b]: f2(с)= –С=–f(с)
[a,
b]: f2(с)= –С=–f(с)
 f(с)=С.
f(с)=С.
Замечание 1.
Теорема 1, в частности, верна и когда X=[a, b] и f(x) непрерывна на [a, b].
Замечание 2.
Для функции, заданной на стандартной области определения X, состоящей из нескольких промежутков, и непрерывной на X, теорема 1 применима к каждому промежутку отдельно.
Замечание 3.
Содержание
теоремы 1 кратко состоит в том, что если
X – промежуток и f(x) непрерывна на нём,
то область значения f(x) Y={y;
y= f(x), х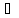 Х}
так же промежуток ( то есть непрерывная
функция отображает промежуток на
промежуток).
Х}
так же промежуток ( то есть непрерывная
функция отображает промежуток на
промежуток).
Теорема 2. (Первая теорема Вейерштрасса об ограниченности функции непрерывной на отрезке.)
Любая функция, непрерывная на отрезке, ограничена на нём.
Доказательство.
Пусть f(x) определена на [a, b], a<b. f(x) непрерывна на [a, b].
-
Докажем, что f(x) ограничена на [a, b] сверху

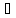 М
М
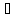 x
x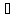 [a, b]: f(x)
[a, b]: f(x)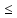 М.
М.
Предположим, что это не так, то есть
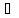 М
М
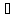 x´
x´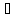 [a,
b]: f(x´)>М.
[a,
b]: f(x´)>М.
Тогда для М=1
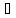 x1´
x1´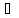 [a,
b]: f(x1´)>1
[a,
b]: f(x1´)>1
для М=2
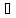 x2´
x2´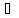 [a,
b]: f(x2´)>2
[a,
b]: f(x2´)>2
……………………………….
для М=n
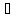 xn´
xn´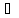 [a,
b]: f(xn´)>n
[a,
b]: f(xn´)>n
……………………………….
Мы построили последовательность {xn´}
такую, что
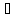 n:
xn´
n:
xn´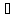 [a,
b], и {f(xn´)}
такова, что
[a,
b], и {f(xn´)}
такова, что
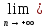 f(xn´)=+
f(xn´)=+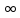 .
.
Проверим, что {f(xn´)}
стремится к +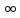 .
.
 f(xn´)=+
f(xn´)=+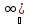
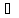 E>0
E>0
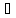 N
N
 n>N:
f(xn´)>E.
n>N:
f(xn´)>E.
Возьмём произвольное E>0 и зафиксируем
его. Тогда по аксиоме Архимеда
 N
– натуральное число такое, что N>E.
N
– натуральное число такое, что N>E.
Тогда
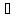 n>N:
f(xn´)>n>N>E
n>N:
f(xn´)>n>N>E

 n>N:
f(xn´)>E.
n>N:
f(xn´)>E.
А так как
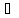 n:
xn´
n:
xn´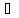 [a,
b], то {xn´}
ограничена, а тогда по теореме
Больцано-Вейерштрасса у неё существует
сходящаяся подпоследовательность
{xnk´}.
[a,
b], то {xn´}
ограничена, а тогда по теореме
Больцано-Вейерштрасса у неё существует
сходящаяся подпоследовательность
{xnk´}.
Пусть
 xnk´=с,
а так как
xnk´=с,
а так как
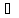 k:
a
k:
a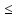 xnk´
xnk´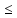 b,
то по теореме о предельном переходе в
неравенствах для одной последовательности
получаем a
b,
то по теореме о предельном переходе в
неравенствах для одной последовательности
получаем a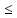 с
с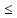 b
b
 с
с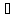 [a,
b].
[a,
b].
Но по условию теоремы f(x) непрерывна на
[a, b],
следовательно, и в точке с
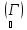
 f(xn´)=
f(с) и мы пришли к противоречию, так как
любая подпоследовательность
последовательности, стремящейся к +
f(xn´)=
f(с) и мы пришли к противоречию, так как
любая подпоследовательность
последовательности, стремящейся к +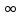 ,
стремится к +
,
стремится к +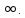
-
Пусть f(x) непрерывна на [a, b].
Докажем, что f(x) ограничена на [a,
b] снизу

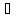 m
m
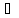 x
x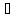 [a, b]: m
[a, b]: m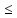 f(x).
f(x).
Рассмотрим функцию g(x)= –f(x). По
арифметическим свойствам непрерывной
функции, g(x) непрерывна на [a,
b] и по доказанному в п.1,
g(x) ограничена сверху на [a,
b], то есть
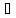 М
М
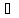 x
x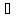 [a, b]: g(x)
[a, b]: g(x)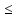 M,
ибо g(x)= –f(x)
M,
ибо g(x)= –f(x)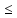 M
M
 f(x)
f(x)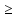 –M=m
–M=m

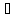 x
x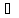 [a, b]: f(x)
[a, b]: f(x)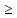 m.
m.
Следовательно, f(x) ограничена на [a,
b] и сверху и снизу
 f(x) ограничена на [a, b].
f(x) ограничена на [a, b].
Замечание 1.
Теорема 2 не распространяется на функции, непрерывные на промежутках другого вида.
Примеры.
-
f(x)=
 ,
X=(0, 1). f(x) непрерывна на (0, 1), но не
ограничена на интервале (0, 1) сверху.
,
X=(0, 1). f(x) непрерывна на (0, 1), но не
ограничена на интервале (0, 1) сверху. -
f(x)=x2, X=(–
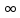 ,
+
,
+ ).
f(x) непрерывна на (–
).
f(x) непрерывна на (–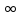 ,
+
,
+ ),
но не ограничена на (–
),
но не ограничена на (–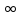 ,
+
,
+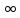 )
сверху.
)
сверху.
Замечание 2.
Если f(x) имеет
стандартную область определения X и
непрерывна на X, то теорема 2 применяется
к сужению непрерывной функции f(x) на
любом отрезке [a, b] X,
и эта функция сужения на [a,
b] ограничена на [a,
b].
X,
и эта функция сужения на [a,
b] ограничена на [a,
b].
Теорема 3.(Вторая теорема Вейерштрасса о достижении функцией, непрерывной на отрезке, своих точных граней.)
Любая функция, непрерывная на отрезке, достигает на нём своих точных, верхней и нижней, граней.
Доказательство.
Пусть f(x) непрерывна на отрезке [a, b], a<b. Тогда, согласно первой теореме Вейерштрасса, f(x) ограничена на [a, b].
А
тогда
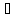 sup[a,
b] f(x)=Mo
и
sup[a,
b] f(x)=Mo
и
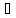 inf[a,
b] f(x)=mо.
inf[a,
b] f(x)=mо.
а) предположим,
что
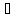 x
x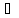 [a, b]:
[a, b]:
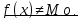
Тогда функция
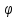 (x)=
(x)=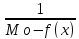 >0
и непрерывна на [a, b]
как частное двух непрерывных функций.
Согласно теореме 2,
>0
и непрерывна на [a, b]
как частное двух непрерывных функций.
Согласно теореме 2,
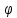 (x)
ограничена на [a, b]
(x)
ограничена на [a, b]

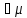 >0
>0
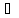 x
x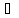 [a, b]: │
[a, b]: │ (x)│
(x)│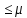
 0<
0<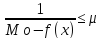
 Mo–f(x)
Mo–f(x)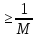

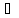 x
x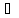 [a, b]: f(x)
[a, b]: f(x)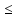 Mo–
Mo–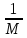 .
.
Это противоречит
тому, что Mo=
sup[a,
b]
f(x).(Вспомним,
что sup[a,
b] f(x)
– наименьшее из чисел, ограничивающих
множество значений функции на [a,
b] сверху.)

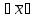 [a,
b]: f(
[a,
b]: f(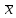 )=
Mo=
sup[a, b]
f(x).
)=
Mo=
sup[a, b]
f(x).
б)
Докажем, что
 [a,
b] такой, что
f(
[a,
b] такой, что
f(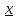 )=
mо=
inf[a, b]
f(x).
)=
mо=
inf[a, b]
f(x).
Для этого
рассмотрим функцию – f(x), x [a, b]. Она
непрерывна на [a, b],
и к ней применимо доказанное в п.а)
[a, b]. Она
непрерывна на [a, b],
и к ней применимо доказанное в п.а)

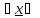 [a,
b]
[a,
b]
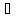 x
x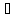 [a, b]: –
f(
[a, b]: –
f(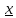 )
)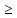 f(x)
f(x)
 x
x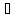 [a, b]:
f(
[a, b]:
f(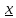 )
)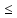 f(x),
то есть f(
f(x),
то есть f(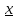 )=
inf[a,
b] f(x)=
mо.
)=
inf[a,
b] f(x)=
mо.
Замечание.
Теорема 3 неприменима к функциям, непрерывным на промежутках другого типа. Она применяется к сужению непрерывной функции на отрезке произвольном, целиком лежащем в области определения функции.
