
Понятие первообразной и неопределенного интеграла.
Замена переменных в определенном интеграле.
Интегрирование по частям.
Понятие сумм Дарбу и цель их введения.
Понятие определенного интеграла и их смысл.
Интегрируемость ограниченных функций(теорема существования)
Свойство линейности определенного интеграла.
Интеграл с переменным верхним пределом, его непрерывность и дифференцируемость.
Формула Лейбница-Ньютона.
Понятие несобственного интеграла.
Интегралы от неограниченных функций и по бесконечным промежуткам.
Гамма-функция.
Евклидово многомерное пространство.
Линейное пространство.
Неравенство треугольника.
Понятие внутренней и граничной множества точек.
Открытое и замкнутое множество.
Сходящиеся последовательности.
Критерий Коши сходимости последовательности.
Главная линейная часть приращения функции многих переменных.
Принцип суперпозиции.
Понятие дифференцируемости функций многих переменных.
Частные производные.
Полный дифференциал функций многих переменных. Условие экстремума функции.
Сложные функции и их дифференцирование.
Понятие производной по направлению.
Понятие градиента.
Касательная плоскость.
Частные производные высших порядков.
Неявные функции и их дифференцирование.
Задачи на условный экстремум.
Метод неопределенных множителей Лагранжа.
Понятие числового ряда и его сходимость.
Критерий Коши сходимости ряда.
Критерий сходимости Даламбера.
Условно сходящиеся ряды, теорема Римана об изменении суммы при смене порядка суммирования.
1. Определение: Функция F(x) называется первообразной для f(x) на [a,b], если в любой точке [a,b] F дифференцируема и выполняется соотношение: F’(x)=f(x).
Замечание: Если F(x) – первообразная для f(x) на заданном промежутке, то F(x) + C; C R – тоже первообразная.
Доказательство: F’(x) = f(x) – по условию
(F(x)+C)’ = F’(x)+0 = f(x)
Вывод: Если функция имеет первообразную, то она имеет их бесконечное множество.
Теорема. Все первообразные функции для f(x) отличаются на постоянную.
Доказательство: Пусть f(x) имеет F1(x) и F2(x), p(x) = F1(x) – F2(x); F1(x) и F2(x) дифференцируемы на ]a,b[ =>φ(x) тоже, при этом φ(x) = (F1(x) – F2(x))’ = F1’(x) – F2’(x) = f(x) – f(x) = 0. Но если производная равна нулю на[a,b], то φ(x) = С.
Определение: Множество всех первообразных для f(x) на ]a,b[ называется неопределённым интегралом от этой функции на ]a,b[. ∫f(x)dx; Таким образом, если F(x) задано первообразной f(x) на [a,b] то по определению: ∫f(x)dx = {F(x) + C, CR. Операция нахождения неопределённого интеграла от f(x) называется интегрированием f(x).
Свойства:
1) d∫f(x)dx = f(x)dx; d(F(x))=F’(x)dx =f(x)dx=d(∫f(x)dx);
2)∫dF(x)=F(x)+C; dF(x) =F’(x)dx=f(x)dx; ∫f(x)dx=F(x)+C;
3)∫(f(x) ±g(x))dx=∫f(x)dx+∫g(x)dx;
4)∫k*f(x)dx=k∫f(x)dx, k=const;
Табличные интегралы:
1) ∫0dx=c;
2) ∫1dx=∫dx=x+C;
3) ∫xαdx=(xα+1/α+1) + C (α≠-1)
4)
∫![]() =ln|x|+C
(x≠0)
=ln|x|+C
(x≠0)
5)∫axdx=![]() +C
(a≠1;a>0)
∫exdx=ex+C;
+C
(a≠1;a>0)
∫exdx=ex+C;
6)∫sinxdx=-cosx+C;
7)∫cosxdx=sinx+C;
8)∫![]() =tgx+C
(x≠
=tgx+C
(x≠![]() +πk)
+πk)
9)∫![]() =-ctgx+C
(x≠πk)
=-ctgx+C
(x≠πk)
10)∫![]() ={
={![]() (-1<x<1)
(-1<x<1)
11)∫![]() ={
={![]()
12)∫![]() =ln|x+
=ln|x+![]() |+C
|+C
13)∫![]() =
=![]() ln|
ln|![]() |+C
(|x|≠1);
|+C
(|x|≠1);
14)∫chxdx=shx+C
15)∫shxdx=chx+C
16)∫![]() =thx+C;
=thx+C;
17)∫![]() =-cthx+C
(x≠0)
=-cthx+C
(x≠0)
2).
Теорема: пусть 1)f(u); u=φ(x) определена на некотором промежутке. 2)Имеет смысл сложная функция f(φ(x)).
3)Функция φ(x)-дифференцируема, тогда если f(u) имеет первообразную, т.е. ∫f(u)dx=F(u)+C (1), то f(φ’(x)) имеет первообразную F(φ(x)) и => ∫f(φ(x))φ’(x)dx=F(φ(x))+C
Доказательство:F(u)
определена на том же интервале, что и
f(u).
По условию имеет смысл f(φ(x))
и значит F(φ(x)).
По правилу дифференцирования получим:
![]() F(φ(x))=
F(φ(x))=![]() =f(u)*
=f(u)*![]() |u=φ(x)=f(φ(x))φ’(x)
т.е. F(φ(x))
является первообразной для f’(φ(x))φ’(x).
∫f(u)|u=φ(x)=F(u)+C=F(φ(x))+C;
∫f(φ(x))φ’(x)dx=∫f(u)du
(3)
|u=φ(x)=f(φ(x))φ’(x)
т.е. F(φ(x))
является первообразной для f’(φ(x))φ’(x).
∫f(u)|u=φ(x)=F(u)+C=F(φ(x))+C;
∫f(φ(x))φ’(x)dx=∫f(u)du
(3)
3).
Теорема: если u(x)
и v(x)
дифференцируема на некотором промежутке
и![]() интеграл
∫vdu,
то также
∫udv,
причём ∫udv=uv-∫vdu.
интеграл
∫vdu,
то также
∫udv,
причём ∫udv=uv-∫vdu.
Доказательство: по правилу дифференцирования произведения d(uv)=vdu+udv и значит udv=(uv)-vdu. Ввиду равенства дифференциалов(производных) будут равны и интегралы. ∫udv=uv+∫vdu, т.к. ∫d(uv)=uv+C
4)
Пусть f(x)
ограничена на [a;b]
и T-разбиение
этого отрезка T:
a=x0<x1<…<xn<b.
Введём обозначение: Mi=sup(f(x));
m=inf(f(x))
на [xi-1;xi];
S=M1Δx1+…+MnΔxn=![]() -верхняя
сумма.
-верхняя
сумма.
s=m1Δx1+…+mnΔxn=![]() -
нижняя сумма.
-
нижняя сумма.
Свойства: 1)
![]() T:
s≤S
2)
σ
соответствующей T
s≤I
≤S;
mi≤f(ξi)≤Mi
T:
s≤S
2)
σ
соответствующей T
s≤I
≤S;
mi≤f(ξi)≤Mi
![]() ;
;
Свойства сумм Дарбу: 1) фиксированного разбиения Т и ε>0 промежуточные точки ξiє[xi-1;xi]:0≤S- σ(Т,ξi)<ε; 0≤ σ(Т,ξi)-s<ε;
Доказательство: пусть выполняется все перечисленные выше условия, т.к. Mi=supf(x), то по определению точной верхней грани будет выполняться: а) ε>0 ξiє[xi-1;xi]:f(ξ)≤Mi; б)
ε>0
ξiє[xi-1;xi]:f(ξi)>M-![]() ;
0≤ Mi-f(ξi)<
(i=1,2…,n).
Умножим
неравенство на Δxi
и просуммируем.
;
0≤ Mi-f(ξi)<
(i=1,2…,n).
Умножим
неравенство на Δxi
и просуммируем.
![]() ;
0≤ S-σ(Т,ξi)<ε.
Второе неравенство доказывается
аналогично.
;
0≤ S-σ(Т,ξi)<ε.
Второе неравенство доказывается
аналогично.
Следствие: если {σ(Т,ξi)} – множество всех интегральных сумм для f(x) и данного разбиения T отрезка [a;b], то s(T) = inf{σ(Т,ξi)}; S(T) = sup{ σ(Т,ξi)};
Доказательство: а) σє{σ(Т,ξi)}; σ≤S(T) б) согласно свойству 1) ε>0 σє{σ(Т,ξi)}; S-σ<ε или σ>S-є => S=sup{σ(Т,ξi)}; Второе утверждение доказывается аналогично.
2)Если разбиение Т’ полученное из Т путём добавления новых точек, то S(T’)≤S(T) или S’≤S; s(T)≤s(T’) или s≤s’
Доказательство:(для верхних сумм) достаточно к разбиению Т прибавить ещё одну точку x’, [x0;x1]; S=S*+M1(x1-x0); S’=S*+ M1’(x’-x0)+ M1’’(x1-x’); S-S’= M1(x1-x0)- M1’(x’-x0)- M1’’(x1-x’)=(M1-M1’)(x’-x0)+(M1-M1’’)(x1-x’); M1’≤M; M1’’≤M’; (точная верхняя грань на части отрезка не превосходит точной верхней грани на всём отрезке). Поэтому правая часть равенства больше нуля и s-s’≥0 => s’≤s. Для нижней суммы доказательство аналогично.
3)Пусть Т’ и T’’ - 2 разбиения [a;b], тогда справедливо неравенство: s(T’)≤S(T’’) и s’≤S’’; Любая нижняя сумма не превосходит верхнюю сумму.
Доказательство: для разбиений T’ и T’’ отрезка [a;b] T:T>T’ и T>T’’. Согласно свойству
2) имеем s(T’)≤s(T)≤S(T)≤S(T’’) и s’≤s≤S≤S’’
Следствие: множество {s} всех верхних сумм ограничено снизу любой нижней суммой, a {s} ограничено сверху любой верхней суммой.
Введём обозначение:
![]() =inf{S};
=inf{S};
![]() =sup{s};
=sup{s};
Определение: числа и называются верхним и нижним интегралом Дарбу. Из свойства 3) T: ≤ ; s≤ ≤ ≤S
5)
Определение определённого интеграла. Пусть на отрезке [a,b] задана функция y = f(x). Разобьём
отрезок [a,b] произвольным
образом на n частей
точками [x0 , x1],
[x1 , x2],
…, [xi-1
, xi],
…, [xn-1
, xn]; длину i-го
отрезка обозначим ![]() :
: ![]() ;
максимальную из длин отрезков обозначим
;
максимальную из длин отрезков обозначим ![]() .
На каждом из отрезков [xi-1
, xi] выберем
произвольную точку
.
На каждом из отрезков [xi-1
, xi] выберем
произвольную точку ![]() и
составим сумму
и
составим сумму 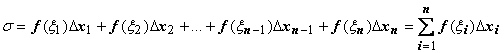 .
Определение.
Сумма
.
Определение.
Сумма ![]() называется
интегральной суммой.
Если существует (конечный) предел
последовательности интегральных
сумм
при
называется
интегральной суммой.
Если существует (конечный) предел
последовательности интегральных
сумм
при ![]() ,
не зависящий ни от способа разбиения
отрезка [a,b] на
части [xi-1
, xi],
ни от выбора точек
,
то функция f(x) называется
интегрируемой по отрезку [a,b],
а этот предел называется определённым
интегралом от
функции f(x) по
отрезку [a,b] и
обозначается
,
не зависящий ни от способа разбиения
отрезка [a,b] на
части [xi-1
, xi],
ни от выбора точек
,
то функция f(x) называется
интегрируемой по отрезку [a,b],
а этот предел называется определённым
интегралом от
функции f(x) по
отрезку [a,b] и
обозначается 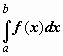 Функция f(x),
как и в случае неопределённого интеграла,
называется подынтегральной, числа a и b -
соответственно, нижним и верхним
пределами интегрирования.
Функция f(x),
как и в случае неопределённого интеграла,
называется подынтегральной, числа a и b -
соответственно, нижним и верхним
пределами интегрирования.
К ратко
определение иногда записывают так:
.
В
этом определении предполагается,
что b> a.
ратко
определение иногда записывают так:
.
В
этом определении предполагается,
что b> a.
Д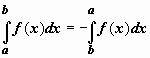 ля
других случаев примем, тоже по
определению:
Если b=a,
то
ля
других случаев примем, тоже по
определению:
Если b=a,
то 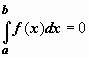 ;
если b<a,
то .
;
если b<a,
то .
Теорема существования определённого интеграла. Если функция f(x) непрерывна на отрезке [a,b], то она интегрируема по этому отрезку.
Геометрический
смысл определённого интеграла.
Как следует из пункта 11.1.1,
если f(x)
>0 на
отрезке [a,b], то 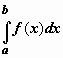 равен
площади криволинейной трапеции ABCD,
ограниченной снизу отрезком [a,b],
слева и справа - прямыми x = a и x = b,
сверху – функцией y =f(x).
равен
площади криволинейной трапеции ABCD,
ограниченной снизу отрезком [a,b],
слева и справа - прямыми x = a и x = b,
сверху – функцией y =f(x).
Формула
Ньютона-Лейбница. Если f(x) непрерывна
на отрезке [a, b],
и F(x) -
некоторая первообразная функции ![]() ,
то
,
то 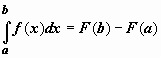
Формула
интегрирования по частям для определённого
интеграла. Если u(x), v(x) -
непрерывно дифференцируемые функции,
то 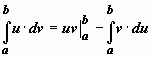
Замена
переменной в определённом интеграле. Теорема.
Пусть функция ![]()
определена,
непрерывно дифференцируема и монотонна
на отрезке ![]() ,
,
![]() ,
,
функция непрерывна на отрезке [a, b].
Тогда 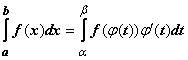 .
.
6)
Теорема: для
того, чтобы ограниченная на отрезке
функция была интегрируема на нём,
необходимо и достаточно, чтобы
![]() (1)
(1)
![]() ε>0
ε>0
![]() δ(ε)>0
T
δT<δ=>|S-s|<ε
δ(ε)>0
T
δT<δ=>|S-s|<ε
Примечание: S-верхняя, s-нижняя
