
- •Глава I. Действительные числа.
- •§1. Введение.
- •§2. Множества.
- •§3. Понятие множества действительных чисел.
- •§4. Отображения множеств.
- •Глава 2. Числовые последовательности.
- •§1. Понятие числовой последовательности.
- •§2. Бесконечно малые последовательности.
- •§3. Свойства сходящихся последовательностей.
- •Глава 3. Некоторые сведения из математической логики.
- •§1. Предложение.
- •§2. Предикаты.
- •§3. Кванторы.
- •§4. Предельный переход в неравенствах. (Глава 2)
- •§5. Бесконечно большие последовательности.
- •§6. Частичные последовательности (подпоследовательности).
- •§7. Монотонные последовательности.
- •§8. Теорема о вложенных отрезках.
- •§9. Теорема Больцано-Вейерштрасса.
- •§10. Критерий Коши сходимости числовой последовательности.
- •§11. Число .
- •Глава 3. Функции.
- •§1. Понятие числовой функции числового аргумента.
- •§2. Предел функции в точке.
- •§3. Арифметические свойства пределов функций.
- •§4. Предельный переход в неравенствах.
- •§5. Односторонние пределы функции в точке. (пределы слева и справа)
- •§6. Пределы функций на бесконечности.
- •§7. Функции, стремящиеся к бесконечности. (Бесконечно большие функции.)
- •§8. Сравнение бесконечно малых и бесконечно больших функций.
- •§9. Специальные пределы функций.
- •Глава 4. Непрерывность функции.
- •§1. Определение непрерывной функции.
- •§2. Классификация точек разрыва функции.
- •§3. Простейшие свойства непрерывных функций.
- •§4. Некоторые свойства непрерывных функций на промежутке.
- •§5. Условия непрерывности монотонной функции. Обратная функция. Непрерывность обратной функции.
- •Глава 5. Производная функции.
- •§1. Понятие производной функции.
- •§2. Свойства производной функции.
- •§3. Производная обратной функции.
- •§4. Таблица производных.
- •Глава 6. Дифференцируемая функция. Дифференциал.
- •§1. Понятие дифференцируемой функции в точке и дифференциала.
- •§2. Некоторые свойства дифференциала функции в точке.
Глава 3. Некоторые сведения из математической логики.
§1. Предложение.
-
Волга впадает в Балтийское море.
-
117<121
-
x отец y
-
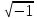 =i<3
=i<3 -
z исполнилось 17 лет
-
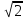 - рациональное число
- рациональное число -
 красного цвета
красного цвета
Определение.
Предложением называется высказывание, которое может быть истинным или ложным.
(1), (2), (3), (5), (6) – предложения. (часть из них истинны – (2), (3), (5); (1), (6) – ложны)
(4) и (7) не являются предложениями, так как они оба полностью бессмысленны, что не могут быть ни истинными, ни ложными, то есть лишены содержания.
Условимся обозначать предложения большими латинскими буквами А, В, С, … .
Вместе с каждым предложением А возникает предложение Ā - „не А”.
По определению считается, что Ā ложно (истинно) тогда, когда А истинно (ложно).
(1). Закон противоречия.
Ни при каком предложении А не могут быть А и Ā. Либо оба истинны, либо ложны.
-
Закон исключения третьего.
Для всякого предложения А оно само или его отрицание Ā истинно.
С точки зрения математической логики каждый закон физики и всякая теорема математики являются предложениями.
Над предложениями могут производится некоторые действия (операции).
Пусть задана упорядоченная пара предложений А и В.
Сложение.
Суммой
или дизъюнкцией
предложений А и В называется такое новое
предложение, обозначаемое А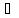 В,
которое читается „А или В”, причём А
В,
которое читается „А или В”, причём А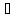 В
истинно, если
истинно
хотя бы одно из предложений А или В.
В
истинно, если
истинно
хотя бы одно из предложений А или В.
Умножение.
Определение.
Произведение
или конъюнкцией
двух предложений называется такое новое
предложение, которое обозначается А В
и читается „А и В”, причём А
В
и читается „А и В”, причём А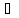 В
истинно,
когда каждое
из предложений и А
и В
истинны.
В
истинно,
когда каждое
из предложений и А
и В
истинны.
Импликация.
Определение.
Импликацией
предложений А и В называется такое новое
предложение, обозначаемое А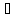 В,
которое читается следующим образом „из
А следует В”, или „если А то В”.
В,
которое читается следующим образом „из
А следует В”, или „если А то В”.
Причём
предложение А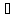 В
истинно во всех
случаях, кроме одного,
когда А – истинно, а В – ложно
В
истинно во всех
случаях, кроме одного,
когда А – истинно, а В – ложно
Пример.
А: n – кратно 4
В: n – чётно
Тогда
А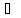 В.
В.
Эти введённые символы позволяют записать законы логики в простом виде:
-
А
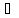 Ā – ложно при любом А.
Ā – ложно при любом А. -
А
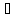 Ā
– истинно при любом А.
Ā
– истинно при любом А.
Импликация
в обе стороны, т.е. символ
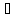 означает - равносильно.
означает - равносильно.
Для любых А, В, С:
-
А
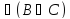
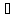 (А
(А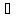 В)
В) (А
(А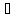 С)
С) -
А
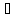 (В
(В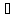 С)
С)
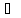 (А
(А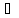 В)
В) (А
(А С)
С)
-
И (4) – распределительные законы.
Закон двойственности.
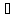
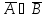
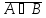
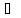
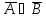
При определении отрицания предложениями и операций над предложениями важнейшим является согласование об истинности исходного предложения.
Таблица истинности.
|
А |
В |
Ā |
А V В |
А Л В |
А |
|
ист |
ист |
л |
ист |
ист |
ист |
|
ист |
л |
л |
ист |
л |
л |
|
л |
ист |
ист |
ист |
л |
ист |
|
л |
л |
ист |
л |
л |
ист |
Недоумение
может вызвать „ист” в нижнем правом
углу таблицы. Дело в том, что предложение
А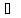 В
равносильно предложению
В
равносильно предложению
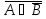
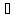 А
А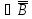

 В.
В.
Тогда
если А – ложно, то
 - истинно и дизъюнкция
- истинно и дизъюнкция
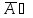 В
истинно.
В
истинно.
Таким образом, импликация беззащитна против ввода неверных данных.

 В
В