§3. Свойства сходящихся последовательностей.

Теорема 1.

Любая сходящаяся последовательность имеет единственный предел.

Доказательство. (от противного)

Пусть существует {x_n}, такая сходящаяся последовательность, для которой существуют два числа а и b, а<b , такие что

а=x_n, b=x_n, b>a.

так как a<b, то существуют непересекающиеся окрестности точек а и b.

Возьмём =(b-а)>0.

а=x_n для каждого >0, а значит и для =(b-а)>0 существует номер N₁ такой, что для любого n> N₁: │ x_n-а│<(b-а).

b=x_n для каждого >0, а значит и для =(b-а)>0 существует номер N₂ такой, что для любого номера n>N₂: │x_n-b│<(b-а).

Тогда для любого n>N=max{N₁, N₂} выполняются оба неравенства:

b- x_n<a+ b- a+ b-a<2=(b-а), что невозможно.

Мы пришли к противоречию.

Теорема 2.

Любая сходящаяся последовательность ограничена. Обратное неверно.

Доказательство.

I. Пусть {x_n} сходится. Докажем, что она ограничена.

{x_n} сходится существует число а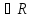 такое, что для каждого >0, а значит и для =1>0 существует номер N=N(1) такой, что для любого номера n>N:

│ x_n-а│<=1 а-1< x_n<а+1 x_n(а-1, а+1)

Положим А=min{x₁, x₂, …, x_N, a-1}

B=max{ x₁, x₂, …, x_N, a+1}

Тогда для любого n, n=1, 2, …: АВ.

II. Обратное неверно.

Рассмотрим последовательность 0, 1, 0, 1, …

Она ограничена числами 0 и 1.

Докажем, что она расходится. Для этого заметим, что если {x_n} сходится, то (x_n+1- x_n)=0. Действительно, возьмём произвольное >0 и зафиксируем его.

{x_n} сходится существует а такое, что для каждого >0, а значит и для нашего фиксированного >0 существует номер N такой, что для любого номера

n>N: │x_n-а│< а-< x_n<а+

n+1>N: │x_n+1-а│< а-< x_n+1<а+

Тогда │x_n+1- x_n│=│x_n+1-а- x_n+а│<= (x_n+1- x_n)=0.

Вернёмся теперь к последовательности 0, 1, 0, 1, …

n, n=1, 2, …: │x_n+1- x_n│=1 0, следовательно {x_n} расходится.

Арифметические свойства сходящихся последовательностей.

Теорема 3.

Пусть {x_n} и {y_n} две сходящиеся последовательности.

x_n=а, y_n=b.

Тогда {x_n+ y_n } сходится и её предел равен а+b.

Доказательство.

x_n=а для любого n: x_n=а+_n, где {_n} - б.м.

y_n=b для любого n: y_n=b+_n, где {_n} – б.м.

Тогда {x_n+y_n } сходится, т.к. n, n=1, 2, …: x_n+y_n=(а+_n)+(b+_n)=а+b+(_n+_n),

{_n+_n } – б.м., как сумма двух бесконечно малых последовательностей {_n} и{_n}.

Согласно лемме 2 §2 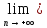(x_n+y_n)=а+b

Теорема 4.

Пусть {x_n} и {y_n} две сходящиеся последовательности, x_n=а, y_n=b.

Тогда {x_ny_n} сходится и её предел равен а∙b.

Доказательство.

x_n=а для каждого n: x_n=а+_n, где {_n} – б.м.

y_n=b для любого n: y_n=b+_n, где {_n} – б.м.

Тогда для любого n:

x_n y_n=(а+_n)∙(b+_n)=аb+а_n+b_n+_nn

Последовательности {_n} и {_n} бесконечно малые по лемме 1 §2, {_nn} – б.м., как произведение ограниченной на бесконечно малую по теореме 1§2 x_ny_n=а∙b.

Теорема 5.

Пусть {x_n} и {y_n} две сходящиеся последовательности, x_n=а, y_n=b, b0.

Тогда {} сходится и её предел равен .

Доказательство.

I. Пусть y_n=b, b.

Тогда последовательность {}: 1) имеет смысл

2) сходится

3) её предел равен

1) {} имеет смысл, то есть существует номер n_о такой, что для любого n_о: y_n, то есть {} определена.

В самом деле, т.к. y_n=b для каждого 0, а значит и для >0, существует номер N такой, что для любого номера n>N

│y_n-b│< b-<y_n<b+

Пусть b>0. │b│=b.

Тогда 0<b- ∙b=<y_n<∙b (*)

Пусть b<0. │b│= - b.

Тогда ∙b< y_n<∙b<0 (**).

Тогда для любого nN+1: y_n и {} опеределена.

2) Покажем, что {} ограничена.

Для любого n>N: либо 0<<y_n ││< ,

либо y_n< <0 ││< {} ограничена.

3) Докажем, что {} сходится и её предел равен .

Так как y_n=b для любого n: y_n=b+_n, где {_n} – б.м.

Пусть n_о: = = (b - y_n) = _n .

{_n } по лемме 3 §2 б.м., ибо {b- y_n }={-_n } – б.м.

А тогда = + - = +_n , {_n } б.м. и согласно теореме 1§2, = .

II. Докажем теперь, что{x_n∙}= {} сходится.

x_n=а, = .

Тогда по теореме 3 {} сходится и её предел равен .

Теорема 6.

Пусть {x_n} сходится и x_n=а.

Тогда {│x_n│} сходится и │x_n│=│а│.

Доказательство.

x_n=а для каждого >0 существует номер N такой, что для любого номера n>N: │x_n - а│<.

Возьмём произвольное >0, фиксируем его. Тогда

n>N: ││x_n│ - │а││ │x_n - а│< │x_n│=│а│.