
- •Глава I. Действительные числа.
- •§1. Введение.
- •§2. Множества.
- •§3. Понятие множества действительных чисел.
- •§4. Отображения множеств.
- •Глава 2. Числовые последовательности.
- •§1. Понятие числовой последовательности.
- •§2. Бесконечно малые последовательности.
- •§3. Свойства сходящихся последовательностей.
- •Глава 3. Некоторые сведения из математической логики.
- •§1. Предложение.
- •§2. Предикаты.
- •§3. Кванторы.
- •§4. Предельный переход в неравенствах. (Глава 2)
- •§5. Бесконечно большие последовательности.
- •§6. Частичные последовательности (подпоследовательности).
- •§7. Монотонные последовательности.
- •§8. Теорема о вложенных отрезках.
- •§9. Теорема Больцано-Вейерштрасса.
- •§10. Критерий Коши сходимости числовой последовательности.
- •§11. Число .
- •Глава 3. Функции.
- •§1. Понятие числовой функции числового аргумента.
- •§2. Предел функции в точке.
- •§3. Арифметические свойства пределов функций.
- •§4. Предельный переход в неравенствах.
- •§5. Односторонние пределы функции в точке. (пределы слева и справа)
- •§6. Пределы функций на бесконечности.
- •§7. Функции, стремящиеся к бесконечности. (Бесконечно большие функции.)
- •§8. Сравнение бесконечно малых и бесконечно больших функций.
- •§9. Специальные пределы функций.
- •Глава 4. Непрерывность функции.
- •§1. Определение непрерывной функции.
- •§2. Классификация точек разрыва функции.
- •§3. Простейшие свойства непрерывных функций.
- •§4. Некоторые свойства непрерывных функций на промежутке.
- •§5. Условия непрерывности монотонной функции. Обратная функция. Непрерывность обратной функции.
- •Глава 5. Производная функции.
- •§1. Понятие производной функции.
- •§2. Свойства производной функции.
- •§3. Производная обратной функции.
- •§4. Таблица производных.
- •Глава 6. Дифференцируемая функция. Дифференциал.
- •§1. Понятие дифференцируемой функции в точке и дифференциала.
- •§2. Некоторые свойства дифференциала функции в точке.
Глава 2. Числовые последовательности.
§1. Понятие числовой последовательности.
Рассмотрим
произвольное число a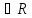 (а – фиксировано) и произвольное число
r
(а – фиксировано) и произвольное число
r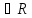 ,
r>0.
,
r>0.
Определение.
r-
окрестностью или окрестностью точки
а радиуса r называется
множество (а- r,
а+ r)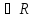 ,
где
,
где
(а-
r, а+ r)={x; x :
:
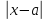 <r}={
x; x
<r}={
x; x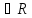 :
a-r<x<a+r}
:
a-r<x<a+r}
Что такое последовательность?
-
1, 1, 1, …, 1, …
-
1, 2, 3, …, n, …
-
-1, -2, -3, …, -n, …
-
0, 1, -1, 2, -2, …, k, -k, …
-
0, 1, 0, 1, …
-
1,
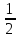 ,
,
 ,
…,
,
…,
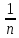 ,
…
,
… -
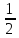 ,
0,
,
0,
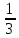 ,
0,
,
0,
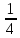 ,
0, …,
,
0, …,
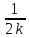 ,
0 ,
,
0 ,
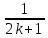 ,
…
,
… -
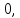 1, 0, 2, …, 0, k, 0, …
1, 0, 2, …, 0, k, 0, … -
 ,
,
 ,
,
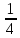 ,
,
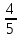 ,
…,
,
…,
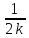 ,
,
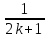 ,
…
,
… -
 ,
,
 ,
,
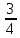 ,
…,
,
…,
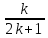 ,
…
,
…
Определение.
Говорят, что задана числовая последовательность, если указан закон, согласно которому каждому натуральному числу n поставлено в соответствие число xn.
Замечание.
Иногда полезно бывает допустить n=0, в других случаях целесообразно считать, что n принимает все положительные целые значения, начиная с nо, то есть n=nо, nо+1, nо+2, …, nо - целое, nо>0.
Будем обозначать последовательность
{x1, x2, …, xn, …}={ xn}
{ xn} или { xn}
или { xn}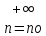
Определение.
Числовая
последовательность (1) называется
ограниченной сверху (снизу),
если существует число В такое, что для
любого n (n=1, 2, …): xn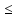 В
(соответственно существует число А
такое, что для любого n (n=1, 2, …): xn
В
(соответственно существует число А
такое, что для любого n (n=1, 2, …): xn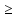 А).
А).
Определение.
Последовательность (1) называется ограниченной, если она ограничена и сверху и снизу.
Определение.
Числовая
последовательность (1) называется
возрастающей (убывающей), если
для любого n, n=1, 2, … : xn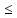 xn+1
(соответственно xn
xn+1
(соответственно xn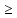 xn+1)
xn+1)
Определение.
Числовая последовательность (1) называется монотонной, если она либо возрастающая, либо убывающая.
Определение.
Последовательность (1) называется строго возрастающей (строго убывающей), если для любого n (n=1, 2, …): xn<xn+1 (соответственно xn>xn+1).
Общее название для строго возрастающей и строго убывающей последовательностей – строго монотонные.
Определение.
Число а
называется пределом последовательности
(1), если для каждого положительного
числа
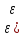 >0)
существует натуральное число (номер) N
такое, что для любого номера n>N:
>0)
существует натуральное число (номер) N
такое, что для любого номера n>N:
│xn-a│ или
-
или
-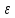 <
xn-а<
<
xn-а<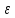
 а-
а-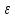 <
xn<
<
xn<
 xn
xn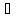 (а-
(а-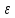 ,
а+
,
а+ )
)

(а где расположены x1, x2, …, xN?)
Предел
последовательности (1) обозначается:
а=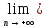 xn.
xn.
Определение.
Числовая
последовательность называется сходящейся,
если она имеет предел, то есть если
существует число а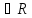 такое, что а=
такое, что а= xn
xn
 существует а
существует а такое, что для каждого
такое, что для каждого
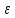 >0
существует номер N такой, что для каждого
номера n>N: │xn-a│
>0
существует номер N такой, что для каждого
номера n>N: │xn-a│ .
.
Определение.
Последовательность
(1) {xn
} называется расходящейся, если она
не имеет предела; если какое бы число
а не взять существует
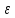 о
(
о
(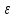 о>0)
такое, что для каждого номера N существует
номер nо>N такой, что │xno-a│
о>0)
такое, что для каждого номера N существует
номер nо>N такой, что │xno-a│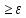 о.
о.
§2. Бесконечно малые последовательности.
Среди всех
сходящихся последовательностей
особую роль играют последовательности,
сходящиеся к нулю, то есть такие,
что 0=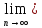 xn.
xn.
Определение.
0=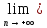 xn
xn
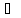 для каждого
для каждого
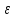 >0
существует номер N такой, что для каждого
номера n>N: │xn│<
>0
существует номер N такой, что для каждого
номера n>N: │xn│<
 xn
xn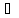 (-
(-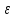 ,
,
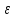 ).
).
Определение.
Последовательность, сходящаяся к нулю, называется бесконечно малой (б.м.).
Пример.
{1,
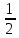 ,
,
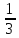 , …,
, …,
 , …}={
, …}={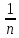 }
}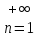
Докажем, что
 .
.
Возьмём
произвольное
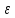 >0
и зафиксируем его. Ищем N такое, что для
любого номера n>N:
>0
и зафиксируем его. Ищем N такое, что для
любого номера n>N:
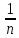 <
< .
.
Положим
N=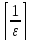 +1.
+1.
Возьмём
произвольный номер n>N=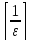 +1
+1
 n>
n>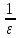
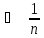 <
< .
Что и требовалось доказать.
.
Что и требовалось доказать.
Задача 1.
Пусть q – произвольной действительное число, │q│<1.
Рассмотрим
последовательность {1, q,
q2, …, qn,
…}={qn}
Доказать,
что
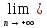 qn=0.
qn=0.
Задача 2.
Доказать, что любая бесконечная десятичная дробь является пределом последовательности своих десятичных приближений.
Теорема 1.
Для того,
чтобы последовательность (1) { xn}
сходилась к числу а необходимо и
достаточно, чтобы для любого номера
n, n=1, 2, …: xn=а+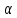 n,
где последовательность {
n,
где последовательность {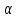 n}
б.м.
n}
б.м.
Доказательство.
-
Необходимость.
Пусть а=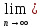 xn.
Рассмотрим последовательность {
xn.
Рассмотрим последовательность {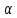 n}={
xn-а}.
n}={
xn-а}.
а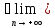 xn
для каждого
xn
для каждого
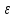 >0
существует номер N такой, что для любого
номера n>N: │xn-а│<
>0
существует номер N такой, что для любого
номера n>N: │xn-а│<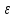
 │
│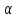 n│<
n│<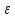
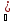 0=
0= n.
n.
-
Достаточность.
Пусть дана
последовательность { xn}
и для каждого n, n=1, 2, … : xn=а+ n,
где {
n,
где {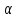 n}
– б.м.
n}
– б.м.
Докажем, что
а=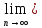 xn.
xn.
{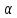 n}
– б.м.
n}
– б.м.
 для каждого
для каждого
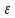 >0
существует номер N такой, что для каждого
номера n>N: │
>0
существует номер N такой, что для каждого
номера n>N: │ n│<
n│<
 │
│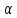 n│=│xn-а│<
n│=│xn-а│<
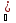 а=
а=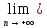 xn.
xn.
Свойства бесконечно малых последовательностей.
I Лемма 1.
Пусть { n}
б.м. Тогда для любого числа А
n}
б.м. Тогда для любого числа А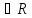 :
{
:
{ n}
– б.м.
n}
– б.м.
Доказательство.
-
А=0. Тогда для любого n, n=1, 2, …: А
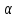 n=0
n=0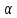 n=0
n=0
 {
{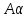 n}
– б.м.
n}
– б.м. -
{
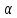 n}
- б.м.
n}
- б.м.
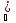 для каждого
для каждого
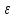 >0,
а значит для
>0,
а значит для
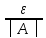 >0 существует номер N такой, что для
любого номера n>N:
>0 существует номер N такой, что для
любого номера n>N:
│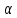 n│<
n│<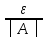
 │А│∙│
│А│∙│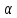 n│=│А
n│=│А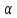 n│<
n│<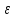
 0=
0= n
n
 {
{ n}
б.м.
n}
б.м.
II Лемма 2.
Сумма двух бесконечно малых последовательностей бесконечно мала.
Доказательство.
Пусть заданы
две б.м. последовательности {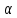 n}
и {
n}
и {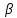 n}.
Рассмотрим последовательность {
n}.
Рассмотрим последовательность { n+
n+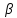 n
} и докажем, что она б.м.
n
} и докажем, что она б.м.
{ n}
– б.м.
n}
– б.м.
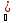 для каждого
для каждого
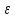 >0,
а значит и для
>0,
а значит и для
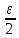 >0
существует номер N1 такой, что для
любого номера n>N1: │
>0
существует номер N1 такой, что для
любого номера n>N1: │ n│<
n│<
{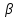 n}
– б.м.
n}
– б.м.
 для каждого
для каждого
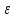 >0,
а значит и для
>0,
а значит и для
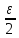 >0
существует номер N2 такой, что для
любого номера n>N2: │
>0
существует номер N2 такой, что для
любого номера n>N2: │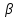 n
│<
n
│<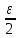 .
.
Тогда
 n>N=max{N1,
N2}: │
n>N=max{N1,
N2}: │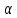 n+
n+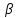 n│
n│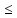 │
│ n
│+│
n
│+│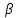 n
│<
n
│<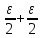 =
=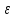

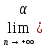 n+
n+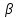 n)=0
n)=0
III Лемма 3.
Произведение б.м. последовательности на ограниченную последовательность – б.м.
Доказательство.
Пусть {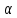 n}
– б.м., {
n}
– б.м., {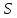 n}
ограничена. Докажем, что {
n}
ограничена. Докажем, что {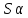 n}
– б.м.
n}
– б.м.
Так как {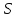 n}
ограничена
n}
ограничена существует
M>0 такое, что для любого n, n=1, 2, …:
│
существует
M>0 такое, что для любого n, n=1, 2, …:
│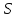 n│
n│ M.
M.
Если положить
А= -M, а В=M, то для любого n: А n
n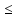 В
В
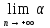 n=0
n=0
 для каждого
для каждого
 >0,
>0,
 >0
существует номер N такой, что для любого
номера n>N: │
>0
существует номер N такой, что для любого
номера n>N: │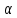 n│<
n│< .
.
Тогда для
любого номера n>N: │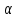 n∙
n∙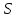 n│=│
n│=│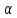 n│∙│
n│∙│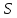 n│<
n│<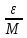 ∙M=
∙M=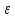 .
.
