
- •Глава I. Действительные числа.
- •§1. Введение.
- •§2. Множества.
- •§3. Понятие множества действительных чисел.
- •§4. Отображения множеств.
- •Глава 2. Числовые последовательности.
- •§1. Понятие числовой последовательности.
- •§2. Бесконечно малые последовательности.
- •§3. Свойства сходящихся последовательностей.
- •Глава 3. Некоторые сведения из математической логики.
- •§1. Предложение.
- •§2. Предикаты.
- •§3. Кванторы.
- •§4. Предельный переход в неравенствах. (Глава 2)
- •§5. Бесконечно большие последовательности.
- •§6. Частичные последовательности (подпоследовательности).
- •§7. Монотонные последовательности.
- •§8. Теорема о вложенных отрезках.
- •§9. Теорема Больцано-Вейерштрасса.
- •§10. Критерий Коши сходимости числовой последовательности.
- •§11. Число .
- •Глава 3. Функции.
- •§1. Понятие числовой функции числового аргумента.
- •§2. Предел функции в точке.
- •§3. Арифметические свойства пределов функций.
- •§4. Предельный переход в неравенствах.
- •§5. Односторонние пределы функции в точке. (пределы слева и справа)
- •§6. Пределы функций на бесконечности.
- •§7. Функции, стремящиеся к бесконечности. (Бесконечно большие функции.)
- •§8. Сравнение бесконечно малых и бесконечно больших функций.
- •§9. Специальные пределы функций.
- •Глава 4. Непрерывность функции.
- •§1. Определение непрерывной функции.
- •§2. Классификация точек разрыва функции.
- •§3. Простейшие свойства непрерывных функций.
- •§4. Некоторые свойства непрерывных функций на промежутке.
- •§5. Условия непрерывности монотонной функции. Обратная функция. Непрерывность обратной функции.
- •Глава 5. Производная функции.
- •§1. Понятие производной функции.
- •§2. Свойства производной функции.
- •§3. Производная обратной функции.
- •§4. Таблица производных.
- •Глава 6. Дифференцируемая функция. Дифференциал.
- •§1. Понятие дифференцируемой функции в точке и дифференциала.
- •§2. Некоторые свойства дифференциала функции в точке.
§3. Понятие множества действительных чисел.
Определение (аксиоматическое).
Непустое множество
 ={x}
элементов x произвольной природы
называется множеством действительных
чисел, если выполняются следующие
условия:
={x}
элементов x произвольной природы
называется множеством действительных
чисел, если выполняются следующие
условия:
I На множестве
 введена операция сложения элементов,
т.е. указан закон, согласно которому
каждой упорядоченной паре
элементов x, y из
введена операция сложения элементов,
т.е. указан закон, согласно которому
каждой упорядоченной паре
элементов x, y из
 поставлен в соответствие элемент из
поставлен в соответствие элемент из
 обозначаемый
x+y и называемый суммой
элементов x и y так, что
выполняются следующие (аксиомы сложения)
условия:
обозначаемый
x+y и называемый суммой
элементов x и y так, что
выполняются следующие (аксиомы сложения)
условия:
(1)I В
 существует единственный нейтральный
элемент (называемый нулём при сложении)
существует единственный нейтральный
элемент (называемый нулём при сложении)
 такой, что для любого x
такой, что для любого x выполнено:
выполнено:
x+ =
= +x=x
+x=x
(2)I Для каждого x существует единственный элемент из
существует единственный элемент из
 ,
называемый противоположным элементу
x, обозначаемый (-x) и такой, что
,
называемый противоположным элементу
x, обозначаемый (-x) и такой, что
x+(-x)=(-x)+x=
(3)I Для любых x,
y, z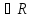
x+(y+z)=(x+y)+z (ассоциативность)
(4)I Для любых x,
y из

x+y=y+x (коммутативность)
II На множестве
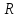 введена операция умножения элементов,
т.е. указан закон, согласовано которому
каждой упорядоченной паре
элементов x, y
из
введена операция умножения элементов,
т.е. указан закон, согласовано которому
каждой упорядоченной паре
элементов x, y
из
 поставлен в соответствие элемент из
поставлен в соответствие элемент из
 называемый произведением x
на y и обозначаемый xy
так, что выполнены следующие условия
(аксиомы умножения):
называемый произведением x
на y и обозначаемый xy
так, что выполнены следующие условия
(аксиомы умножения):
(1)II В
 существует единственный нейтральный
элемент (единица при умножении)
обозначаемый 1 такой, что для любого x
существует единственный нейтральный
элемент (единица при умножении)
обозначаемый 1 такой, что для любого x :
:
x·1=1·x=x
(2)II Для любого
x {
{ } существует единственный элемент из
} существует единственный элемент из
 ,
называемый обратным к x и обозначаемый
x-1 такой, что:
,
называемый обратным к x и обозначаемый
x-1 такой, что:
x· x-1= x-1·x=1
(3)II Для любых
x, y, z
из
 :
:
x·(y·z)=(x·y)·z (ассоциативность)
(4)II Для любых
x, y, z
из
 :
:
x·y=y·x (коммутативность)
(I, II) – Связь между сложением и умножением.
В
 для любых x, y,
z:
для любых x, y,
z:
(x+y)·z=x·z+y·z (дистрибутивность)
III На
 задано отношение порядка
задано отношение порядка ,
т.е. для любых двух элементов x,
y
,
т.е. для любых двух элементов x,
y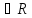 установлено: выполняется или нет
x
установлено: выполняется или нет
x (x меньше или равно
(x меньше или равно
 ).
).
При этом отношение
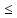 удовлетворяет следующим аксиомам
порядка:
удовлетворяет следующим аксиомам
порядка:
(1)III Для любого
x из
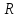 :
:
x (рефлексивность)
(рефлексивность)
(2)III Если для двух
x и y: x y
и y
y
и y x,
то x=y (x
есть y)
x,
то x=y (x
есть y)
(3)III Если для x,
y, z выполнено:
выполнено:
x y
и y
y
и y z,
то x
z,
то x z
(транзитивность)
z
(транзитивность)
(4)III Для любых x,
y, z ,
если x
,
если x y,
то
y,
то
x+z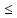 y+z
y+z
(5)III Для любых x,
y из
 ,
либо x
,
либо x y,
либо y
y,
либо y x
(либо и то и другое)
x
(либо и то и другое)
(6)III Для x,
y ,
если 0
,
если 0 x,
0
x,
0 y,
то 0
y,
то 0 xy
xy
Замечание.
-
По определению x
 означает, что y
означает, что y x.
x. -
Как следствие получаем, что для любых x, y
 имеет место одно и только одно из
соотношений:
имеет место одно и только одно из
соотношений:
x y,
x=y, x
y,
x=y, x y.
y.
IV Аксиома Архимеда.
Для любого
элемента с ,
удовлетворяющего условию 0
,
удовлетворяющего условию 0 с;
существует натуральное число n>с.
с;
существует натуральное число n>с.
V Аксиома полноты (непрерывности).
Для любых
двух непустых множеств X={x} и Y={y},
X , Y
, Y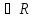 ,
удовлетворяющих условию: для любых x
,
удовлетворяющих условию: для любых x ,
y
,
y x
x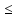 y,
существует элемент с
y,
существует элемент с такой, что для любого x
такой, что для любого x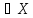 и любого y
и любого y :
x
:
x ,
с
,
с y,
т.е. x
y,
т.е. x y.
y.
Определение.
Каждый
элемент множества
 называется действительным числом.
называется действительным числом.
Приведённая система аксиом непротиворечива, т.к. существуют множества, удовлетворяющие I – V.
Например.
Десятичная форма числа, двоичная форма числа.
Замечание.
Единственность нейтральных элементов по сложению и умножению, а также противоположного и обратного элемента может быть выведена из аксиом и их единственность можно не требовать заранее.
Определение.
Непустое множество G, удовлетворяющее I: (1)I - (3)I называется аддитивной или абелевой4 группой.
Определение.
Непустое
множество
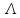 ,
удовлетворяющее условиям I(1-4),
II(1-4), (I,
II) называется полем.
,
удовлетворяющее условиям I(1-4),
II(1-4), (I,
II) называется полем.
Определение.
Непустое
множество
 ,
удовлетворяющее условиям называется
линейно упорядоченным полем.
,
удовлетворяющее условиям называется
линейно упорядоченным полем.
Определение.
Непустое множество, удовлетворяющее условиям I, II, III, IV называется архимедовым полем.
Определение.
Действительные числа 1, 1+1=2, 2+1=3, … называются натуральными числами.
Множество
 всех натуральных чисел содержит 1
и вместе с каждым n
всех натуральных чисел содержит 1
и вместе с каждым n содержит n+1.
содержит n+1.
Определение.
Все натуральные числа, все им противоположные и нуль образуют множество всех целых чисел.
Определение.
Число вида
p·q-1=
p· где
q
где
q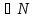 ,
p
,
p называется рациональным числом.
называется рациональным числом.
Множество
всех рациональных чисел обозначается
 .
.
Определение.
Каждое действительное число, не являющееся рациональным, называется иррациональным.
