
- •Глава I. Действительные числа.
- •§1. Введение.
- •§2. Множества.
- •§3. Понятие множества действительных чисел.
- •§4. Отображения множеств.
- •Глава 2. Числовые последовательности.
- •§1. Понятие числовой последовательности.
- •§2. Бесконечно малые последовательности.
- •§3. Свойства сходящихся последовательностей.
- •Глава 3. Некоторые сведения из математической логики.
- •§1. Предложение.
- •§2. Предикаты.
- •§3. Кванторы.
- •§4. Предельный переход в неравенствах. (Глава 2)
- •§5. Бесконечно большие последовательности.
- •§6. Частичные последовательности (подпоследовательности).
- •§7. Монотонные последовательности.
- •§8. Теорема о вложенных отрезках.
- •§9. Теорема Больцано-Вейерштрасса.
- •§10. Критерий Коши сходимости числовой последовательности.
- •§11. Число .
- •Глава 3. Функции.
- •§1. Понятие числовой функции числового аргумента.
- •§2. Предел функции в точке.
- •§3. Арифметические свойства пределов функций.
- •§4. Предельный переход в неравенствах.
- •§5. Односторонние пределы функции в точке. (пределы слева и справа)
- •§6. Пределы функций на бесконечности.
- •§7. Функции, стремящиеся к бесконечности. (Бесконечно большие функции.)
- •§8. Сравнение бесконечно малых и бесконечно больших функций.
- •§9. Специальные пределы функций.
- •Глава 4. Непрерывность функции.
- •§1. Определение непрерывной функции.
- •§2. Классификация точек разрыва функции.
- •§3. Простейшие свойства непрерывных функций.
- •§4. Некоторые свойства непрерывных функций на промежутке.
- •§5. Условия непрерывности монотонной функции. Обратная функция. Непрерывность обратной функции.
- •Глава 5. Производная функции.
- •§1. Понятие производной функции.
- •§2. Свойства производной функции.
- •§3. Производная обратной функции.
- •§4. Таблица производных.
- •Глава 6. Дифференцируемая функция. Дифференциал.
- •§1. Понятие дифференцируемой функции в точке и дифференциала.
- •§2. Некоторые свойства дифференциала функции в точке.
Глава 5. Производная функции.
§1. Понятие производной функции.
Пусть f(x) имеет стандартную область определения X, xо – внутренняя точка одного из промежутков X.Сместимся из точки xо в точку x= xо+∆x так, чтобы не покинуть X
x= xо+∆x X.
X.
Тогда f(x) получает приращение ∆f(xо, ∆x) в точке xо, вызванное смещением ∆x.
∆f=∆f(xо, ∆x)= f(xо +∆x) –f(xо)= f(x) – f(xо).
Пусть ∆x 0.
Рассмотрим
0.
Рассмотрим
 =
=
Определение.
Предел
 ,
если он существует, называется производной
функции f(x)
в точке xо и обозначается:
,
если он существует, называется производной
функции f(x)
в точке xо и обозначается:
f`(xо)=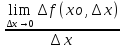 =
= =
= (x
(x xо)
xо) .
.
Теорема 1.
Пусть f(x)
имеет в точке x X
производную.
X
производную.
Тогда f(x) непрерывна в точке x.
Доказательство.
-
x
 X:
2.-3. Так как
X:
2.-3. Так как
 =
f`(x)
=
f`(x)

 =
f`(x)+
=
f`(x)+ (∆x),
где
(∆x),
где
 (∆x)=0.
(∆x)=0.
 f(x+∆x) –
f(x)= f`(x)·∆x+
f(x+∆x) –
f(x)= f`(x)·∆x+ (∆x)·
∆x
(∆x)·
∆x

 (f(x+∆x)
– f(x))=0
(f(x+∆x)
– f(x))=0

 f(x+∆x)=
f(x)
f(x+∆x)=
f(x)
 f(x) непрерывна
в точке x
f(x) непрерывна
в точке x X.
X.
§2. Свойства производной функции.
Пусть функции
f(x) и g(x)
имеют общую стандартную область
определения X, и во внутренней точке x
одного из промежутков X, x X
X
 f`(x)
и
f`(x)
и
 g`(x).
g`(x).
Тогда
(1).

x X,
X,
 f`(x), g`(x) по
условию, ∆x
f`(x), g`(x) по
условию, ∆x 0,
x+∆x
0,
x+∆x X
X
∆(f(x)+ g(x))=(f(x+∆x)+g(x+∆x)) – (f(x)+g(x))=(f(x+∆x) – f(x))+(g(x+∆x) – g(x))=∆f(x; ∆x)+∆g(x; ∆x)
(f(x)+
g(x))`= =
= (
( +
+ )=
f`(x)+ g`(x).
)=
f`(x)+ g`(x).
(2).

∆(f·g)=f(x+∆x)·g(x+∆x) – f(x)·g(x)=f(x+∆x)·g(x+∆x) – f(x)·g(x+∆x)+f(x)·g(x+∆x) –f(x)·g(x)=(f(x+∆x) –f(x))g(x+∆x)+f(x)(g(x+∆x) –g(x)).
Так
как
 (x)=
(x)=

 =
= (x)+
(x)+ (∆x)
(∆x)
 g(x+∆x) =g(x)+
g(x+∆x) =g(x)+ (x)·∆x+
(x)·∆x+ (∆x)·∆x
(∆x)·∆x

 g(x+∆x)=g(x)
g(x+∆x)=g(x)
 g(x) непрерывна в
точке x.
g(x) непрерывна в
точке x.
А значит,
 =
= (
( ·g(x+∆x)+f(x)·
·g(x+∆x)+f(x)· )=
f`(x)· g(x)+
f(x)·g`(x).
)=
f`(x)· g(x)+
f(x)·g`(x).
(3). Пусть
g(x) 0,
и по теореме о сохранении знака
непрерывной функции
0,
и по теореме о сохранении знака
непрерывной функции
 >0
>0
 ∆x:
x+∆x
∆x:
x+∆x (x
–
(x
– ,
x+
,
x+ )
) X:
g(x+∆x)
X:
g(x+∆x) 0.
0.
Тогда
 ∆x,
x+∆x
∆x,
x+∆x (x
–
(x
– ,
x+
,
x+ )
) X:
X:
∆ =
= –
–
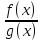 =
=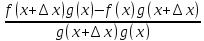 .
.
Возьмём ∆x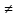 0
и рассмотрим
0
и рассмотрим
 =
=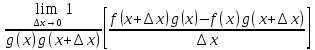

 f`(x)=
f`(x)= f(x+∆x)=
f(x)+
f`(x)·∆x+
f(x+∆x)=
f(x)+
f`(x)·∆x+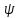 (∆x)·∆x,
где
(∆x)·∆x,
где
 (∆x)=0
(∆x)=0
 =
=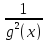 (f`(x)g(x)
– f(x)g`(x)).
(f`(x)g(x)
– f(x)g`(x)).
(3).

(4).
F(x)=f( (x)).
x
(x)).
x X,
x+∆x
X,
x+∆x X.
X.
∆F=F(x+∆x)
–F(x)=f( (x+∆x))
–f(
(x+∆x))
–f( (x)).
(x)).
f:
Z Y,
Y
Y,
Y R,
f(z) имеет
производную во внутренней точке z
R,
f(z) имеет
производную во внутренней точке z Z.
Z.
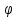 :
X
:
X ,
,
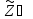 Z,
Z,
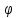 (x)
имеет производную во внутренней точке
x
(x)
имеет производную во внутренней точке
x X.
X.
Тогда

Доказательство.
Возьмём
произвольную внутреннюю точку x X
и сместимся из неё в точку x+∆x
X
и сместимся из неё в точку x+∆x X,
∆x
X,
∆x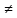 0
0
 ∆
∆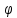 =∆
=∆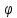 (x;
∆x)=
(x;
∆x)= (x+∆x)
(x+∆x) (x)=∆z
(x)=∆z
 f(z)получит приращение ∆f(z;
∆z)=f(z+∆z)
f(z)получит приращение ∆f(z;
∆z)=f(z+∆z) f(z)=f´(z)·∆z+
f(z)=f´(z)·∆z+ (∆z)·∆z
(∆z)·∆z
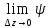 (∆z)=0,
ибо
(∆z)=0,
ибо
 f´(z)
f´(z)
 f´(z)(
f´(z)( (x+∆x)
(x+∆x) (x))+
(x))+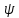 (∆z)·∆z.
(∆z)·∆z.
Делим на
∆x 0.
0.
 =
= =
= =f´(z)
=f´(z)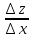 +
+ (∆z)
(∆z)

 =
f´(z)
=
f´(z) ´(x)+0=
f´(z)
´(x)+0=
f´(z) ´(x)
´(x)

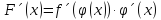 .
.
§3. Производная обратной функции.
Теорема.
Пусть функции
f: X Y
и g=f-1: Y
Y
и g=f-1: Y X
взаимно обратны и непрерывны в точках
xо
X
взаимно обратны и непрерывны в точках
xо X
и yо
X
и yо Y
соответственно; yо=f(xо). Если
f(x) имеет в точке xо производную и
f´(xо)
Y
соответственно; yо=f(xо). Если
f(x) имеет в точке xо производную и
f´(xо) 0,
то g(x) так же имеет производную в точке
yо= f(xо) и
0,
то g(x) так же имеет производную в точке
yо= f(xо) и
 .
.
Доказательство.
Так как f(x) и
g(x) взаимно обратны, то f(x) f(xо)
и g(y)
f(xо)
и g(y) g(yо) при y=f(x) не обращаются в нуль,
если x
g(yо) при y=f(x) не обращаются в нуль,
если x xо,
yо= f(xо).
xо,
yо= f(xо).
Из непрерывности
f(x) в точке xо и g(y) в точке yо
следует, что (x xо)
xо) (y
(y yо).
yо).
Используя
теорему о пределе сложной функции и
арифметические свойства пределов
функции, при ∆x 0,
∆y
0,
∆y 0
получаем
0
получаем
 =
= =
= =
= =
= .
.
Пример.
f(x)= ,
X=
,
X= .
.
X=g(y)=arcsin
y, y
 x
x
 y=sin x
y=sin x (
( 1,
1).
1,
1).
Применяя теорему о производной обратной функции, получаем
(arcsin
y)´=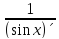 =
= =
= =
= .
.
§4. Таблица производных.
-
f(x)=
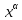 ,
X
,
X
Возьмём внутреннюю точку X, сместимся
из неё в точку x+∆x, не покидая X, x+∆x X
и пусть ∆x
X
и пусть ∆x 0.
0.
По определению f´(x)= .
.
Пусть x 0.
0.
f(x+∆x) f(x)=
f(x)=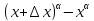 =
=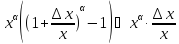 ·
· =
= ·
·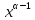 ·∆x
·∆x
 f´(x)=
f´(x)= =
= =
= ·
· .
.
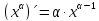 .
.
Пусть x=0,
 >1
>1
 =∆x.
=∆x.
 =
= =0
=0


 =1.
=1.
 <0
<0

 (либо точка x=0 не является внутренней,
либо нет производной).
(либо точка x=0 не является внутренней,
либо нет производной).
-
f(x)=
 ,
a>0, a
,
a>0, a 1,
X=(
1,
X=( ,
+
,
+ )
)
x X,
∆x
X,
∆x 0,
x+∆x
0,
x+∆x X.
X.
а) f(x)=
 =
=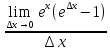 =
= =
= .
.
б) f(x)= =
= .
.
Применяя теорему о производной сложной
функции, получаем ( )´=(
)´=( )´=
)´= .
.

-
f(x)=
 ,
X=(0, +
,
X=(0, + ),
x
),
x X,
∆x
X,
∆x 0,
x+∆x
0,
x+∆x X.
X.
 =
= =
= =
= .
.

f(x)= ,
a>0, a
,
a>0, a 1,
X=(0, +
1,
X=(0, + ).
).
 =
=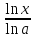


-
f(x)=
 ,
X=(
,
X=( ,
+
,
+ ),
∆x
),
∆x 0,
x+∆x
0,
x+∆x X.
X.
 =
= =
= =
= =
= =
= .
.

-
f(x)=
 ,
X=(
,
X=( ,
+
,
+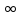 )
)
 =
= =
= =
= =
=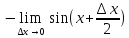 =
=

-
f(x)=tg x=

(tg x)´= =
= =
=

-
f(x) =ctg x=
 =
=
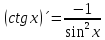
-
y= f(x)=
 ,
X=
,
X= ,
Y=[
,
Y=[ 1,
1]
1,
1]

Применяя теорему о производной обратной функции, получаем
( )´=
)´= =
= =
= =
= ,
x
,
x (
( ,
,
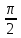 )
)
 y
y (
( 1,
1)
1,
1)

-
x=arcos y=
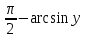 ,
y
,
y (
( 1,
1)
1,
1)

-
x=arctg y, Y=(
 ,
+
,
+ )
)
tg x=y
 (arctg y)´=
(arctg y)´= =
= =
= =
=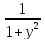

-
x=arcctg y, Y=(
 ,
+
,
+ )
)
(arcctg y)´= =
= =
= =
=

