
- •Глава I. Действительные числа.
- •§1. Введение.
- •§2. Множества.
- •§3. Понятие множества действительных чисел.
- •§4. Отображения множеств.
- •Глава 2. Числовые последовательности.
- •§1. Понятие числовой последовательности.
- •§2. Бесконечно малые последовательности.
- •§3. Свойства сходящихся последовательностей.
- •Глава 3. Некоторые сведения из математической логики.
- •§1. Предложение.
- •§2. Предикаты.
- •§3. Кванторы.
- •§4. Предельный переход в неравенствах. (Глава 2)
- •§5. Бесконечно большие последовательности.
- •§6. Частичные последовательности (подпоследовательности).
- •§7. Монотонные последовательности.
- •§8. Теорема о вложенных отрезках.
- •§9. Теорема Больцано-Вейерштрасса.
- •§10. Критерий Коши сходимости числовой последовательности.
- •§11. Число .
- •Глава 3. Функции.
- •§1. Понятие числовой функции числового аргумента.
- •§2. Предел функции в точке.
- •§3. Арифметические свойства пределов функций.
- •§4. Предельный переход в неравенствах.
- •§5. Односторонние пределы функции в точке. (пределы слева и справа)
- •§6. Пределы функций на бесконечности.
- •§7. Функции, стремящиеся к бесконечности. (Бесконечно большие функции.)
- •§8. Сравнение бесконечно малых и бесконечно больших функций.
- •§9. Специальные пределы функций.
- •Глава 4. Непрерывность функции.
- •§1. Определение непрерывной функции.
- •§2. Классификация точек разрыва функции.
- •§3. Простейшие свойства непрерывных функций.
- •§4. Некоторые свойства непрерывных функций на промежутке.
- •§5. Условия непрерывности монотонной функции. Обратная функция. Непрерывность обратной функции.
- •Глава 5. Производная функции.
- •§1. Понятие производной функции.
- •§2. Свойства производной функции.
- •§3. Производная обратной функции.
- •§4. Таблица производных.
- •Глава 6. Дифференцируемая функция. Дифференциал.
- •§1. Понятие дифференцируемой функции в точке и дифференциала.
- •§2. Некоторые свойства дифференциала функции в точке.
§2. Классификация точек разрыва функции.
Определение.
Точка разрыва xо функции f(x) называется точкой разрыва I-го рода, если
(А). xо X и xо лежит внутри
одного из промежутков, образующих X, и
в точке xо существуют односторонние
пределы функции f(x),
то есть
X и xо лежит внутри
одного из промежутков, образующих X, и
в точке xо существуют односторонние
пределы функции f(x),
то есть
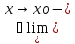 f(x)
и
f(x)
и
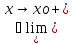 f(x).
f(x).
y
x
0
y
x



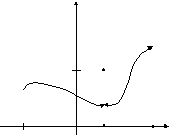
(В). xо X и является концом
только одного промежутка из X, и в
точке xо существует соответствующий
единственные односторонний предел
функции и он не равен значению f(xо).
X и является концом
только одного промежутка из X, и в
точке xо существует соответствующий
единственные односторонний предел
функции и он не равен значению f(xо).
(С). xо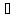 X, но является концом
одновременно двух смежных промежутков
из X и в точке xо
X, но является концом
одновременно двух смежных промежутков
из X и в точке xо
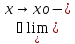 f(x)
и
f(x)
и
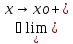 f(x).
f(x).
x y



x y


Определение.
Точка разрыва
I-го рода называется точкой устранимого
разрыва, если

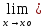 f(x).
f(x).
Слово устранимый означает, что можно взять такую функцию g(x), которая всюду совпадает с f(x), кроме точки xо, и g(x) непрерывна в точке xо.
Определение.
Любая точка разрыва, не являющаяся точкой разрыва I-го рода, называется точкой разрыва II-го рода.
Примеры.
-
f(x)=
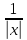 ,
(–
,
(– ,
0)
,
0) (0,
+
(0,
+ )
)
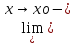 f(x)=+
f(x)=+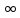 ,
,
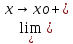 f(x)=+
f(x)=+

-
f(x)=
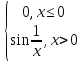 X=(
X=(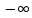 ,
+
,
+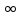 )
)
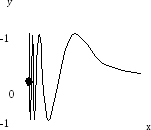
Точка xо=0 является точкой разрыва II-го рода.
Определение.
Говорят, что функция f(x) со стандартной областью определения X непрерывна справа (слева) в точке xо, если
-
xо
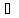 X
X -
 f(x)
(соотв.
f(x)
(соотв.
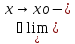 f(x)
)
f(x)
) -
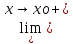 f(x)=
f(xо)
(соотв.
f(x)=
f(xо)
(соотв.
 f(x)=
f(xо)
)
f(x)=
f(xо)
)
§3. Простейшие свойства непрерывных функций.
Теорема 1. (Об арифметических свойствах непрерывных функций.)
Пусть функции f1(x) и f2(x) имеют общую стандартную область определения X, и обе эти функции непрерывны в точке xо.
Тогда в точке xо непрерывны и функции:
-
f1(x)
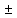 f2(x)
f2(x) -
f1(x)· f2(x)
-
Если f2(xо)
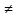 0,
то в точке xо непрерывна и функция
0,
то в точке xо непрерывна и функция
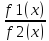
Доказательство.
Докажем
теорему 1 для функции f1(x) f2(x).
f2(x).
Функция f1(x)
определена на X1, f2(x)
определена на X2 и X=X1 X2.
X2.
Для функции
f1(x)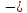 f2(x)
проверим выполнение всех трёх условий
непрерывности функции в точке xо.
f2(x)
проверим выполнение всех трёх условий
непрерывности функции в точке xо.
(1). xо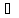 X.
X.
f1(x),
f2(x)
непрерывны в точке xо
 xо
xо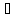 X1, xо
X1, xо X2
X2
 xо
xо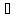 X.
X.
(2).





согласно арифметическим свойствам предела функции.
(3).
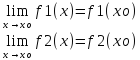

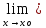 (f1(x)
(f1(x)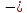 f2(x))=
f1(xо)
f2(x))=
f1(xо)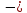 f2(xо)
f2(xо)
Все три
условия выполнены, следовательно,
функция f1(x) f2(x)
непрерывна в точке xо.
f2(x)
непрерывна в точке xо.
Определение.
Пусть f(z)
имеет стандартную область определения
Z, функция
 (x)
имеет стандартную область определения
X, и пусть
(x)
имеет стандартную область определения
X, и пусть
 x
x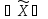 X:
X:
 (x)
(x) Z.
Z.
Тогда функция
F(x)=f(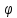 (x)),
определённая на
(x)),
определённая на
 ,
называется сложной функцией или
суперпозицией функций z=
,
называется сложной функцией или
суперпозицией функций z= (x)
и y=f(z).
(x)
и y=f(z).
Теорема 2. (О непрерывности сложной функции.)
Пусть функции
f(z),
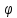 (x)
и F(x) имеют стандартные области определения
Z, X и
(x)
и F(x) имеют стандартные области определения
Z, X и
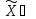 X
соответственно, и пусть f(z)
непрерывна в точке zо
X
соответственно, и пусть f(z)
непрерывна в точке zо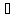 Z,
zо=
Z,
zо=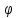 (xо),
(xо),
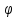 (x)
непрерывна в точке xо. Тогда F(x)
непрерывна в точке xо.
(x)
непрерывна в точке xо. Тогда F(x)
непрерывна в точке xо.
Доказательство.
Воспользуемся I-ой расшифровкой определения непрерывности.
F(x) непрерывна
в точке xо
 (1) xо
(1) xо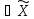
(2)-(3)
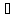 {хn}
{хn}
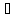 n:
хn
n:
хn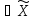 ,
,
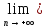 хn=
хо
:
хn=
хо
:
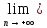 F(xn)=
F(xо) .
F(xn)=
F(xо) .
Возьмём
произвольную последовательность {хn}
такую, что
 n:
хn
n:
хn ,
,
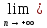 хn=
хо.
Тогда
хn=
хо.
Тогда
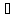 n:
n:
 (xn)=zn
(xn)=zn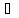 Z
и
Z
и
 zn=zо,
так как в силу непрерывности
zn=zо,
так как в силу непрерывности (x)
в точке xо
(x)
в точке xо
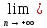 zn=
zn= (xn)=
(xn)=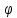 (xо)=
zо.
(xо)=
zо.
А так как
f(z) непрерывна в точке zо,
то
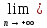 f(zn)=
f(zо)
f(zn)=
f(zо)

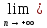 f(zn)=
f(zn)=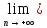 f(
f(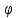 (xn))=f(
(xn))=f( (xо))
или
(xо))
или
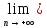 F(xn)=
F(xо).
F(xn)=
F(xо).
Теорема 3. (О сохранении знака непрерывной функции.)
Пусть f(x)
имеет стандартную область определения
X, f(x)
непрерывна в точке xо и пусть
f(xо) 0.
0.
Тогда
 -окрестность
(xо –
-окрестность
(xо –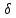 ,
xо+
,
xо+ )
точки xо такая, что на множестве
X
)
точки xо такая, что на множестве
X (xо
–
(xо
– ,
xо+
,
xо+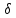 )
f(x) отлична
от нуля и имеет тот же знак, что и f(xо).
)
f(x) отлична
от нуля и имеет тот же знак, что и f(xо).
Доказательство.
f(x) непрерывна
в точке xо
 xо
xо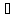 X
X
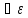 >0,
а значит и для
>0,
а значит и для
 >0
>0
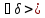 0
0
 x
(x
x
(x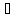 X, │x -
хо│<
X, │x -
хо│<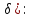 │f(x)
–f(xо)│<
│f(x)
–f(xо)│<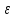 =
= f(xо)
–
f(xо)
–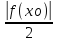 <f(x)<
f(xо)+
<f(x)<
f(xо)+ .
.
-
Пусть f(xо)>0
 │f(xо)│=
f(xо).
│f(xо)│=
f(xо).
Тогда
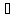 x
x (xо
–
(xо
–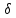 ,
xо+
,
xо+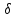 )
)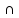 X:
f(xо)
–
X:
f(xо)
–
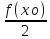 <f(x)<
f(xо)+
<f(x)<
f(xо)+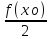

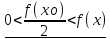 <
<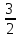 f(xо)
f(xо)

 x
x (xо
–
(xо
–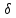 ,
xо+
,
xо+ )
)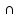 X:
f(x)>0.
X:
f(x)>0.
-
Пусть f(xо)<0
 │f(xо)│=
–f(xо).
│f(xо)│=
–f(xо).
 x
x (xо
–
(xо
– ,
xо+
,
xо+ )
) X:
f(xо)+
X:
f(xо)+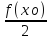 <f(x)<
f(xо)
–
<f(x)<
f(xо)
–
 <0
<0

 f(xо)<
f(x)<
f(xо)<
f(x)<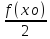 <0.
<0.
Теорема 4. (О локальной ограниченности непрерывной функции.)
Пусть f(x) имеет стандартную область определения X и непрерывна в точке xо.
Тогда существует такая окрестность точки xо, в которой f(x) ограничена.
Доказательство.
f(x)
непрерывна в точке xо
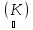 xо
xо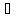 X,
X,
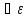 >0,
а значит и для
>0,
а значит и для
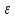 =1>0,
=1>0,
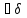 =
= (1)>0
(1)>0
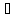 x
(x
x
(x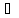 X, │x -
хо│<
X, │x -
хо│< ):
│f(x)
–f(xо)│<
):
│f(x)
–f(xо)│<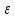 =1
=1
 f(xо)
–1<f(x)<
f(xо)+1.
f(xо)
–1<f(x)<
f(xо)+1.
Положим А=f(xо) –1, В=f(xо)+1.
Тогда
 x
x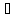 (xо
–
(xо
–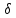 ,
xо+
,
xо+ )
)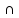 X:
А
X:
А f(x)
f(x)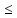 В
В
 f(x) ограничена
на множестве
f(x) ограничена
на множестве
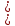 xо
–
xо
– ,
xо+
,
xо+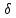 )
)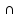 X.
X.
Множество
(xо –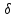 ,
xо+
,
xо+ )
) X
является окрестностью точки xо,
может быть и односторонней, так как X –
стандартная область определения.
X
является окрестностью точки xо,
может быть и односторонней, так как X –
стандартная область определения.
